Тема 1.2. Основные понятия теории вероятностей и статистики, применяемые в эконометрике (2 занятия)

1 Занятие

Вопросы для изучения

1. Основные понятия теории вероятностей. Нормальное распределение и связанные с ним 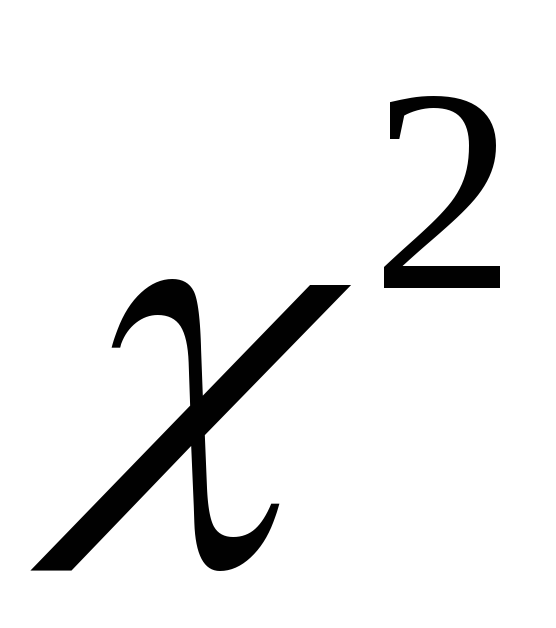- распределение, распределение Стьюдента и Фишера.

2. Генеральная совокупность и выборка. Статистическое оценивание. Свойства точечных оценок.

3. Интервальные оценки.

Контрольные вопросы

1. Приведите примеры случайных событий в экономике. Можно ли дать им вероятностное описание?

2. Перечислите основные свойства математического ожидания.

3. Перечислите основные свойства дисперсии.

4. Дайте определение ковариации.

5. Как определяется коррелированность и некоррелированность случайных величин?

6. Что такое генеральная совокупность и выборка?

7. Как вычисляются основные числовые характеристики по результатам выборки: выборочные среднее, дисперсия, среднее квадратическое отклонение?

8. Дайте определение несмещенности, эффективности и состоятельности.

9. Какие оценки называются наилучшими линейными несмещенными?

10. Что такое точечная и интервальная оценка?

Практические задания

Задача 1. Предполагается, что месячный доход граждан страны имеет нормальное распределение с математическим ожиданием =1000 $ и дисперсией40000. По выборке из 500 человек определили выборочный средний доход900 $.

Задание: следует ли на основании 95% доверительного интервала отклонить предложение о ежемесячном доходе в стране в 1000 $?

Задача 2. Взвешено 25 пакетов с чипсами, заполняемых автоматом, и найдено исправленное среднее квадратическое отклонение 1.

Задание: найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью0,95, если считать вес пакетанормально распределенной случайной величиной.

Задача 3. Вес продуктов измеряется прибором, систематическая ошибка которого равна нулю, а случайные ошибки распределены нормально со средним квадратическим отклонением =20 г.

Задание: сколько необходимо сделать независимых взвешиваний продукта, чтобы определить вес с ошибкой не более 15 г при доверительной вероятности 0,9?

Задача 4. На контрольных испытаниях 16 осветительных ламп были определены несмещенные оценки математического ожидания 3000 часов и среднего квадратического отклонения20 час их срока службы. Производитель ламп дает гарантию срока службы в 3100 часов. Срок службы каждой лампы является нормальной величиной.

Задание:

а) определите доверительный интервал для математического ожидания и среднего квадратического отклонения при доверительной вероятности 0,95;

б) можно ли по полученным данным доверять рекламе производителя?

Задача 5. На основе продолжительных наблюдений за весом пакетов орешков, заполняемых автоматом, установлено, что стандартное отклонение веса пакетов=10 г. Взвешено 25 пакетов и найден их средний вес244 г.

Задание: в каком интервале с надежностью 95% находится истинное значение среднего веса пакетов?

Задача 6. Обследование 25 человек показало, что их средний доход составил 1200 $ при среднем отклонении 120 $.

Задание: полагая, что доход имеет нормальный закон распределения, определить:

а) 95% интервальные оценки для математического ожидания и среднего квадратического отклонения;

б) вероятность того, что абсолютное значение ошибки оценивания не превзойдет 50 $;

с) количество обследованных, чтобы абсолютное значение ошибки оценивания не превзошло 50 $ с вероятностью 0,9.

Задача 7. Пусть ,- годовые дивиденды от вложений денежных средств в акции компаний А и В соответственно. Риск от вложений характеризуется дисперсиями25,16. Коэффициент корреляции=0,8.

Задание: что менее рискованно, вкладывать деньги в обе компании в соотношении 25% и 75% или только в компанию В?

Задача 8. Станок-автомат заполняет пакеты чипсами по 250 г. Считается, что станок требует подналадки, если стандартное отклонение от номинального веса превышает 5 г. Контрольное взвешивание 10 пакетов дало следующие результаты: 245, 248, 250, 250, 252, 256, 243, 251, 244, 253.

Задание: постройте 95 и 99% доверительные интервалы для стандартного отклонения от номинального веса.

Задача 9. На основании наблюдений за работой 25 кандидатов на должность секретаря-референта установлено, что в среднем они тратили 7 минут на набор одной страницы сложного текста на компьютере при выборочном стандартном отклонении S = 2 мин.

Задание:

1) определите 90 и 99% доверительные интервалы для мат. ожидания mx и среднего квадратического отклонения sx;

2) оцените количество претендентов на работу, которые набрали текст быстрее, чем за 5 минут.

3) не противоречат ли полученные данные предположению о том, что среднее время набора страницы должно составить 5 минут?

Задача 10. Обследование 25 человек показало, что их средний доход составил 1200$ при среднем отклонении S=120$. Доход имеет нормальный закон распределения.

Задание:

1) определите 90% интервальные оценки для мат. ожидания m и среднего квадратического отклонения s;

2) с какой вероятностью можно утверждать, что абсолютное значение ошибки оценивания m не превзойдет 50$;

3) каким должно быть количество обследованных, чтобы абсолютное значение ошибки оценивания m не превзошло 50$ с вероятностью 0,9?