Определение
Поверхность, которая в некоторой
декартовой системе координат задается
уравнением
называется эллиптическим цилиндром,
поверхность, заданная уравнением
называется гиперболическим цилиндром,
поверхность, заданная уравнением
,
называется параболическим цилиндром.
Для того чтобы построить поверхность,
задаваемую приведёнными уравнениями,
достаточно изобразить на плоскости
направляющую,
уравнение которой на этой плоскости
совпадает с уравнением самой поверхности,
и затем через точки направляющей провести
образующие параллельно оси
.
Для наглядности следует построить также
одно-два сечения плоскостями, параллельными
плоскости
.
В каждом таком сечении получим такую
же кривую, как и исходная направляющая.
Изображения этих цилиндров сечениями
приведены на рисунках 27,.29 и 31, а их
объемные изображения - на рисунках 28,
30 и 32.
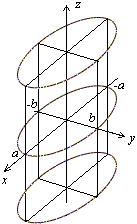
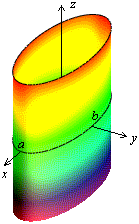
Рис.27.Изображение эллиптического цилиндра с помощью сечений Рис.28.Эллиптический цилиндр
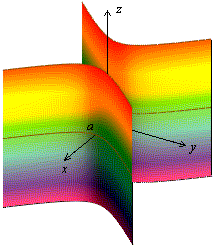
Рис.29.Изображение гиперболического цилиндра с помощью сечений Рис.30.Гиперболический цилиндр
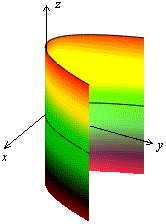
Рис.31.Изображение параболического цилиндра с помощью сечений Рис..32.Параболический цилиндр
Параллельный перенос системы координат
Так же как и на плоскости, в пространстве
можно выполнить параллельный перенос
системы координат. Пусть в пространстве
заданы две декартовы прямоугольные
системы координат: "старая" с
началом в точке
и осями
,
,
и
"новая" с началом в точке
и
осями
,
,
,
причем оси одной системы координат
соответственно параллельны осям другой
системы и одинаково с ними направлены.
Будем говорить, что вторая система
координат получена из первой параллельным
переносом.
Пусть начало
новой
системы координат имеет в старой системе
координаты
.
Пусть
-
некоторая точка пространства с
координатами
в
старой системе координат и
-
в новой системе координат. Тогда связь
между "старыми" и "новыми"
координатами точки
задается
формулами, аналогичными формулам
.
Пусть некоторая поверхность задана уравнением
Тогда в системе координат с началом в
точке
и
осями
,
,
,
полученной параллельным переносом,
уравнение поверхности будет иметь
вид
.
Пример 2. Построить поверхность
.
Решение. Выделим полные квадраты
по переменным
,
и
.
Введем новую систему координат с началом
в точке
,
получающуюся из старой параллельным
переносом. в новой системе поверхность
задается уравнением
Данное уравнение отличается от
канонического уравнения однополостного
гиперболоида тем, что поменялись ролями
оси ординат
и аппликат (
).
Не переобозначая осей, произведем
построение поверхности с помощью
сечений. В сечении плоскостью
получаем эллипс
Его полуоси равны 1 и 2 и лежат соответственно
на осях
и
.
В сечении плоскостью
получаем
гиперболу с уравнением
Ее мнимая ось лежит на оси
,
а действительная ось лежит на оси
,
полуоси соответственно равны 2 и 1. В
сечении плоскостью
получаем равностороннюю гиперболу
Ее мнимая ось лежит на оси
,
а действительная ось лежит на оси
,
обе полуоси равны 2. Для большей наглядности
нарисуем еще два сечения плоскостями
параллельными плоскости
.
В сечениях получим эллипсы, подобные
эллипсу в плоскости
.
По рассмотренным сечениям можно
представить себе форму гиперболоида и
его расположение в пространстве
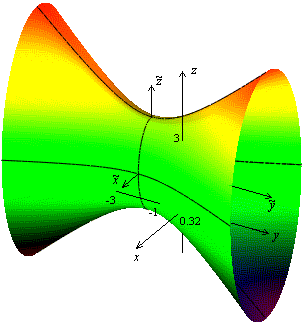
Рис. 33.Изображение поверхности с помощью сечений Рис. 34.Объемное изображение поверхности.