Определение.

Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид , где и - положительные числа.

Исследуем форму гиперболического параболоида. Так же, как и эллиптический параболоид, он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости , и координатная ось .

Для построения гиперболического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью . На этой плоскости , поэтому

.

Это уравнение определяет на плоскости пару прямых , изображенных на рис. 23.

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому .

Это уравнение на плоскости задает параболу, ветви которой направлены вниз. Построим ее (рис. 23). Сечение плоскостью также является параболой , но ее ветви направлены вверх (рис. 23).

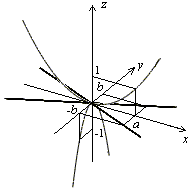
Рис.23.Сечения гиперболического параболоида координатными плоскостями

Найдем линии пересечения поверхности с плоскостью . Уравнения этой линии

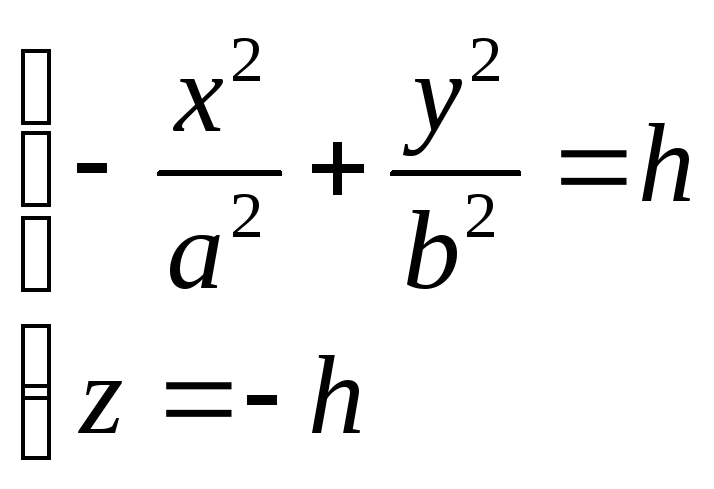
Первое уравнение преобразуем к виду , то есть к виду , где , . Данное уравнение является уравнением гиперболы. Ее действительная ось параллельна оси , а мнимая - оси . Полуоси равны соответственно и . Изобразим полученное сечение, но чтобы не перегружать рисунок линиями, асимптоты изображать не будем (рис. 24).

Найдем линии пересечения с плоскостями , параллельными плоскости . Уравнения этих линий

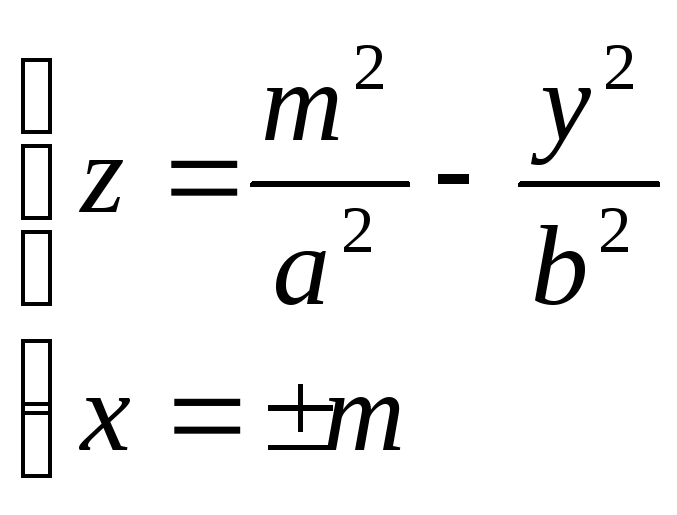
Первое из этих уравнений является уравнением параболы, такой же, как и в сечении плоскостью , только сдвинутой вдоль оси на величину вверх. Эти параболы изображены на рисунке 24.

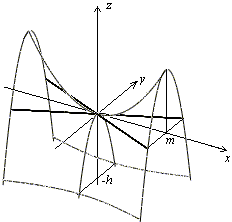
Рис.24.Изображение гиперболического параболоида с помощью сечений

Так как - произвольное число, то вся поверхность может быть получена движением параболы, лежащей в плоскости . Передвигать параболу нужно так, чтобы ее плоскость оставалась параллельной плоскости , а вершина скользила по параболе в плоскости .

Плоскость , , пересекает поверхность по гиперболе, но в отличие от гиперболы , ее действительная ось параллельна теперь оси , а мнимая -- оси (рис. 25).

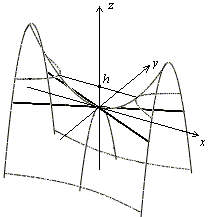
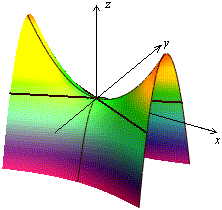
Рис.25.Дополнительное сечение Рис.26.Гиперболический параболоид

Цилиндры

Определение

Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые  образующими.

Рассмотрим уравнение вида . Покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси . Пусть  некоторая точка, координаты которой удовлетворяют уравнению. Поскольку в это уравнение не входит явно переменная , ему будут удовлетворять координаты всех точек , где - любое число. Следовательно, при любом точка лежит на поверхности, определяемой уравнением. Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку параллельно оси . А это означает, что поверхность, определяемая уравнением, составлена из прямых, параллельных оси , то есть она является цилиндрической поверхностью.

Заметим, что на плоскости уравнение определяет направляющую рассматриваемой цилиндрической поверхности.

Итак, делаем вывод, что если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.

Нас будут интересовать только те цилиндрические поверхности, которые являются поверхностями второго порядка.