Лекция 2.2

Алгебраической кривой второго порядка называется линия, уравнение которой в декартовой системе координат имеет вид , в котором А, В и С не могут быть одновременно равны нулю, т.е. .

1. Окружность и её уравнения.

Окружностью называется геометрическое место точек, равноудалённых от точки, называемой центром окружности.

Теорема Окружность радиуса Rс центром в точкеM_o(x₀,y₀₎ имеет уравнение (1)

Доказательство. Пусть - текущая точка окружности. По определению окружности расстояние равно R(рис.1)

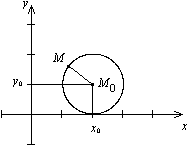
Рис. 1.Окружность

Выразив расстояние между точками получим

Обе части уравнения неотрицательны. Поэтому после возведения их в квадрат получим эквивалентное уравнение

Пример1 Определить координаты центра и радиус окружности .

Решение. Выделив полные квадраты, получим

Итак, центр окружности -- , радиус равен 2

Эллипс

Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.

В отличие от окружности, записать в "удобном" виде уравнение эллипса в произвольной системе координат не удается. Поэтому для фиксированного эллипса приходится подбирать систему координат так, чтобы его уравнение было достаточно простым.

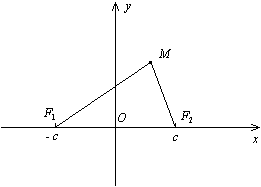
Пусть F₁ и F₂-- фокусы эллипса. Начало т.О системы координат расположим на середине отрезка . Ось направим вдоль этого отрезка, ось -- перпендикулярно к этому отрезку.

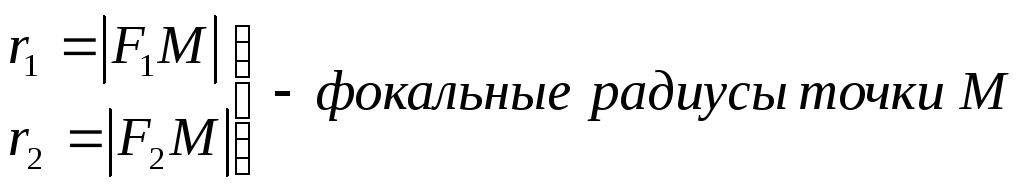
т. , т. ,

Тогда по определению эллипса

Перенесем один из корней вправо и обе части возведем в квадрат:

После того, как раскроем скобки и приведем подобные члены, приходим к выражению

Разделим обе части этого уравнения на 4 и возведем в квадрат

Раскроем скобку и приведем подобные члены

Учитывая, что , имеем равенство

Наконец, разделив обе части на , получим уравнение   (2)

Уравнение(2) называется каноническим уравнением эллипса.

Исследование полученного уравнения показывают:

• Эллипс имеет оси симметрии (Ох, Оу);

• начало координат- центр симметрии

Проведем построение эллипса, заданного уравнением (2). Заметим, что из-за симметрии достаточно нарисовать часть эллипса, лежащую в верхней полуплоскости. Уравнение этой линии мы получим, выразив у из уравнения (2) и взяв перед корнем знак "+",

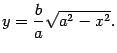
Построим график этой функции. Область определения - отрезок , y(0) = b, при увеличении переменного от 0 до функция монотонно убывает. В силу симметрии графика относительно оси функция y монотонно растет при изменении от –a до 0. Производная определена во всех точках интервала и, следовательно, график является гладким (не содержит изломов, касательная есть в любой точке). Вторая производная отрицательна во всех точках интервала , следовательно, график - выпуклый вверх.

Осталось не исследованным поведение кривой вблизи концов отрезка . Выразим из уравнения (2) переменное через y: . Очевидно, что в точке y = 0 эта функция имеет производную, то есть касательная к этому графику в точке существует. Легко проверить, что она параллельна оси Oy. Из симметрии эллипса делаем вывод, что это гладкая кривая и строим ее с учетом полученных данных (рис. 3).

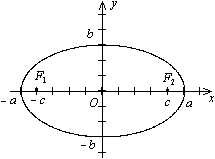
Рис.3.Эллипс

Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины - большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины - малой полуосью. . Величина , являющаяся половиной расстояния между фокусами, определяется из формулы (12.5) для величины , а именно, (3).

Величина называется эксцентриситетом эллипса. Эксцентриситет эллипса характеризует степень вытянутости эллипса. Чем ближе эксцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса .

Пример 2 Постройте кривую . Найдите фокусы и эксцентриситет.

Решение. Разделим обе части уравнения на 36. Получаем уравнение

Это - каноническое уравнение эллипса, , . Делаем чертеж (рис. 4)

Рис.4.Эллипс, заданный уравнением

Из соотношения (3) находим , . Фокусы - , , эксцентриситет - .

Пример 3   Построить эллипс . Найти его фокусы и эксцентриситет.

Решение. Уравнение запишем в виде

Это уравнение не является каноническим уравнением эллипса, так как в соответствии с уравнением (2) в нем , , , а должно быть . Однако, если переобозначить оси, то есть положить , , то уравнение (2) в координатах примет вид

Это -- каноническое уравнение эллипса при , . Делаем чертеж (рис. 5).

Рис.12.8.Эллипс, заданный уравнением

Из соотношения (3) находим . Значит, фокусы в системе координат имеют координаты , , а в системе координат - координаты, . Эксцентриситет равен .

Из примера 3 ясно, что построение кривой (эллипса) с уравнением (2) при можно вести так же, как и для эллипса, заданного каноническим уравнением: отложить полуось на оси , полуось  - на оси Оу и через получившиеся вершины провести эллипс. Различие заключается в том, что фокусы теперь располагаются на оси ординат (большой оси), величину нужно вычислять по формуле , и .