
Лекция 2. Матрицы и действия над ними
1. Матрицы. Операции над матрицами.
Матрицей размера mn называется прямоугольная таблица, состоящая из элементов некоторого множества (чисел, функций), имеющая m строк и n столбцов.
Положение каждого элемента в матрице однозначно определяется номером строки и номером столбца, на пересечении которых он находится.
Условно матрица может обозначаться следующим образом:
А =
 или
или
![]()
где i - номер строки, j - номер столбца на пересечении которых находится элементы матрицы aij.
-
Матрицу называют квадратной, если m = n.
-
Матрица размера
 содержит только одну строку
содержит только одну строку
 и называется матрицей – строкой.
и называется матрицей – строкой. -
Матрица размера
 содержит только один столбец и
называется матрицей – столбцом.
содержит только один столбец и
называется матрицей – столбцом. -
Матрицу, состоящую из одного элемента, отождествляют с этим элементом
 .
. -
Матрица, все элементы которой равны «0», называется нулевой (выраженной).
-
Квадратная матрица порядка n вида
 называется диагональной.
называется диагональной. -
Если в диагональной матрице
 ,
то эта матрица называется единичной
,
то эта матрица называется единичной
 .
.
Квадратной матрице порядка n можно поставить в соответствие её определитель (детерминант). Он представляет собой определитель n – ого порядка, составленный из тех же элементов, что и матрица.
А =


Операции над матрицами.
-
Две матрицы
 и
и
 называются равными, если их размеры
совпадают и равны их соответствующие
элементы:
называются равными, если их размеры
совпадают и равны их соответствующие
элементы:
 .
. -
Сложение матриц: С = А+В. ! Сложить можно только матрицы одного размера. Суммой двух матриц
 и
и
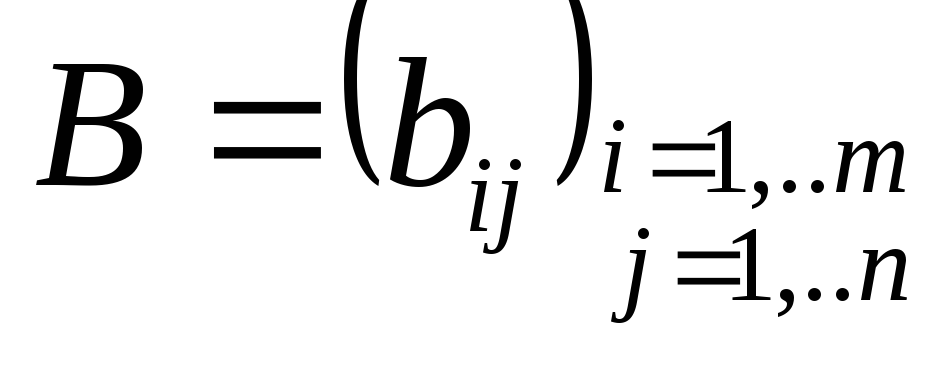 называют матрицу
называют матрицу
 того же размера, что и матрицы А и В,
элементы которой
того же размера, что и матрицы А и В,
элементы которой
 .
Свойства:
1) А + В = В + А;
2) (А + В) + С = А
+ (В + С).
.
Свойства:
1) А + В = В + А;
2) (А + В) + С = А
+ (В + С).
-
Умножение матрицы на число: Произведением матрицы
 на число
на число
 называется матрица , элементы которой
называется матрица , элементы которой
 .
Свойства:
1)
.
Свойства:
1)
 (А
+ В) =
(А
+ В) =
 В
+
В
+
 А;
2)
А;
2)
 ;
3)
;
3)
 .
. -
Умножение матриц ! Умножение матрицы А на матрицу В возможно только тогда, когда число столбцов матрицы А равно числу строк матрицы В. Если матрицы квадратные, то они должны иметь одинаковый порядок. Произведением матрицы
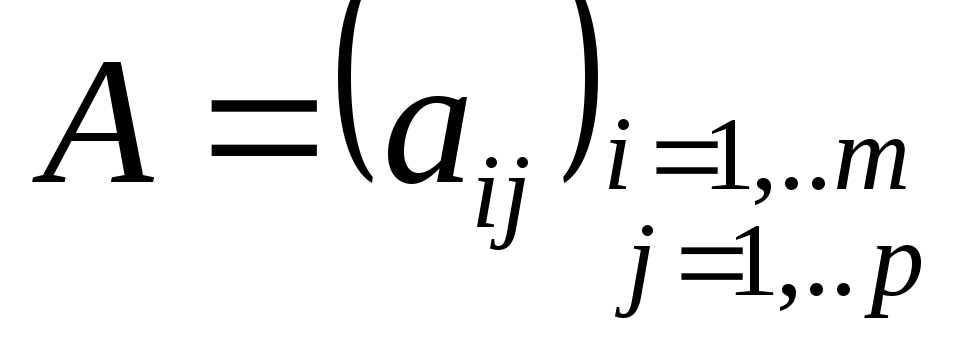 на матрицу
на матрицу
 называется матрица
называется матрица
 ,
элементы которой
,
элементы которой
 ,
где
,
где
 .
Свойства:
1)
в общем случае
.
Свойства:
1)
в общем случае
 ;
2)
;
2)
 ;
3)
;
3)
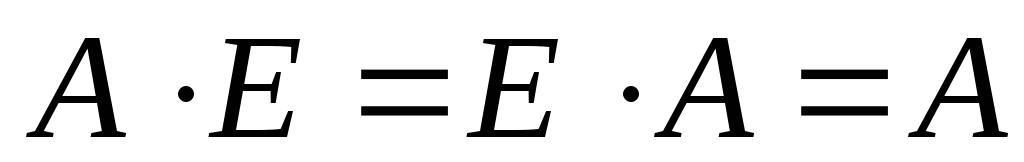 ;
4)
;
4) ;
5)
;
5) ;
6)
;
6)
 .
. -
Транспонирование матрицы Транспонированием матрицы называется замена строк этой матрицы её столбцами с сохранением номеров, т.е.
 .
Свойства:
1)
.
Свойства:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 .
. -
Обратная матрица Если A – квадратная невырожденная (
 )
матрица, то существует матрица B
такая, что
)
матрица, то существует матрица B
такая, что
 ,
которая называется обратной относительно
A и обозначается
,
которая называется обратной относительно
A и обозначается

 .
.
Для нахождения обратной матрицы необходимо:
-
построить вспомогательную матрицу
 ,
сформированную из алгебраических
дополнений к элементам матрицы А:
,
сформированную из алгебраических
дополнений к элементам матрицы А:

 ;
; -
транспонировать
 ;
; -
разделить каждый элемент матрицы на detA.
-
Степень квадратной матрицы Всякую квадратную матрицу А можно умножить саму на себя, т.е. найти матрицу
 .
Эта матрица называется квадратом
матрицы и обозначается
.
Эта матрица называется квадратом
матрицы и обозначается
 .
Аналогично,
.
Аналогично,
 .
Исходная
матрица А называется матрицей первой
степени
.
Исходная
матрица А называется матрицей первой
степени
 .
Нулевой
степенью матрицы А называется единичная
матрица Е, т.е.
.
Нулевой
степенью матрицы А называется единичная
матрица Е, т.е.
 .
Целая
отрицательная степень матрицы А
определяется как
.
Целая
отрицательная степень матрицы А
определяется как
 ,
где n>0
Свойства: 1)
,
где n>0
Свойства: 1)
 ;
2)
;
2)

-
Элементарные преобразования матрицы Элементарными преобразованиями матрицы называют следующие операции: 1) умножение всех элементов некоторой строки матрицы на число
 ;
2)
перемена местами строк матрицы;
3)
прибавление к какой-либо строке линейной
комбинации других строк.
Если матрица
В получена из матрицы А элементарными
преобразованиями, то матрицы А и В
называются эквивалентными
;
2)
перемена местами строк матрицы;
3)
прибавление к какой-либо строке линейной
комбинации других строк.
Если матрица
В получена из матрицы А элементарными
преобразованиями, то матрицы А и В
называются эквивалентными
 .
С помощью элементарных преобразований
матрицу приводят к ступенчатому виду,
когда все элементы, лежащие ниже главной
диагонали равны «0».
.
С помощью элементарных преобразований
матрицу приводят к ступенчатому виду,
когда все элементы, лежащие ниже главной
диагонали равны «0». -
Ранг матрицы Рассмотрим матрицу А размера
 . Выберем в этой матрице произвольно k
строк и k столбцов, где
. Выберем в этой матрице произвольно k
строк и k столбцов, где
 .
Составим определители k-ого
порядка. Все такие определители называют
минорами k-ого
порядка матрицы А.
Пример. Из матрицы
.
Составим определители k-ого
порядка. Все такие определители называют
минорами k-ого
порядка матрицы А.
Пример. Из матрицы
 можно составить 12 миноров 1-ого порядка
– это сами элементы матрицы А.
Если
выбрать какие-либо две строки и два
столбца матрицы, то получим миноры
2-ого порядка, например
можно составить 12 миноров 1-ого порядка
– это сами элементы матрицы А.
Если
выбрать какие-либо две строки и два
столбца матрицы, то получим миноры
2-ого порядка, например
 .
Минорами
3-его порядка являются определители
.
Минорами
3-его порядка являются определители
 =0,
=0,
 =0,
=0,
 =0,
=0,
 =0.
Все определители 3-его порядка равны
«0», среди миноров 2-ого порядка есть
неравные «0».
Если у матрицы все миноры
порядка
=0.
Все определители 3-его порядка равны
«0», среди миноров 2-ого порядка есть
неравные «0».
Если у матрицы все миноры
порядка
 равны «0», а среди миноров порядка n
имеется хотя бы один, отличный от «0»,
то число r называется
рангом матрицы и обозначается
равны «0», а среди миноров порядка n
имеется хотя бы один, отличный от «0»,
то число r называется
рангом матрицы и обозначается
 Вычисление
ранга матрицы перебором всех её миноров
очень трудоёмко. С помощью элементарных
преобразований матрицу приводят к
ступенчатому виду, когда все элементы,
расположенных ниже главной диагонали
равны «0».
!Ранг исходной матрицы
будет равен числу ненулевых строк
преобразованной матрицы.
Пример.
Вычисление
ранга матрицы перебором всех её миноров
очень трудоёмко. С помощью элементарных
преобразований матрицу приводят к
ступенчатому виду, когда все элементы,
расположенных ниже главной диагонали
равны «0».
!Ранг исходной матрицы
будет равен числу ненулевых строк
преобразованной матрицы.
Пример.
 ,
следовательно,
,
следовательно,
 .
.
Матричный способ решения систем линейных уравнений
Рассмотрим систему из n линейных уравнений с n неизвестными:
 или
или
![]()
![]() - неизвестное, подлежащее определению;
- неизвестное, подлежащее определению;
![]() - коэффициенты при неизвестных;
- коэффициенты при неизвестных;
![]() - свободные члены системы уравнений.
- свободные члены системы уравнений.
Решением системы называется совокупность
таких значений
![]() ,
которые обращают все уравнения системы
в тождество.
,
которые обращают все уравнения системы
в тождество.
Если система имеет хотя бы одно решение, то она называется совместной. В противном случае она называется несовместной.
Две системы линейных уравнений называются эквивалентными, если любое решение каждой из них является одновременно решением и другой системы.
Матричная запись системы
Составим из коэффициентов при неизвестных
матрицу А =
 - матрица системы. Введём ещё две матрицы:
- матрица системы. Введём ещё две матрицы:
 ,
,
 .
.
Тогда систему можно представить в
матричном виде
![]() .
.
Т.к
![]() ,
таким образом,
,
таким образом,
![]() .
.
Критерий совместности системы (теорема Кронекера-Капелли)
Для того, чтобы система линейных уравнений
была совместна, необходимо и достаточно
чтобы ранги основной и расширенной
матриц были одинаковы, т.е.
![]() ,
где
,
где
![]() - расширенная матрица системы. Она
получается из матрицы А добавлением к
ней столбца свободных членов:
- расширенная матрица системы. Она
получается из матрицы А добавлением к
ней столбца свободных членов:
![]()
 .
.
Следствия:
-
если
 (
( ),
где n – число
неизвестных, то система имеет единственное
решение;
),
где n – число
неизвестных, то система имеет единственное
решение;
-
если
 ,
то система имеет бесчисленное множество
решений, при этом
,
то система имеет бесчисленное множество
решений, при этом
 ,
r неизвестных
являются основными (базисными), а
остальные n-r
– свободными;
,
r неизвестных
являются основными (базисными), а
остальные n-r
– свободными; -
 ,
то система несовместна.
,
то система несовместна.
Решение систем линейных уравнений методом Гаусса (метод исключения неизвестных)
Рассмотрим систему
![]() ,
где А – матрица размера
,
где А – матрица размера
![]() .
.
Элементарными преобразованиями приведём
расширенную матрицу
![]() этой системы к ступенчатому виду. При
этом возможны три случая:
этой системы к ступенчатому виду. При
этом возможны три случая:
-
система получилась в виде:
 .
Начиная с последней строки, двигаясь
к первой, находим последовательно
.
Начиная с последней строки, двигаясь
к первой, находим последовательно
 .
Решение системы будет единственное.
Этот случай соответствует
.
Решение системы будет единственное.
Этот случай соответствует
 .
. -
система получилась в виде:
 .
Неизвестные
.
Неизвестные
 переносим в правую часть и считаем их
свободными
переносим в правую часть и считаем их
свободными
 Далее,
начиная с последней строки, находим
неизвестные
Далее,
начиная с последней строки, находим
неизвестные
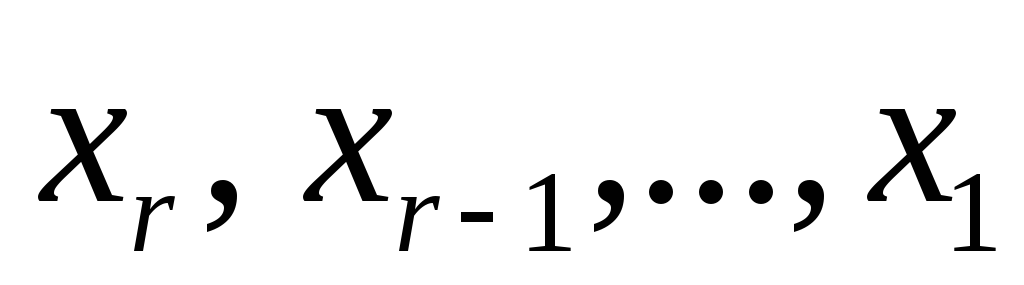 ,
выраженные через свободные неизвестные
,
выраженные через свободные неизвестные
 .
Решений
системы бесчисленное множество. Этот
случай соответствует
.
Решений
системы бесчисленное множество. Этот
случай соответствует
 .
. -
Система получилась в виде:
 ,
,
 - система не совместна. Этот случай
соответствует
- система не совместна. Этот случай
соответствует
 .
.
Пример 1. Установить совместность
и решить систему:
 .
.
Решение:
В расширенной матрице системы поменяем
1-ю и 2-ю строки для того, чтобы элемент
![]() был равен «1».
был равен «1».

![]() ~
~

![]() ~
~

![]() ~
~

![]() ~
~
~

![]() ~
~

![]() ~
~

![]()
Имеем
![]() .
Ранги матрицы системы и её расширенной
матрицы совпали с числом неизвестных.
Согласно теореме Кронекера -Капелли
система уравнений совместна и решение
её единственно. Запишем расширенную
матрицу в виде системы уравнений:
.
Ранги матрицы системы и её расширенной
матрицы совпали с числом неизвестных.
Согласно теореме Кронекера -Капелли
система уравнений совместна и решение
её единственно. Запишем расширенную
матрицу в виде системы уравнений:
 ,
следовательно
,
следовательно
 .
.
