Модуль1. Векторная и линейная алгебра

Лекция 1-1 Определители и их свойства. Решение систем линейных уравнений методом Крамера.

1. Определители и их свойства.

Определителем порядка «n» называется число, полученное по определённому правилу.

В общем виде определитель представляется в виде таблицы nn и обозначается «∆» или det.

Определителем второго порядка называется выражение:

∆ = ,

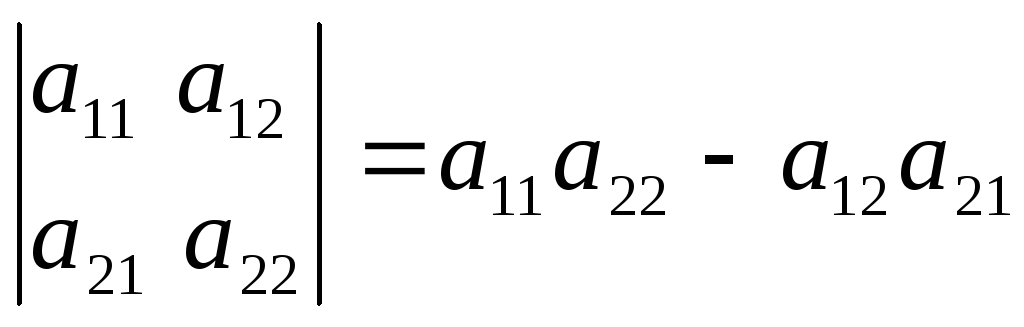где числа - элементы определителя.

Определитель второго порядка равен разности произведений его элементов главной и побочной диагоналей.

Пример1.

∆ = ,

Определитель третьего порядка (n = 3) можно вычислить по правилу Саррюса

∆ = ,

Пример 2.

∆ = ,

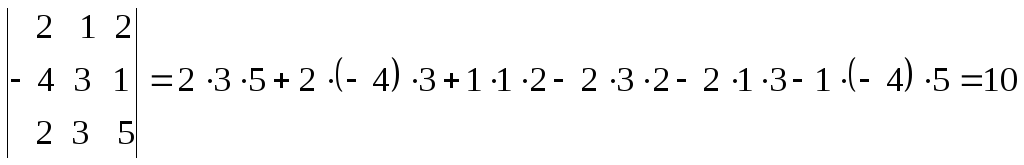• Суммой нескольких строк определителя называется строка, каждый элемент которой равен сумме соответствующих элементов этих строк.

• Произведением строки на число называется строка, каждый элемент которой равен произведению соответствующего элемента этой строки на данное число.

• Линейной комбинацией нескольких строк определителя называется строка, равная сумме произведений соответствующих элементов этих строк на некоторые числа.

• Минором 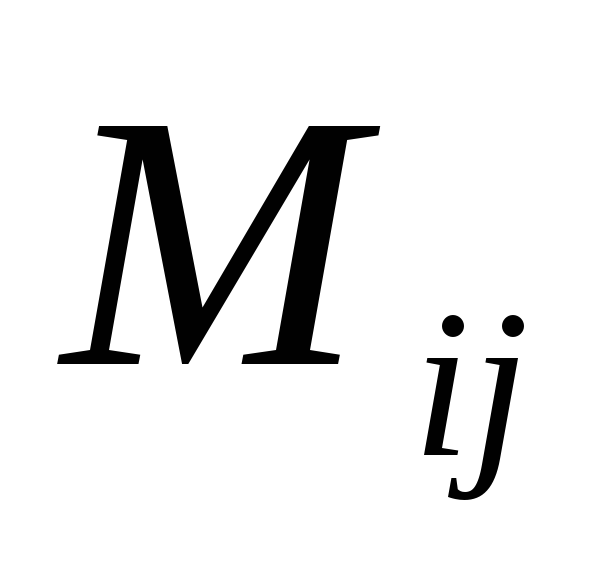элемента определителя порядка «n» называется определитель порядка «n-1», полученный из определителя порядка «n» вычёркиванием строки с номером «i» и столбца с номером «j» на пересечении которых находится данный элемент.

• Алгебраическим дополнением данного элемента определителя называется минор этого элемента, взятый со знаком 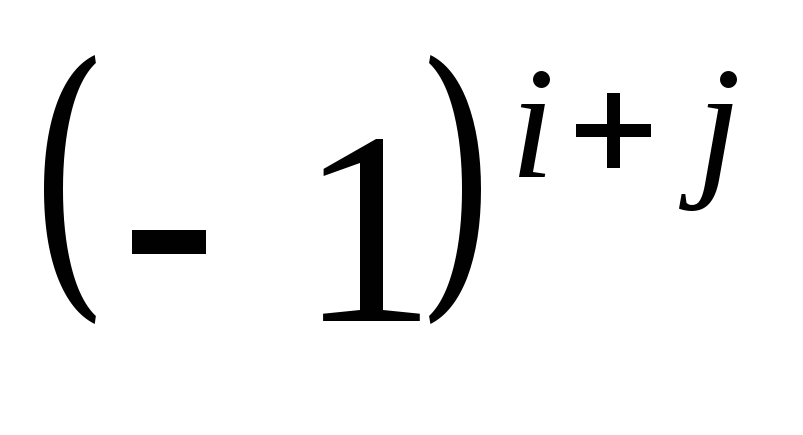, где i, j – номера строки и столбца на пересечении которых находится данный элемент

• Используя введённое понятие, сформулируем основное правило вычисления определителе – правило Лапласа:

Определитель равен сумме произведений элементов любой его строки (столбца) на соответствующие им алгебраические дополнения

.

2. Свойства определителей

   1. Если поменять местами строки и столбцы определителя, не меняя их порядка (транспонируя определитель), то определитель не изменит своё значение ∆ = ,

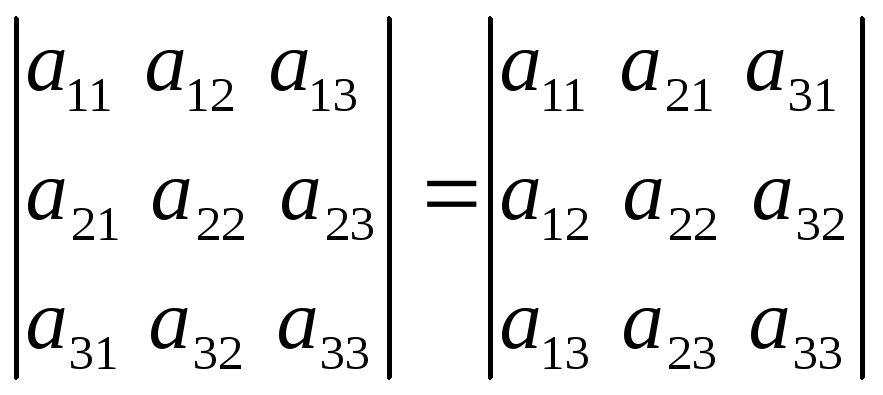   2. При перестановке двух строк или двух столбцов определитель меняет свой знак ∆ = ,

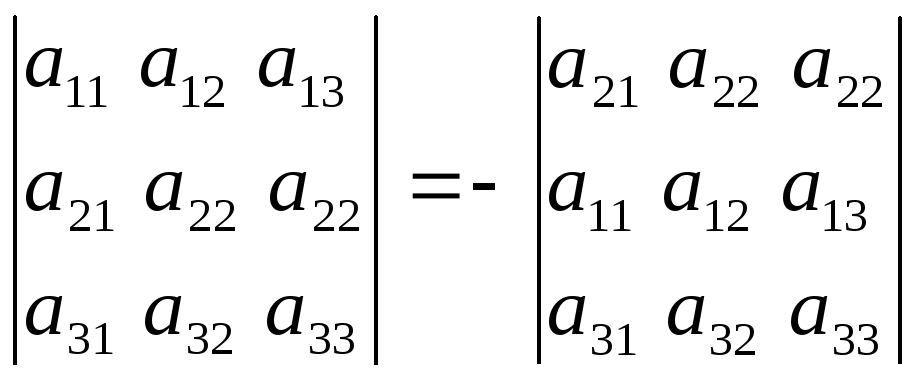Для доказательства первого и второго свойств достаточно применить правило Саррюса и сравнить полученные результаты.

3. Определитель, у которого две строки или два столбца одинаковы, равен нулю. Доказательство: Пусть определитель содержит два одинаковых столбца. Если эти столбцы поменять местами, то знак определителя должен измениться на противоположный: ∆ = -∆, 2∆ = 0,  ∆ = 0.

4. Если все элементы какого-либо столбца или строки равны нулю, то и сам определитель равен нулю.

5. Общий множитель какой-либо строки или столбца определителя можно выносить за знак определителя

Для доказательства этого свойства достаточно заметить, что определитель выражается в виде суммы, каждое слагаемое которой содержит множителем один элемент из каждой строки (столбца).

6. Если элементы какой-либо строки или столбца определителя пропорциональны элементам другой строки (столбца), то такой определитель равен нулю Это свойство является следствием свойств 3 и 5. Если вынести общий множитель одной из пропорциональных строк, то мы получим определитель, содержащий одинаковые строки. Такой определитель равен нулю.

7. Если элементы какой-либо строки или столбца определителя представляют собой суммы двух слагаемых, то определитель можно представить в виде суммы двух соответствующих определителей . Для доказательства достаточно применить правило Саррюса.

8. Величина определителя не изменится, если к элементам какой-либо строки или столбца прибавить элементы другой строки (столбца), умноженные на одно и тоже число. Следствие: Если к строке (столбцу) определителя прибавить линейную комбинацию нескольких других строк (столбцов), то значение определителя не изменится.

9. Если одна из строк (столбцов) определителя есть линейная комбинация других строк (столбцов), то определитель равен нулю. Справедливо и обратное утверждение: если определитель порядка «n» равен нулю, то одна из его строк есть линейная комбинация других строк.

10. Сумма произведений элементов какого-либо столбца или строки на алгебраические дополнения соответствующих элементов другого столбца или строки равна нулю.

Пример. Вычислить определитель:

∆ =

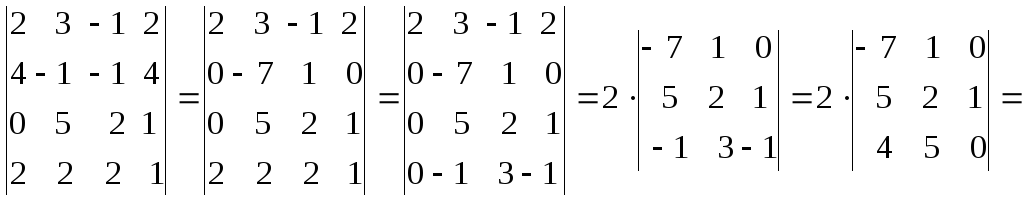
3. Решение систем линейных уравнений методом Крамера.

Рассмотрим систему из двух уравнений: 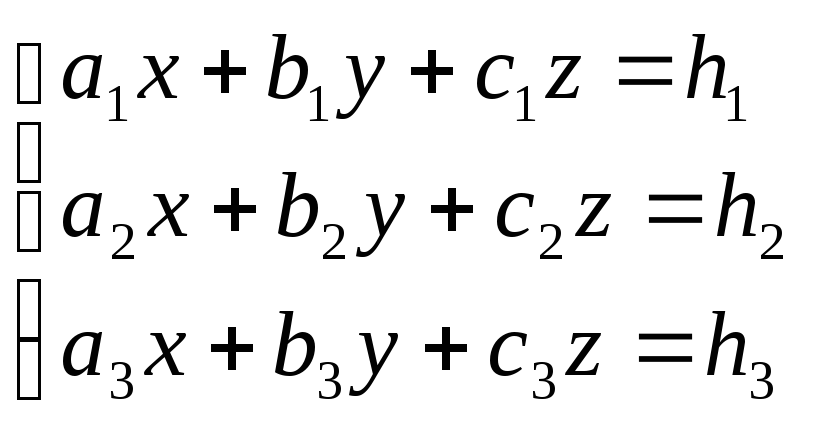(1)

с неизвестными x, y, z. Тройка чисел x_o, y_o, z_o называется решением системы, если эти числа удовлетворяют уравнениям системы.

В последующих рассуждениях основную роль будет играть определитель системы, составленный из коэффициентов при неизвестных: ∆ =.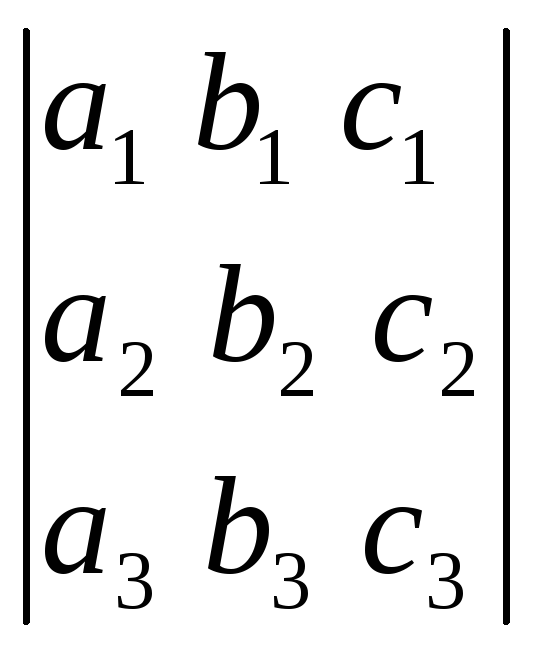

Обозначим через А₁, А₂, А₃ алгебраические дополнения элементов а₁, а₂, а₃ данного определителя. Умножим обе части первого уравнения на А₁, второго – на А₂, третьего – на А_3. Затем почтенно просуммируем эти уравнения.

. заметим, что = ∆, , (т. к. сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю).

Следовательно, ∆.

Аналогично, ∆, ∆.

Правые части полученных уравнений обозначим соответственно ∆_x, ∆_y, ∆_z. Тогда уравнения вид примут вид: , , , где

, , .

Заметим, что определители ∆_x, ∆_y, ∆_z получаются из главного определителя ∆ путём замены соответственно первого, второго и третьего столбца столбцом свободных членов.

Предположим, что . При этом условии , , .

! Если , то система (1) имеет единственное решение.

!! Если и хотя бы один из определителей ∆_x, ∆_y, ∆_z отличен от нуля, то система (1) не имеет решений, т.е. она несовместна.

!!! Если и ∆_x = 0, ∆_y = 0_, ∆_z = 0.система (1) либо не имеет решений, либо имеет бесконечно много решений. В последнем случае, по крайней мере, одно из уравнений системы будет следствием других – такая система называется неопределённой.