
20
.doc-
Отыскание исходного опорного решения транспортной задачи. Метод «северо-западного» угла. Метод минимальной стоимости.
Реш. сист. ограничений (1),(2) трансп. задачи будем записывать трансп. таблицу след. образом:
![]()
если
в каждую клетку таблицы занесены некот.
числа, то совокуп-ть этих чисел будет
реш. сист. (1),(2), если все эти числа
![]() и
сумма числе по кажд. строчке равна соотв.
запасу, а сумма чисел по кажд. столбцу
равна соотв. потребности:
и
сумма числе по кажд. строчке равна соотв.
запасу, а сумма чисел по кажд. столбцу
равна соотв. потребности:
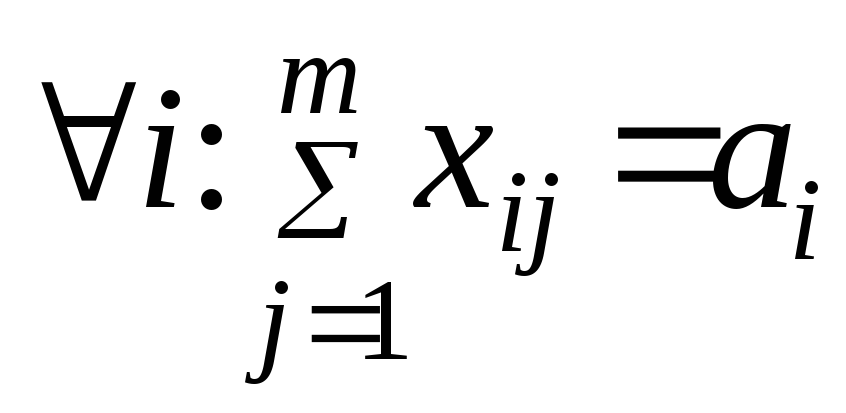 и
и
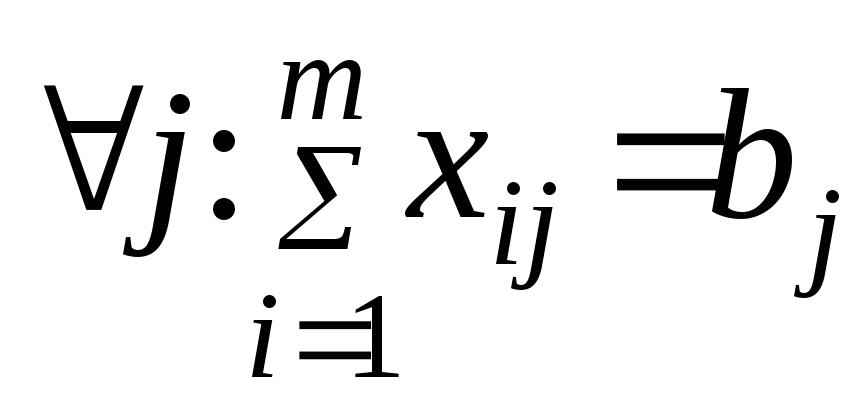
т.к. ранг сист. (1),(2) равен m+n-1, то опорное реш. должно иметь не более m+n-1 отличных от нуля переменных.
Клетки таблицы, в кот. знач. неизв. отличны от нуля, наз. занятыми.
Метод «северо-западного» угла.
|
ai/bj |
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
(1.1):
![]() =min(
=min(![]() ,
,![]() )
)
1.
![]() <
<![]() ,
,
![]() =
=![]() .
(
.
(![]() -
-![]() )
ед.
груза.
)
ед.
груза.
![]() =
min(
=
min(![]() ,
,![]() -
-![]() )
)
2.
![]() >
>![]() ,
,
![]() =
=![]() ;
;
![]() -
-![]() ;
;
![]() =
min(
=
min(![]() -
-![]() ,
,![]() )
)
|
ai/bj |
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
3.
![]() =
=![]() ,
,
![]() =
=![]()
Заполнив, двигаемся вправо по строке , если закрыт соотв. столбец, или вниз по столбцу, если закрыта соотв. строка.
И т.д. пока не будут исчерпаны все запасы и не будут удовл. все потребности.
Последняя клетка mn.
Замечание 1.
Может оказаться, что после занесения
очередной
![]() ,
закрывается одновр. i-ая
строка и k-ый столбец.
Тогда занесем в в соседнюю по строке/столбцу
клетку(в кот. меньше тариф)число ноль.
,
закрывается одновр. i-ая
строка и k-ый столбец.
Тогда занесем в в соседнюю по строке/столбцу
клетку(в кот. меньше тариф)число ноль.
Такие нули называют базисными.
Замечание 2.
Совокуп-ть чисел
![]() ,
найденных методом сев.-запад. угла –
есть система огранич., т.к. при заполн.
таблицы выполнялись рав-ва по строкам
и по столбцам, соотв. уравн-ниям сист.
(1),(2).
,
найденных методом сев.-запад. угла –
есть система огранич., т.к. при заполн.
таблицы выполнялись рав-ва по строкам
и по столбцам, соотв. уравн-ниям сист.
(1),(2).
