
22
.docx22) Метод потенциалов. Теорема о достаточном условии оптимальности опорного решения транспортной задачи.
Пусть исходное опорное решение записано в транспортной таблице, тогда в базисных клетках стоят неотрицательные числа, а свободные незаполнены (соответственно =0)
Сопоставим
каждому поставщику число
 αi
ai→αi,
а для каждого потребителя число
αi
ai→αi,
а для каждого потребителя число
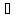 βj
v
bj→βj
и потребуем, чтобы для
каждой базисной клетки
(k,l)
выполнялось условие αi+βj=ckl
ckl
– тариф
βj
v
bj→βj
и потребуем, чтобы для
каждой базисной клетки
(k,l)
выполнялось условие αi+βj=ckl
ckl
– тариф
Получаем систему из m+n-1 уравнений и m+n неизвестных. Эта линейная система относительно неизвестных αk и βl всегда совместна. Чтобы найти какое-либо одно решение, нужно 1 неизвестное задать, а значения остальных неизвестных найти из системы. Всякое решение такой системы уравнений будем называть потенциалами данного опорного решения.
Теорема.
Пусть Х0 – опорное решение системы ограничений (1) и (2) αi i=1,m βj j=1,n – потенциалы опорного решения Х0.
Тогда, если для каждой свободной клетки транспортной таблицы выполняется условие αi + βj ≤ ckl (*), то Х0-оптимальное, следовательно, Х 0→min
Доказательство.
Доказать, Х-произвольное опорное решение (план) систем (1) и (2) , то стоимость перевозок(значение целевой функции) f(X) ≥f(X0) X0=(x011, x012,…,x0mn)
F(X)
= ≥
≥

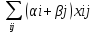 =
=
 +
+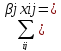
 =
=
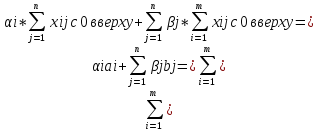
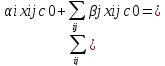
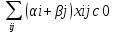 =
=
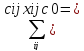 f(X0)
f(X0)
Для базисных неизвестных (αi+ βj)x0ij=cij x0ij , т к мы находим потенциалы, а для свободных клеток (αi+ βj)x0ij=cij x0ij также выполняется , т к по условию теоремы значение x0ij =0 для свободной клетки.
Если
найдется хотя бы 1 клетка, для которой
условие (*) не выполняется, то есть αi
+ βj
 ckl,
то опорное решение Х0
не является оптимальным, необходимо
перейти к новому опорному решению Х1,
на котором значение целевой функции
меньше или равно значению на опорном
решении Х0.
F(X1)
ckl,
то опорное решение Х0
не является оптимальным, необходимо
перейти к новому опорному решению Х1,
на котором значение целевой функции
меньше или равно значению на опорном
решении Х0.
F(X1)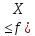 0)
0)
