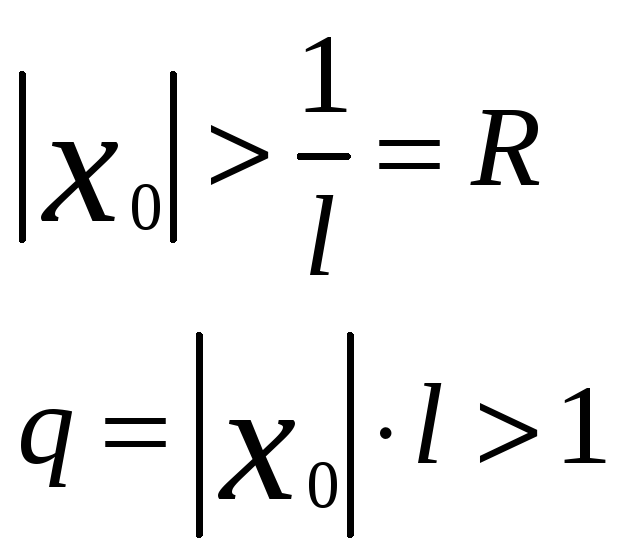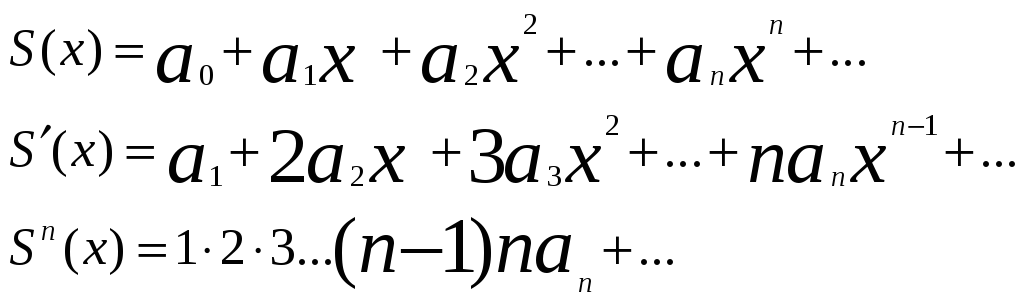25.33

25. степенным рядом называется функциональный ряд вида (1),

где , ,…, ,… - постоянные числа, называемые коэффициентами ряда.

1. интервал сходимости степенного ряда, радиус сходимости

Теорема: для каждого степенного ряда (1) существует такое число или символ R, , что ряд абсолютно сходится при каждом х, если <R; расходится, если >R

Если существует , то , при этом полагаются R=0 при , при .

Доказательство: рассмотрим ряд (1) при любом фиксированном значении . Получим числовой ряд Абсолютную сходимость этого ряда исследуем по признаку Даламбера. Если , то q=0. Ряд сходится абсолютно на всей числовой оси, , и , то . Ряд сходится при всех ; R=0

. Ряд сходится абсолютно при каждом , если

. Ряд расходится, если

Теорема устанавливает, что областью сходимости степенного ряда (1) является интервал радиуса R с цетром в начале координат, который может вырождаться в одну точку х=0 или совпадать со всей осью Ох. Число R называется радиусом сходимости степенного ряда, интервал (-R, R) называется интервалом сходимости степенного ряда. В каждой внутренней точке этого интервала ряд сходится абсолютно. Для того чтобы выяснить сходимость степенного ряда на концах интервала, т.е. при х= R и при х=- R, нужно рассмотреть степенной ряд при этих значениях х и исследовать на сходимость полученные числовые ряды.

2. Свойства степенных рядов

1) степенной ряд сходится равномерно на любом отрезке , лежащем строго внутри его интервала сходимости (-R, R) .

2) сумма степенного ряда непрерывна в каждой внутренней точке интервала сходимости.

3) степенной ряд (1) можно почленно интегрировать в интервале сходимости, т.е., если , а -сумма ряда (1), то

4) степенной ряд (1) внутри его интервала сходимости можно дифференцировать почленно, т.е. для суммы ряда существует производная и выполняется равенство

5) сумма степенного ряда = имеет производные всех порядков внутри интервала сходимости. Каждая из производных равна сумме ряда, получающегося дифференцированием ряда для предыдущей производной.

33.Потенциальное поле

Векторное поле А=P(x;y;z)i+Q(x;y;z)j+R(x;y;z)k называется потенциальным, если существует такая скалярная функция U(x;y;z), что во всех точках области V, где задано поле А, выполняется равенство gradU=A =Q , то есть равносильно утверждению dU=Pdx+Qdy+Rdz функция U(x;y;z), называется потенциалом поля А.

Теорема. Для того, чтобы векторное поле А, заданное в односвязной области V было потенциальным , необходимо и достаточно выполнение одного из след.св-в:

1) или rotA=θ

2)циркуляция поля А вдоль любого замкнутого контура Г в области V равна нулю, т.е

3) циркуляция вдоль любой кривой АВ в области V не зависит от формы кривой, а только от точек А и В.