3
.docxБилет №3. Графический метод решения задач линейного программирования.
Имеет ограниченную область применения: им можно решать задачи следующего типа:
-
Задачи в симметричной форме записи с n=2;
-
Задачи с n переменными в канонической форме, при условии что (n-r)≤2, r – ранг системы ограничений (1).
Решение задач типа1.
Найти
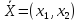 ,
который является решением системы
уравнений:
,
который является решением системы
уравнений:
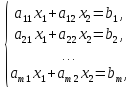 (1)
(1)
для
которой целевая функция
 (2).
(2).
Решение проходит в 2этапа:
-
Построение ОДР – область допустимых решений задачи – множество точек на плоскости
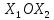 .
ОДР по условию (2) лежит в первой
координатной четверти.
.
ОДР по условию (2) лежит в первой
координатной четверти.
 m
m

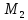



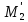
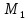


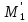



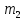


0
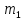
Выпишем какое-либо неравенство из системы ограничений (1):
 (4)
(4)
Выясним какое множество
 определяет это неравенство (из ОДР).
определяет это неравенство (из ОДР).
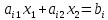 (5)
(5)
Это уравнение определяет на плоскости
прямую линию m, которая
делит плоскость
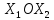 на две полуплоскости. Геометрический
смысл трёхчлена:
на две полуплоскости. Геометрический
смысл трёхчлена:
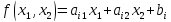
Теорема:
Для того, чтобы точки
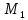 и
и
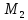 лежали по одну сторону от прямой m,
необходимо и достаточно, чтобы знак
трёхчлена
лежали по одну сторону от прямой m,
необходимо и достаточно, чтобы знак
трёхчлена
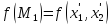 совпадал со знаком трёхчлена
совпадал со знаком трёхчлена
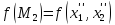 .
т.
.
т.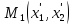 т.
т.
Доказательство:
Проведём прямые: через т. –
–
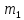 и через т.
и через т.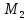 –
–
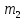 ,
причём
,
причём
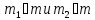 ,
,
 и
и
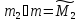 .
т.
.
т. и т.
и т.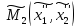 .
.
Рассмотрим векторы:

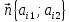 .
.
Вектор
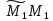 и
и
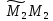 коллинеарны
коллинеарны

 существуют числа
существуют числа
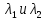 ,
такие что:
,
такие что:
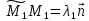 (6) и
(6) и
 (7).
(7).
То есть т.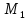 и т.
и т.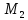 лежат по одну сторону от прямой m,
тогда и только тогда, когда
лежат по одну сторону от прямой m,
тогда и только тогда, когда
 , то есть знаки
, то есть знаки
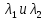 совпадают.
совпадают.
Подсчитаем значение трёхчлена в т. :
:
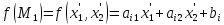
Ищем
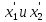 из равенств (6) и (7):
из равенств (6) и (7):
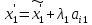
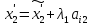 (8)
(8)

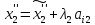

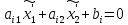 так как
так как
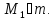
Точно также мы можем получить:
 .
.
Знак трёхчлена
 совпадает со знаком
совпадает со знаком
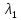 ,
а знак трёхчлена
,
а знак трёхчлена
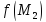 -
-
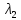
 совпадение знаков этих трёхчленов
равносильно тому, что т.
совпадение знаков этих трёхчленов
равносильно тому, что т. лежат по одну сторону от прямой m.
лежат по одну сторону от прямой m.
Следствие:
Для точек одной из полуплоскостей (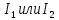 )
выполняется неравенство:
)
выполняется неравенство:
 (10), а для точек других полуплоскостей:
(10), а для точек других полуплоскостей:
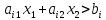 .
.
Поэтому для определения по какую сторону ограничивающей прямой m располагается полуплоскость, соответствующая заданному неравенству, достаточно в неравенство подставить координаты какой-либо одной точки, не лежащей на прямой m. Если эта точка будет решением неравенства
 , то и все точки этой полуплоскости будут
решениями этого неравенства. То есть
областью решений неравенства (10) будет
полуплоскость, содержащая выбранную
точку. Если выбранная точка не является
решением неравенства (10), то областью
решения неравенства (10) будет другая
полуплоскость, не содержащая выбранную
точку.
, то и все точки этой полуплоскости будут
решениями этого неравенства. То есть
областью решений неравенства (10) будет
полуплоскость, содержащая выбранную
точку. Если выбранная точка не является
решением неравенства (10), то областью
решения неравенства (10) будет другая
полуплоскость, не содержащая выбранную
точку.
-
Нахождение в ОДР оптимального решения.
Рассмотрим уравнение
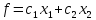 (3).
(3).
При конкретном значении
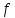 ,
это уравнение определяет на плоскости
,
это уравнение определяет на плоскости
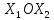 прямую линию. При изменении числа
прямую линию. При изменении числа
 ,
мы получим семейство параллельных
прямых (прямые
,
мы получим семейство параллельных
прямых (прямые
 ,
так как имеют одинаковый угловой
коэффициент
,
так как имеют одинаковый угловой
коэффициент
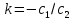 ).
).
Каждая из этих прямых называется линией
уровня, так как согласно (3) на каждой их
этих прямых значение
 постоянно.
постоянно.
Найдём градиент функции (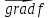 ):
):
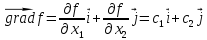
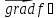 линии
уровня и показывает направление, по
которому нужно перемещать линии уровня,
чтобы значение
линии
уровня и показывает направление, по
которому нужно перемещать линии уровня,
чтобы значение
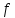 возрастало.
возрастало.
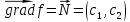 – обозначаем для удобства.
– обозначаем для удобства.
Определение:
Линия уровня, имеющая общие точки с ОДР
и расположенная так, что ОДР делит
координатную плоскость
 ,
называется опорной прямой.
,
называется опорной прямой.
Чтобы найти оптимальное решение выполним следующее:
-
Строим вектор
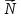 в начале координат.
в начале координат. -
Перпендикулярно вектору
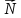 проведём одну из линий уровня, имеющую
общие точки с ОДР.
проведём одну из линий уровня, имеющую
общие точки с ОДР. -
Перемещая эту линию уровня в направлении вектора
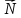 в задаче на max, или в
противоположном направлении в задаче
на min, найдём опорную
прямую.
в задаче на max, или в
противоположном направлении в задаче
на min, найдём опорную
прямую. -
Совместно решив уравнение прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой, найдём оптимальное решение.
В зависимости от вида ОДР и целевой
функции
 задача может иметь: единственное решение,
бесконечное множество решений или не
иметь решений ввиду несовместимости
ограничений или неограниченности
целевой функции в ОДР.
задача может иметь: единственное решение,
бесконечное множество решений или не
иметь решений ввиду несовместимости
ограничений или неограниченности
целевой функции в ОДР.
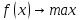 единственное решение т.
единственное решение т.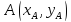 :
:
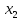



ОДР





опорная прямая









линия уровня
Бесконечное множество решений (так как пересекаются по прямой):









опорная прямая
ОДР






0
Решений нет ввиду неограниченности целевой функции:






ОДР



0