Lektsii / 22 Воздействие струи на преграды

Воздействие струи на преграду 22-3

Активное воздействие струи на неподвижную и подвижную преграду

Потоки жидкости или газа, не имеющие твердых границ, называются ждкими или газовыми струями.

Классификация: затопленные (вода в воде), незатопленные (вода в воздухе); свободные и ограниченные (пристеночные); по форме осесимметричные (круглое сечение) и плоские.

В структуре незатопленной струи 3 части.

1. компактная часть (сплошной цилиндр)

2. раздробленная часть (крупные части)

3. распыленная часть (отдельные капли)

Силы, действующие на струю: тяжести, сопротивления среды, инерционные силы от вихрей турбулентности, поверхностного натяжения.

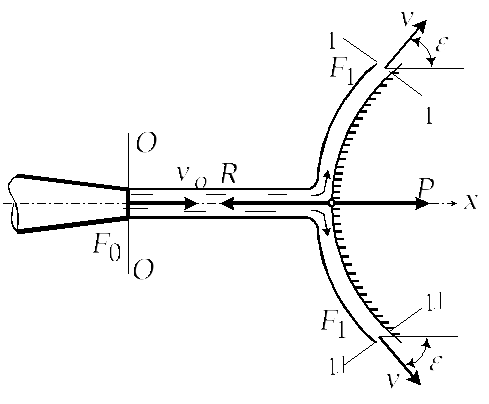
Воздействие струи на неподвижную преграду

Из сопла площадью сечения со скоростью вылетает струя жидкости и ударяется о криволинейную преграду. Струя разбивается на две части, обрекает преграду и со скоростью под углом к горизонту покидает преграду. Сила действия струи на преграду , сила воздействия преграды на струю . Очевидно .

Применим к жидкости, заключенной между сечениями 0-0 и 1-1 (1’-1’) теорему об изменении количества движения в проекции на ось . Изменение количества движения равно импульсу силы.

, где – промежуток времени, – масса жидкости, проходящая через сечение за это время. Трением и весом пренебрегаем, тогда по закону сохранения энергии . Учитываем, что массовый расход и

. Получим

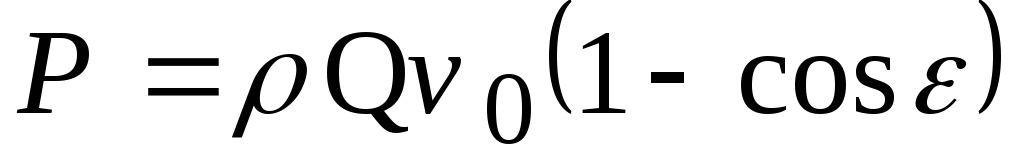
Сила воздействия струи на преграду

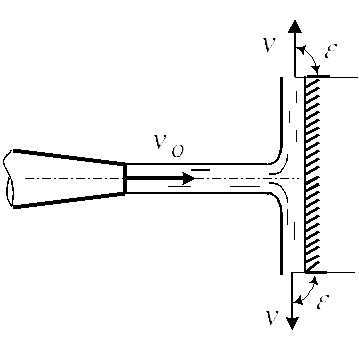
	Если преграда плоская, то , .
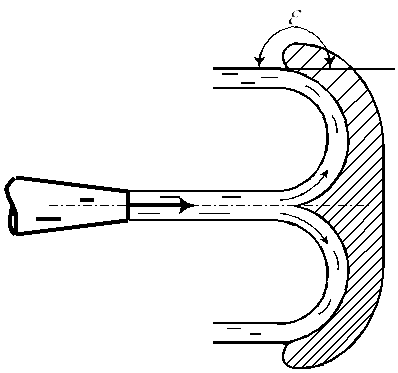
	Если выполнить преграду в виде ковша, то происходит полный разворот потока ,

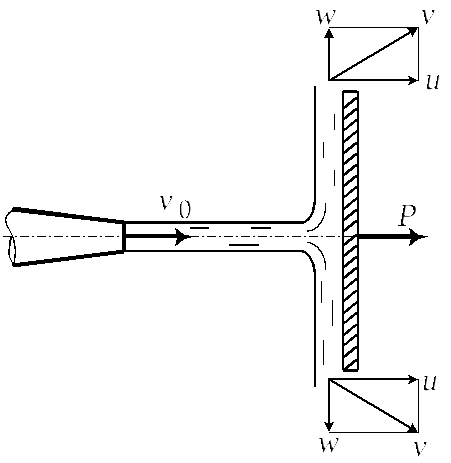
Воздействие струи на подвижную преграду

Рассмотрим воздействие струи на систему плоских пластинок (турбинное колесо) Сила такого воздействия . Скорость схода жидкости с пластинки (абсолютная скорость), может быть представлена как сумма скорости самой пластинки (переносная скорость) и скорости движения жидкости по пластинке (относительная скорость), т. е. По условию сохранения кинетической энергии струи , это скорость, с которой струя ударяется в пластинку.

Сила воздействия струи на пластинку .

Мощность, которая передается пластинчатому колесу, .

При постоянной плотности , расходе и скорости струи на выходе из сопла мощность зависит только от скорости движения пластинки , т.е. , причем зависимость квадратичная (парабола). Ее корни:

При имеем , однако /

При сила воздействия , и, следовательно, .

Для нахождения значения при котором величина максимальна можно воспользоваться тем, что в точке максимума первая производная функции равна нулю. Раскроем скобки

. , откуда .

Тот же вывод может быть получен без взятия производной, если вспомнить, что парабола имеет максимум посередине между корнями.

Максимальная мощность ( теоретически, в действительности меньше из-за потерь, ).

Кинетическая энергия струи на выходе из сопла

Следовательно в случае плоской пластинки используется только половина располагаемой энергии струи, оставшаяся половина покидает лопатки со выходной скоростью . Чтобы практически полностью использовать энергия струи следует выполнить лопатки в форме ковша с полным разворотом потока.

Рассмотрим истечение струи из резервуара через отверстие. Скорость струи (без учета потерь) определяется по формуле Торричелли , где – действующий напор. Если на пути струи расположить плоскую преграду, то на нее будет действовать сила , где . Окончательно . К слову заметим, что в этом случае на резервуар действует рвная по величине и противоположная по направлению сила.

Если отверстие перекрыть неподвижной преградой, то на нее будет действовать сила гидростатического давления, равная произведению давления жидкости в резервуаре на глубине на площадь . Интересно, что величина этой силы в два раза меньше, чем сила действия струи.