Кольцевые и тупиковые водопроводные сети

Водопроводные сети, по которым вода из водонапорной башни поступает к потребителям, делят на разветвленные (тупиковые) и кольцевые.

	Разветвленные трубопроводы состоят из основной магистрали и отходящих от узлов сети ответвлений, которые могут состоять из одной линии (простые ответвления) или нескольких участков трубопроводов (сложные ответвления).
	Городские водопроводы обычно выполняются в виде кольцевых сетей обеспечиваются водой от двух и более водонапорных башен Б. В узлах 1-9 находятся потребители (например жилые массивы, предприятия и т.п.)

Кольцевая сеть позволяет осуществлять водоснабжение всех потребителей в случае аварии или ремонта отдельных участков водопроводной сети. При этом, конечно, потребности в воде будут удовлетворяться не полностью, а , например, на несколько часов в сутки, причем иногда обеспечиваются лишь нижние этажи зданий и т.п., но все же водоснабжение не буден отключено полностью на все время ремонта, что может произойти, если сеть тупиковая.

Строительными нормами и правилами рекомендуется обеспечить пьезометрический напор не менее 10 м при одноэтажной застройке, добавляя 4 м на каждый этаж.

Расчет разветвленного трубопровода.

Определить расход жидкости, протекающей по разветвленному трубопроводу в пункты 1 и 2 (истечение в атмосферу). Напор в резервуаре постоянен и известен. Длины и диаметры отдельных участков трубопровода известны. Кинематическая вязкость жидкости и абсолютная эквивалентная шероховатость известны. Местными потерями напора и скоростным напором пренебречь.

Примечание.

1. Как правило задается не кинематическая вязкость, а вид жидкости и рабочая температура. Кинематическую вязкость берут по таблицам в справочниках.

2. При истечении в атмосферу не потерь на вход в бак, однако в точных расчетах необходимо учитывать скоростной напор выходящей из трубы жидкости. Если им пренебречь и не учитывать местные потери, то весь располагаемый напор равен сумме потерь напора по длине в общем трубопроводе и в разветвленной части (в двух трубопроводах разветвления напор одинаков, однако длины и/или диаметры различны, а значит различны средние скорости и расходы).

Решение.

В разветвленном трубопроводе сохраняется баланс расходов .

Неизвестны два расхода, третий находится по балансу. Потери в ветвях разветвляющейся части одинаковы, т.е. . Располагаемый напор. Потери в каждом трубопроводе рассчитываются по формуле Дарси-Вейсбаха.

Расход по участку . Площадиизвестны. Тогда.

В первом приближении примем, что режим движения жидкости в трубопроводе турбулентный, квадратичная область сопротивления (в дальнейшем это утверждение будет уточнено). Коэффициент Дарси для каждого диаметра может быть определен по формуле Шифринсона . Потери в каждом участке трубопровода могут найдены через его расходную характеристику, при чем последняя не берется из таблиц, а определяется аналитически.. Здесь расходная характеристика.

Получим шесть уравнений с шестью неизвестными (расходы и потери напора в участках)

,,,,,.

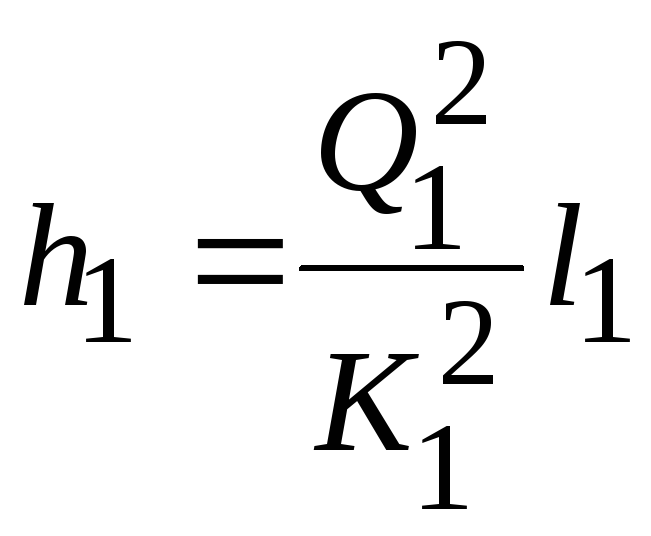Несложные алгебраические преобразования приводят к следующим результатам:

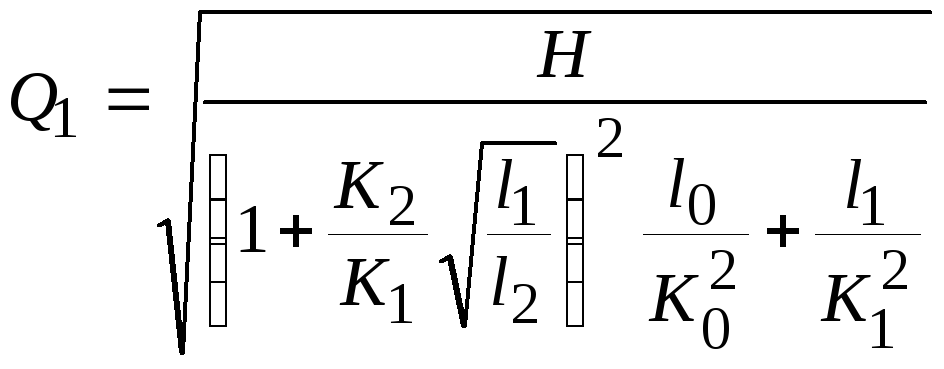
Уточнение полученных результатов производится в следующей последовательности. Находят средние скорости во всех участках трубопровода, числа Re. Определяют область гидравлического сопротивления, в которой работает каждый участок, и по соответствующим эмпирическим формулам (Блазиуса, Альтшуля, Шифринсона и др.) вычисляют значение коэффициента Дарси. Уточняют значения расходных характеристик участков и вновь вычисляют расходы по участкам.

Такой способ позволяет получить решение с любой требуемой точностью.

Графоаналитический способ решения задачи.

Задаются начальным приближением по скорости. Пусть, например 2 м/с по участку 1.

Скорость по участку 2 определяют из простой пропорции (равенство потерь по длине при одинаковом коэффициенте Дарси.

.

Находим расход по участкам и общий расход а также скорость на участке 0.

На каждом участке находим число Re, определяем область сопротивления и по соответствующей формуле находим коэффициент Дарси. Вычисляем потери по длине на каждом участке.

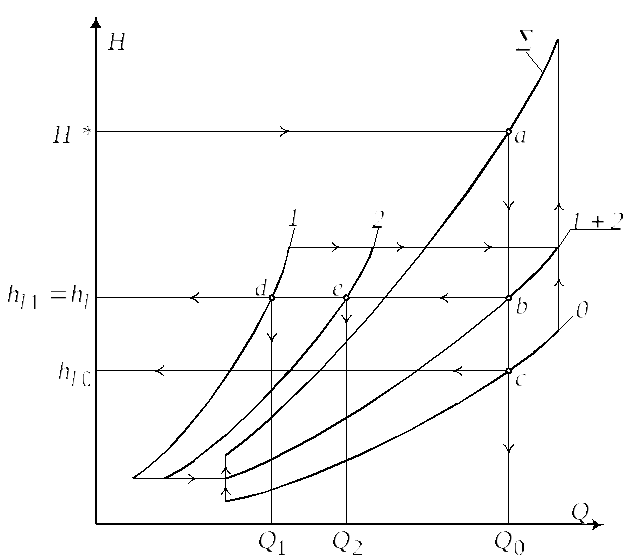
На одном графике строим расходные характеристики участков 1 и 2. Эти участки соединены параллельно, суммарная характеристика строится путем суммирования расходов при одинаковом напоре (кривая 1+2). На этом же графике строим характеристику участка 0. Этот участок соединен с участком 1+2 последовательно, суммарная характеристика всего трубопровода строится суммированием напоров при одинаковом расходе (кривая ). По заданному суммарному напорупо кривойнаходим расход через весь трубопровод и через участок 0. (Линия-a-b-c-.) Точкеbсоответствует напор на участках 1 и 2, точкеснапор на участке 0. Пересечение горизонтали через точкуb с характеристиками трубопроводов 1 и 2 определяет расходы в них. (Линииb-d-и b-e-.)

Рассмотренный графоаналитический способ расчета не дает точного решения, однако позволяет разработать алгоритм его нахождения с использованием средств вычислительной техники.

1Напомним использованные сведения из математики.

Квадрат суммы . Квадрат разности.

Постоянные выносятся за знак интеграла. Интеграл суммы (разности) есть сумма (разность) интегралов.

Табличные интегралы