Теорема Гаусса в дифференциальной форме

Теорема Гаусса в интегральной форме

С помощью теоремы Гаусса в интегральной форме нельзя определить, как связан исток линий вектора электрического смещения в данной точке поля с плотностью свободных зарядов в этой же точке. Чтобы узнать это, рассмотрим дифференциальную форму теоремы Гаусса. Для этого разделим обе части уравнения интегральной формы записи теоремы Гаусса на одну и туже скалярную величину V (объем), находящийся внутри замкнутой поверхности:

.

Это выражение справедливо для V любой величины, устремим V к 0.

Предел отношения потока вектора электрического смещения сквозь замкнутую поверхность, ограничивающую некоторый объем, к объему называют дивергенцией вектора электрического смещения.

Или вместо слова «дивергенция» употребляют термины «расхождение».

,

где – объемная плотность заряда:

.

1. Если объемная плотность зарядов >0 в данной точке поля положительна, то из бесконечно малого объема окружающего данную точку поля, линии вектора электрического смещения исходят (исток).

2. Если объемная плотность зарядов <0 в данной точке поля отрицательна, то в бесконечно малый объем окружающий данную точку поля, линии вектора электрического смещения входят (сток).

3. Если объемная плотность зарядов =0 в данной точке поля равна нулю, то в данной точке поля нет ни стока, ни истока. Линии вектора электрического смещения 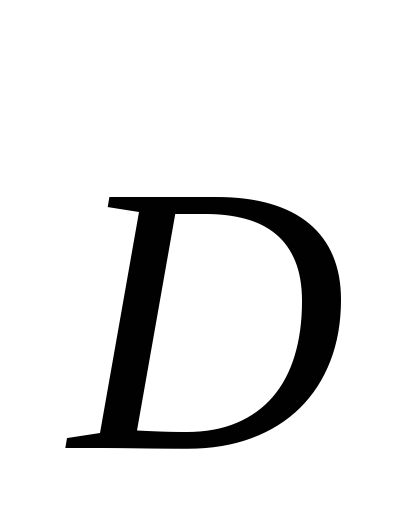проходят через данную точку пространства.

Силовые линии начинаются и заканчиваются на зарядах.

Теорема Гаусса в дифференциальной форме

Если среда однородна и изотропна, то ее и тогда:

.

Разложим дивергенцию в декартовой системе координат:

;

;

.

Ёмкость

Если два проводящих тела разделены диэлектриком и несут на себе равные по значению и противоположные по знаку заряды, то в пространстве между ними создается электрическое поле.

Под емкостью С между двумя телами, на которых имеются равные и противоположные по знаку заряды, понимают абсолютную величину отношения заряда на одном из тел к разности потенциалов между телами.

.

Емкость измеряется в Фарадах .

Емкостью обладают любые два тела, разделенные диэлектриком.

Техническое устройство определенной емкости – это конденсатор.

Емкость линейного конденсатора не зависит от заряда и разности потенциалов, а зависит от геометрических размеров конденсатора и свойств диэлектрика находящегося между пластинами.

Методика расчёта ёмкости тела правильной формы:

Условно считают заряд известным, через него выражают напряжение и подставляют в формулу для емкости, где заряд сокращают.

Емкость плоского конденсатора

Применим теорему Гаусса в интегральной форме:

.

Поле плоского конденсатора равномерно, поэтому можно убрать знак интеграла:

.

Заряд равномерно распределен по поверхности пластин, поэтому в расчетах удобно пользоваться понятием поверхностной плотности заряда.

;

;

.

Зная напряженность электростатического поля найдем напряжение:

.

Тогда

.

Ёмкость цилиндрического конденсатора

(коаксиального кабеля)

Напряженность поля цилиндрического конденсатора (см. применение теоремы Гаусса):

.

Зная напряженность электростатического поля найдем напряжение:

.

Заряд распределен по длине.

,

где l – длина кабеля.

Тогда емкость цилиндрического конденсатора:

.

Ёмкость двух проводной линии

Если d >> R_{n ,} то .

Если d ≈ R_{n ,} то .

Ёмкость сферического конденсатора

.

Если R₂ устремить к бесконечности, то получим формулу для шара:

.

Ёмкость двухслойного цилиндрического конденсатора

Поверхность каждого слоя эквипотенциальна, поэтому её можно заменить металлической поверхностью, сообщив некоторый потенциал (второе следствие теоремы единственности решения). Получим два конденсатора один внутри другого.

+

Конденсаторы соединим последовательно:

;

;;

;.