Уравнение электромагнитного поля в комплексной форме

Если напряженность электрического и магнитного поля изменяется по синусоидальному закону, то мы можем записать.

- комплексная амплитуда

- комплексная амплитуда

Im – мнимая часть

Индекс м опускаем, так как мы имеем дело с действительными значениями.

Первое уравнение Максвелла в комплексной форме

- первое уравнение Максвелла в комплексной форме.

Второе уравнение Максвелла в комплексной форме

- второе уравнение Максвелла в комплексной форме.

Теорема Умова-Пойтинга в комплексной форме

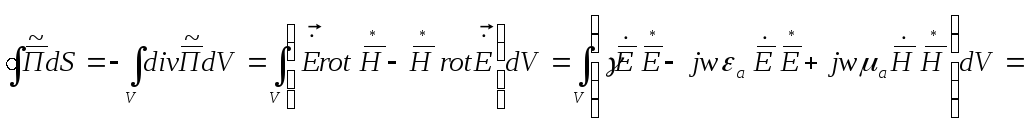
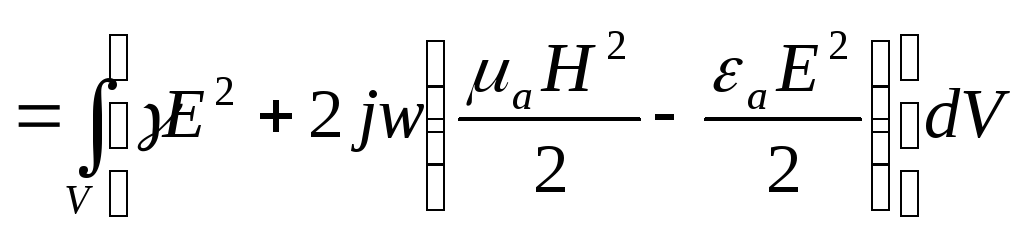
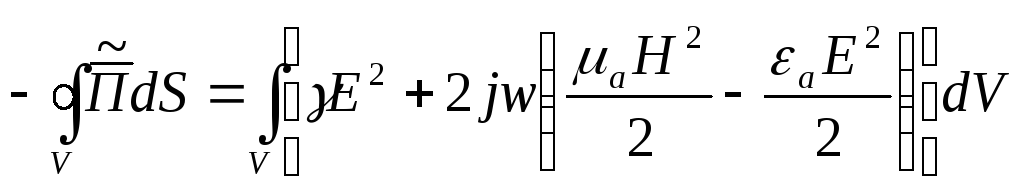
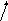
P Q

- теорема Умова-Пойтинга в комплексной форме.

Электромагнитные волны

Напряженность электрического поля и магнитногоизменяются по гармоническому закону, то есть представляют собой волны. Обратимся к первому и второму уравнениям Максвелла.

Даже при очень больших частотах удельная проводимость будет , поэтому.

Решим первое и второе уравнение совместно, для этого возьмём от первого уравнения.

/

- уравнение электромагнитной волны для .

Для того чтобы найти , необходимо решить данное уравнениеотносительно, а результат подставить в первое уравнение Максвелла.

Плоская электромагнитная волна

Под плоской электромагнитной волной понимают волну вектора напряженности электрического поля и магнитного поля, которые расположены в плоскости перпендикулярно направлению распространения волны и изменяются только в функции координатыzи времениt.

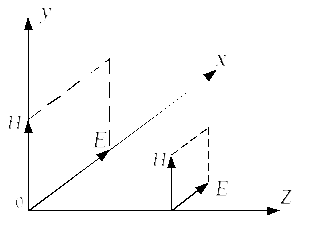
В дальнейшем под плоской электромагнитной волной будем понимать плоскую линейно - поляризованную волну, вектор напряженности электрического поля которой направлен по оси Х, а вектор напряженности магнитного поля по Y.

Совместим мнимую ось с осью Y, получим, что:

Решим уравнение для плоской электромагнитной волны.

- дифференциальное уравнение второго рода.

Решение дифференциального уравнения второго рода в общем виде

,- постоянные интегрирования определяются из граничных условий.

- постоянная распространения электромагнитной волны.

Найдем постоянную распространения из характеристического уравнения

, где

- коэффициент затухания

- коэффициент фазы

Найдем напряженность электрического поля из первого уравнения Максвелла

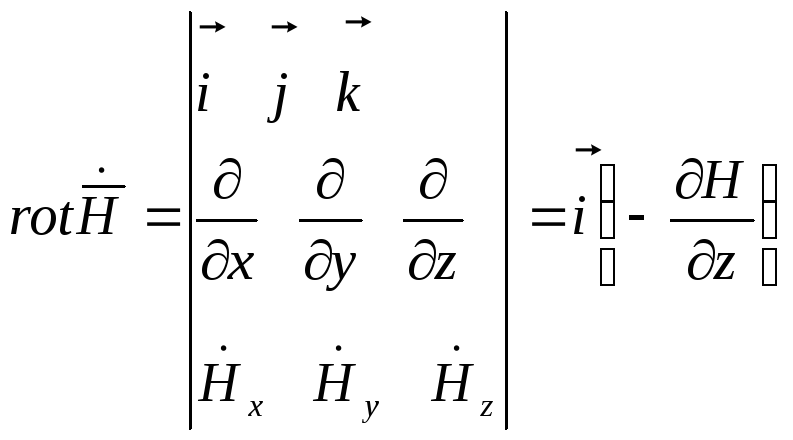
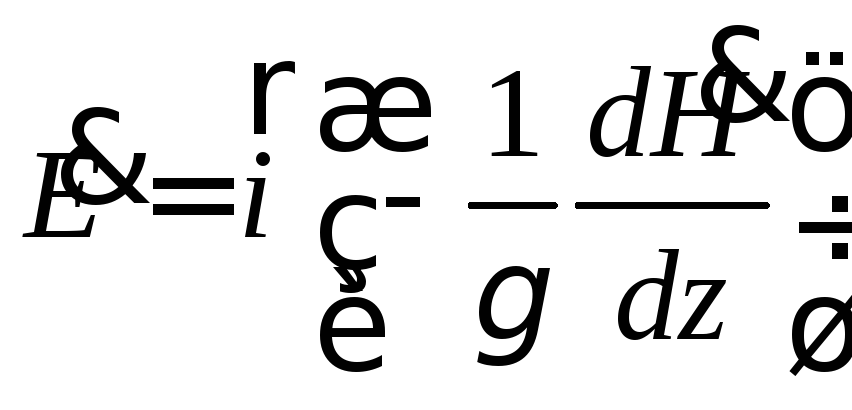
Единичный орт iговорит о том, что вектор напряжённости электрического поля направлен вдоль оси Х.

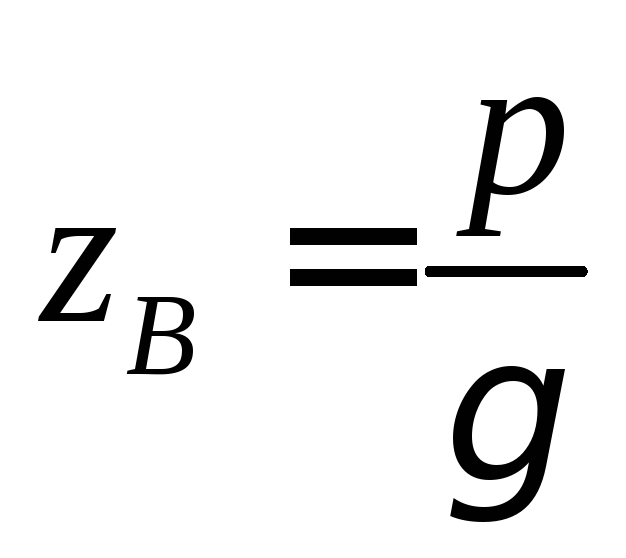- волновое сопротивление.

[Ом] зависит от свойств среды и угловой частоты

Проекция вектора напряженности электрического поля на ось «х» равна:

Проекция вектора напряженности магнитного поля на ось «у» равна:

Найдем направление вектора Пойнтинга

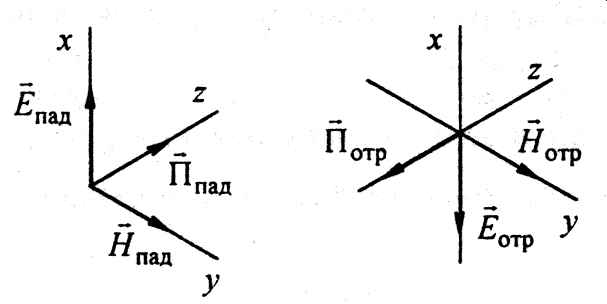
Из рисунка видно, что движение энергии падающей волны происходит вдоль положительного направления оси z, а отражённой - вдоль отрицательного направления направления осиZ.

Тогда соотношение

имеет аргумент, поэтому для одной и той же точки пространства сдвиг во времени междуибудет равен.

Плоская электромагнитная волна в однородном проводящем полупространстве

Рассмотрим вопрос о распространении плоской электромагнитной волны в однородной проводящей среде, простирающейся теоретически в бесконечность.

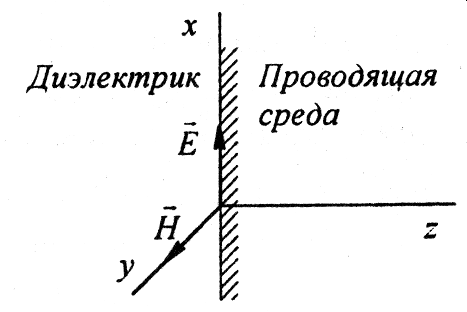
Электромагнитная волна проникает из диэлектрика в проводящую среду и распространяется в последней. Так как среда простирается теоретически в бесконечность и падающая волна в толще проводящей среды не встречает границы, которая «возмутила» бы ее распространение, то отраженной волны в данном случае не возникает.

При наличии только одной падающей волны

и

Постоянную интегрирования С₂, найдем из граничных условий. Если обозначить

напряженность магнитного поля на поверхности проводящей среды через ,то при z = 0

Поэтому с учетом того, что p=k(1+j) получаем

В свою очередь

.

Чтобы записать выражения для мгновенных значений Н и Е, необходимо правые части данных уравнений умножить на и взятьмнимые части от получившихся произведений.

Получим:

и

Проанализируем полученные выражения. Амплитуда Н равна . Амплитуда Е равна. По мере увеличения Z множитель уменьшается по показательному закону. Следовательно, по мере проникновения электромагнитной волны в проводящую среду амплитуды Е и Н уменьшаются по показательному закону.

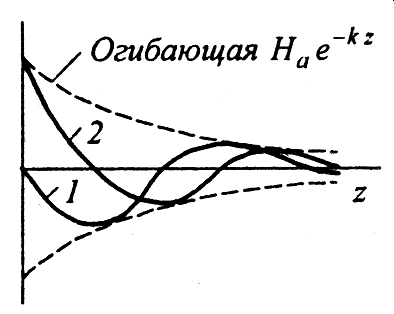
Если принять , то на графике мгновенных значений Н в функции отz будет получена кривая 1 при и кривая2 при .

Для того чтобы охарактеризовать, насколько быстро уменьшается амплитуда падающей волны по мере проникновения волны в проводящую среду, вводят понятие глубины проникновения.

Под глубиной проникновения понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором амплитуда падающей волны Е (или Н) уменьшается раз. Глубину проникновения определяют с помощью выражения

Отсюда следует, что или

Глубина проникновения зависит от свойств проводящей среды (и) и частоты. Так, если электромагнитная волна имеет частотуи проникает в проводящую среду, у которой и , то

Глубина проникновения , т.е. на расстоянии в 0,007 см амплитуды Н и Е снизились в 2,7183 раза.

Под длиной волны в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z) на котором фаза колебания изменяется на . Длину волны определяют из уравнения, отсюда

Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу. Фаза колебания определяется выражением . Производная от постоянной величины есть нуль, поэтому

или ;;

Эффект быстрого затухания широко используются на практике:

Электромагнитные экраны, нагрев металлических деталей перед ковкой, сушка древесины, наплавка и реставрация инструмента, поверхностная закалка стальных инструментов и деталей, нагрев несовершенных диэлектриков.

Экранирование в переменном электромагнитном поле.

Основано на том, что электромагнитная волна протекая в стенки экрана, быстро затухает, расходуя энергию на покрытие потерь обусловленными вихревыми токами в стенках экрана. Если экран выполнен из ферромагнитного материала, то экранирование достигается за счёт стремления силовых линий пойти по участкам с меньшим магнитным сопротивлением.