Полная система уравнения электромагнитного поля

Электромагнитное поле определяется четырьмя векторами:

Вектора напряженностей электрического и магнитного поля находят из первого и второго уравнения Максвелла:

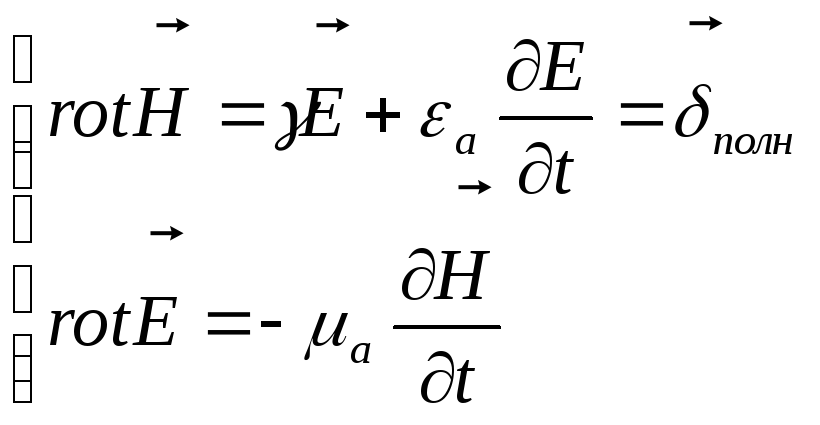
Для однозначного определения вектора по заданному ротору, задаемся дивергенцией:

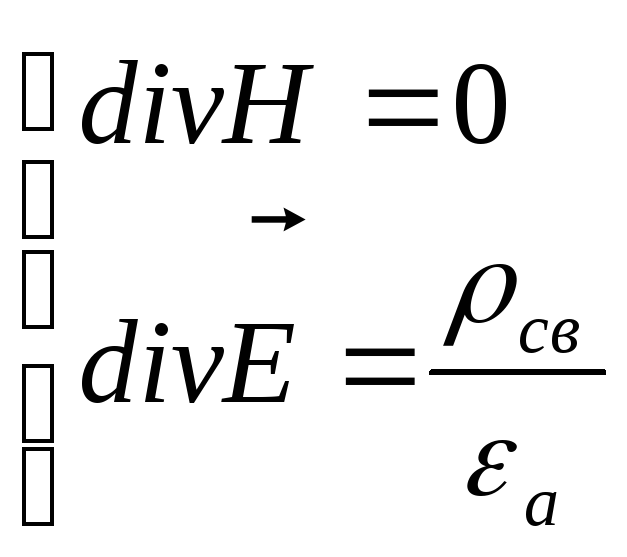
Тогда полная система уравнений:

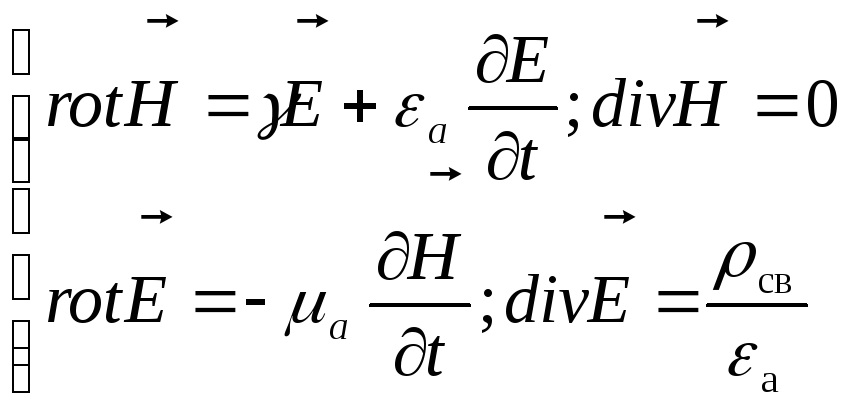
При решении задач должны быть учтены граничные условия:

Эту систему уравнений дополняют уравнением непрерывности линий плотности полного тока и уравнением Умова-Пойтинга.

Физический смысл основных уравнений переменного электромагнитного поля заключается в том, что магнитное поле всегда вихревое, возбуждается оно как движущимися зарядами, так и изменяющимся во времени электрическим полем. Электрическое поле может быть вихревым, в этом случае оно возбуждается изменяющимся во времени магнитным полем, и безвихревым, если оно возбуждается постоянными во времени электрическими зарядами.

Электрическое и магнитное поля взаимосвязаны и представляют собой проявления единого электромагнитного поля, которое находится в движении и несёт с собой запас энергии.

Теорема Умова-Пойтинга

Теорема Умова-Пойтинга выражает закон сохранения энергии. Она связывает изменение энергии в некотором объёме с потоком энергии через поверхность, ограничивающую этот объём.

1) -первое уравнение Максвелла

2) - второе уравнение Максвелла

Для того, чтобы получить выражение, в которое бы вошла полная энергия в каком-то объёме dV, необходимо умножить первое уравнение Максвелла на , а второе уравнение Максвелла на.

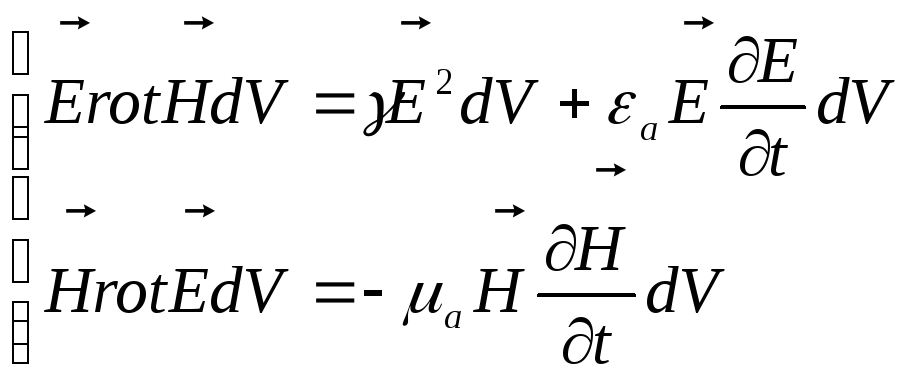
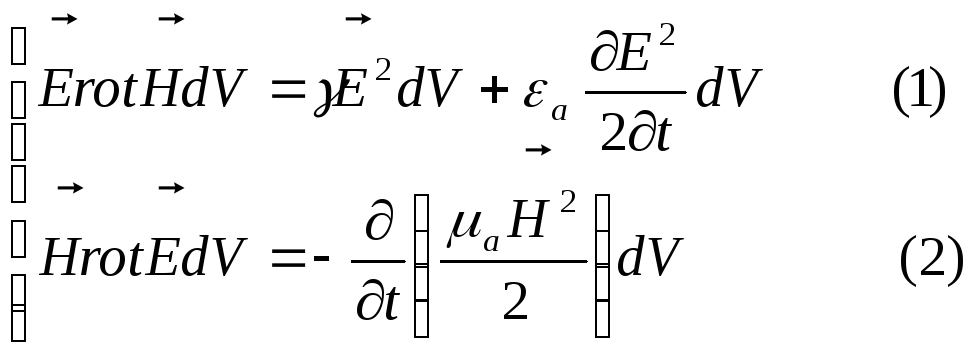
Вычтем из уравнения (1) уравнение (2).

видно, что левая часть есть дивергенция со знаком «-»

Для сокращения векторное произведение наобозначим через

- вектор Пойтинга

Таким образом, вектор Пойтинга имеет размерность мощности (или энергии в единицу времени), отнесенной к единице поверхности и направление его совпадает с направлением движения острия правоходного винта, если головку последнего вращать по кратчайшему расстоянию от к.

Рассмотрим некоторый конечный объем

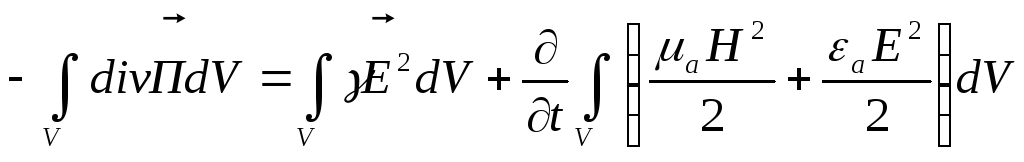
Заменим объемный интеграл на поверхностный на основании теоремы Остроградского - Гаусса

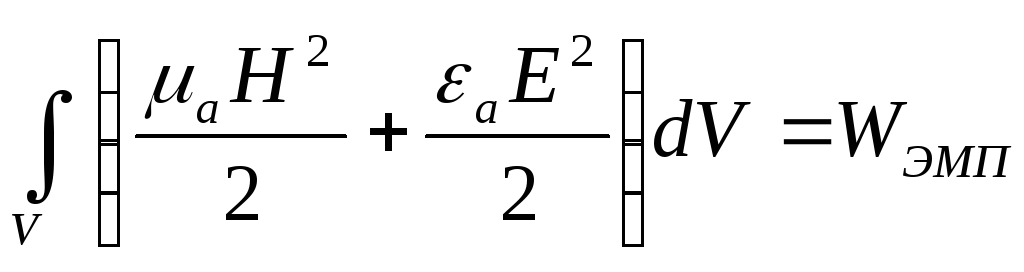- запас электромагнитной энергии.

- теорема Умова-Пойтинга

- мощность тепловых потерь - энергия, выделяющаяся в виде теплоты в единицу времени в единице объема.

- скорость изменения запаса электромагнитной энергии.

- поток вектора Пойтинга, входящий в поверхность S или мощность, передаваемая внутрь поверхности. Размерность ВА.

Так как вектор направлен внутрь объема, а нормаль направлена перпендикулярно наружу, то угол между нормалью и вектором будет больше 90⁰, поэтому скалярное произведение вектора Пойтинга на нормаль всегда будет иметь отрицательное значение, следовательно, знак «-» в левой части уравнения делает эту часть положительной.

Вывод:

Теорему Умова-Пойнтинга трактуют, как уравнение энергетического баланса: левая часть - это мощность, доставляемая в виде вектора Пойтинга внутрь некоторого объема; правая часть - это энергия, расходуемая и запасаемая в единице времени в единице объема.

Пример.

Энергия постоянного тока передается по коаксиальному кабелю. Между жилой и оболочкой пространство заполнено идеальным диэлектриком. R₁ – радиус жилы, R₂ – радиус оболочки. Проводимость материала жилы равна бесконечности , т.е. потерь нет.

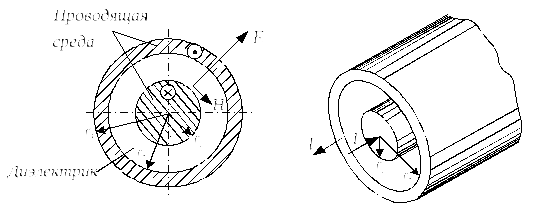
R₁ < R < R₂

Вектор Пойтинга направлен от нас (от источника у нагрузке). Так как , то:

Из закона полного тока

Вектор напряжённости в диэлектрике при постоянном токе определяется также, как и в условиях электростатики

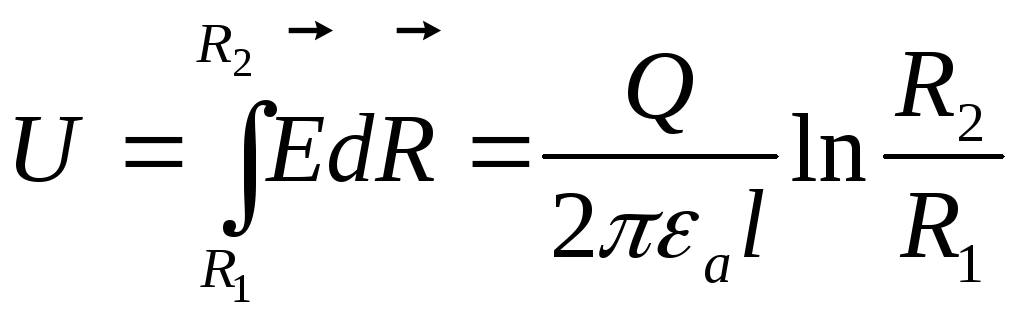–напряжение между жилой и оболочкой

–полный заряд жилы на длине l

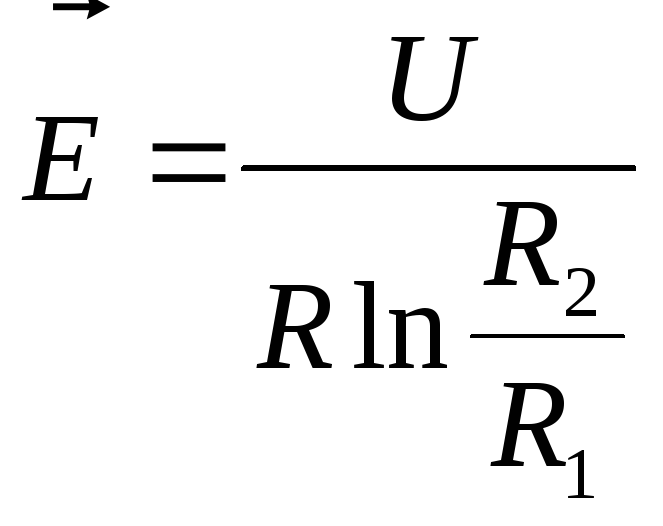
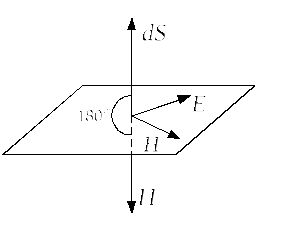
Вектор Пойнтинга в некоторой точке диэлектрика

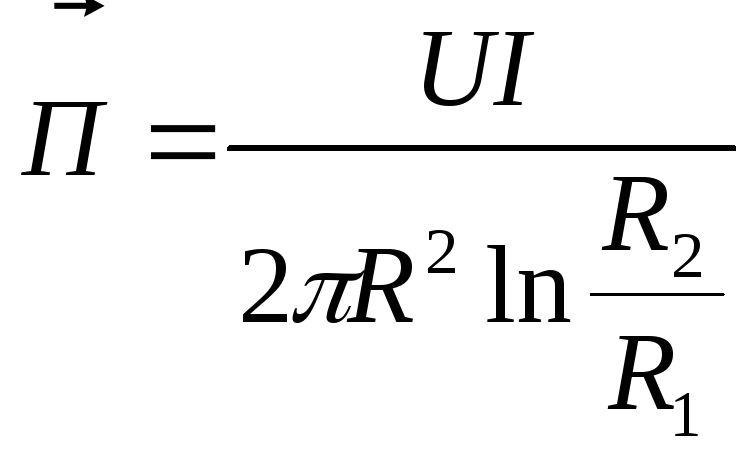
Поток вектора Пойнтинга

Так как вектор Пойнтинга и нормальрасположены под углом 180 градусов, то избавляемся от скалярного произведения и знака «-»

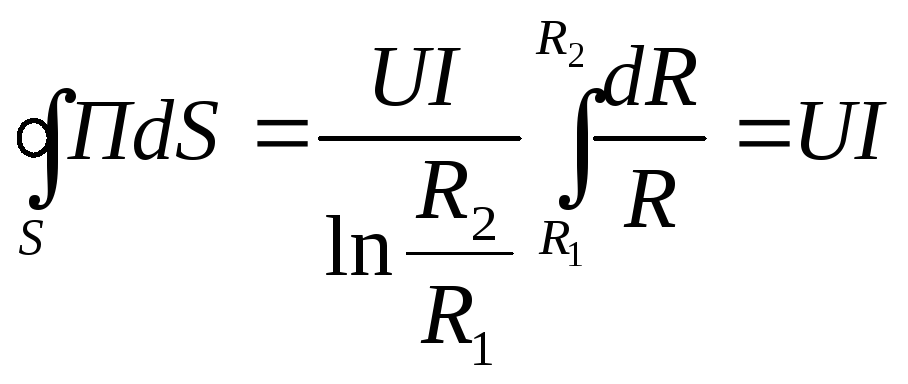
Вывод:

Получили, что вся мощность передается по диэлектрику, следовательно, энергия по жиле и оболочке не передается. Проводник (жила – оболочка), это каналы, по которым проходит ток, а так же организаторы структуры поля. Если диэлектрик не идеален, то энергия на покрытие тепловых потерь частично поступает в проводник из диэлектрика (проводимость конечна), следовательно, напряженность будет направлена по току, тогда поток вектора Пойтинга будет направлен через боковую поверхность внутрь провода.