1) Оценка значимости коэффициентов регрессии.

Найдем S, , .

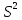= = 0,201/(8-2) = 0,0335; Отсюда S = 0,183.

= 0,1025

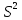= /n* = 0,0335/(8*0,1025) = 0,0408; Отсюда = 0,202.

= * = 0,0408 * 5,165 = 0,211; Отсюда = 0,459.

Проверим значимость обоих коэффициентов:

Значимость

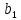: = 0

: ≠ 0

T = / = 0,713415/0,202 = 3,531

Данное значение не входит в интервал ±, следовательно, принимаем гипотезу : ≠ 0, это говорит нам о том, что коэффициент значим.

Значимость

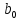: = 0

: ≠ 0

T = / = 2,557317/0,459= 5,5715

Данное значение тоже не входит в интервал ±, следовательно, принимаем гипотезу и является значимым. Этот коэффициент показывает долю пенсии.

2) Интервальные оценки коэффициентов регрессии.

Найдем доверительные интервалы.

- * ₁ + *

0,16553 1 1,2613

₁ϵ(0,16553;1,2613)

- * ₀ + *

1,312371 0 3,802263

₀ϵ(1,3124;3,8022)

Эти доверительные интервалы показывают диапазон вокруг значения наших случайных величин и , и мы можем с уверенностью 93% заявлять, что истинные значения попадут в пределы этого интервала.

3) Значимость уравнения регрессии в целом.

Мерой общего качества уравнения регрессии является коэффициент детерминации R² :

R² = 1 - е_i² / ( y_i - )² .

R² = 1 – 0,201/0,61875= 0,674501

Полученное значение показывает, что данная математическая модель, которая описывается уравнением регрессии = 2,557317 + 0,713415, на 32,5% достоверно описывает экспериментальные данные, и было использовано достаточное количество переменных.

6. Прогноз денежных доходов, направленных на прирост сбережений и доверительный интервал для нее, при значении X = = 3.

Вычислим прогнозируемое значение пенсии, при оплате труда 3 тыс. руб.

= 2,557317 + 0,713415*3 = 4,697562

= 2,7123 (уровень значимости α = 0,07, в таблицу входим со значениями: α/2 = 0,035, и ν = n – 2 = 8 – 2 = 6 степенями свободы).

Интервальный прогноз для среднего значения вычисляется следующим образом:

_р t_кр S ,

построим дополнительную таблицу:

n		-
1	1,8	-0,450	0,203
2	1,9	-0,350	0,123
3	2,4	0,150	0,023
4	2,1	-0,150	0,023
5	2,7	0,450	0,203
6	2	-0,250	0,063
7	2,6	0,350	0,123
8	2,5	0,250	0,063
9	18	0,000	0,820
Сумма	2,25	-0,450	0,203
Среднее	1,8

S = 0,183;

= 0,203.

Доверительный интервал будет заключен в [4,32339; 5,071734]. Следовательно, при прогнозируемом значении прожиточного минимума в 3 тыс. руб., мы можем спрогнозировать пенсию в размере 4,698 тыс. руб.

i	xi	yi	x2	x*y	y2	yi roof	ei	ei^2
1	1,8	3,8	3,24	6,84	14,44	3,841463415	-0,041	0,002
2	1,9	3,8	3,61	7,22	14,44	3,912804878	-0,113	0,013
3	2,4	4,1	5,76	9,84	16,81	4,269512195	-0,170	0,029
4	2,1	4	4,41	8,4	16	4,055487805	-0,055	0,003
5	2,7	4,5	7,29	12,15	20,25	4,483536585	0,016	0,000
6	2	4,3	4	8,6	18,49	3,984146341	0,316	0,100
7	2,6	4,6	6,76	11,96	21,16	4,412195122	0,188	0,035
8	2,5	4,2	6,25	10,5	17,64	4,340853659	-0,141	0,020
Сумма	18	33,3	41,32	75,51	139,23		0,000	0,201
Среднее	2,25	4,1625	5,165	9,43875	17,40375
S	0,18321319
S^2	0,033567073
b1	0,713414634				0,13140625
b0	2,557317073				0,13140625
Sb1^2	0,040935455	Sb1	0,20232512		0,00390625
Sb2^2	0,211431626	Sb2	0,45981695		0,02640625
R^2	0,674501109				0,11390625
					0,01890625
Sx	0,320156212				0,19140625
Sy	0,278107443				0,00140625
r	0,821280165				0,61875

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,821280165
R-квадрат	0,674501109
Нормированный R-квадрат	0,620251293
Стандартная ошибка	0,18321319
Наблюдения	8
Дисперсионный анализ
	df	SS		MS		F		Значимость F
Регрессия	1	0,417347561		0,417347561		12,43324251		0,012426602
Остаток	6	0,201402439		0,033567073
Итого	7	0,61875
	Коэффициенты	Стандартная ошибка		t-статистика		P-Значение		Нижние 95%		Верхние 95%		Нижние 93,0%		Верхние 93,0%
Y-пересечение	2,557317073	0,459816948		5,561598121		0,001430661		1,432185536		3,68244861		1,545232875		3,569401272
Переменная X 1	0,713414634	0,202325122		3,526080332		0,012426602		0,218342896		1,208486373		0,268085117		1,158744151
ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки
1	3,841463415	-0,041463415
2	3,912804878	-0,112804878
3	4,269512195	-0,169512195
4	4,055487805	-0,055487805
5	4,483536585	0,016463415
6	3,984146341	0,315853659
7	4,412195122	0,187804878
8	4,340853659	-0,140853659
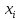