
Глава II модель множественной регрессии
2.1. Методические указания
На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. В этом случае вместо парной регрессии рассматривается множественная регрессия.
Множественная регрессия– уравнение связи с несколькими объясняющими (независимыми) переменными:
Y=f(х1,х2, …,хm), (2.1)
т.е. условное математическое ожидание имеет вид (2.1):
М(Y/х1,х2, …,хm) =f (х1,х2, …,хm). (2.2)
Теоретическое линейное уравнение регрессииимеет вид:
Y
= ![]() 0
+
0
+ ![]() 1
Х1
+
1
Х1
+ ![]() 2
Х2
+ …+
2
Х2
+ …+ ![]() m
Хm
+
m
Хm
+![]() ,
(2.3)
,
(2.3)
или для индивидуальных наблюдений i, i = 1,2,…,n:
yi
= ![]() 0
+
0
+ ![]() 1
xi1
+
1
xi1
+ ![]() 2
xi2
+ …+
2
xi2
+ …+ ![]() m
xim
+
m
xim
+![]() i
.
(2.4)
i
.
(2.4)
Как и в случае парной регрессии по выборочным данным мы можем получить только эмпирическое уравнение регрессии:
Y = b0 + b1 Х1 + b2 Х2 + …+ bm Хm + e . (2.5)
Или для индивидуальных наблюдений:
уi = b0 + b1 xi1 + b2 xi2 + …+ bm xim + ei . (2.5)
Для определения оценок b0,b1,b2, …,bmвоспользуемся матричным МНК. Представим данные наблюдений и коэффициенты в матричном виде:
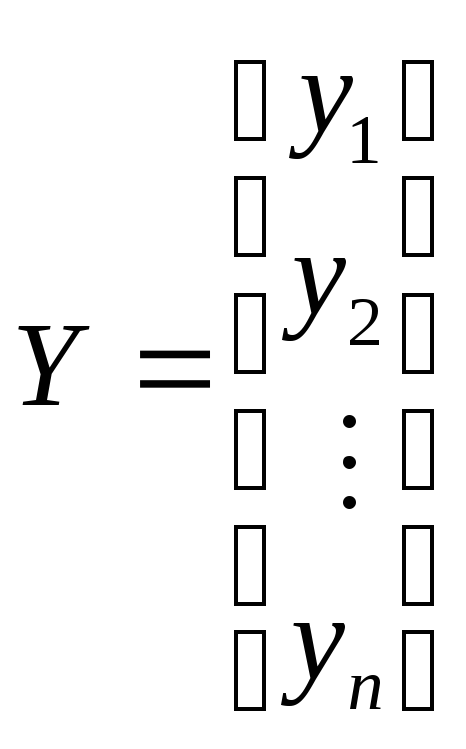 ,
,
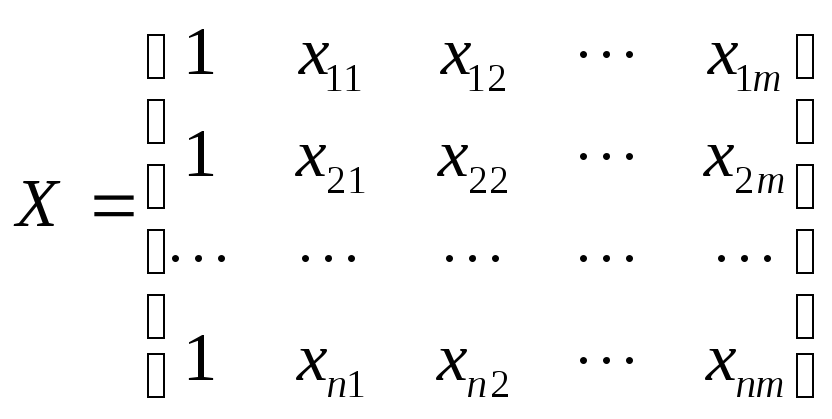 ,
,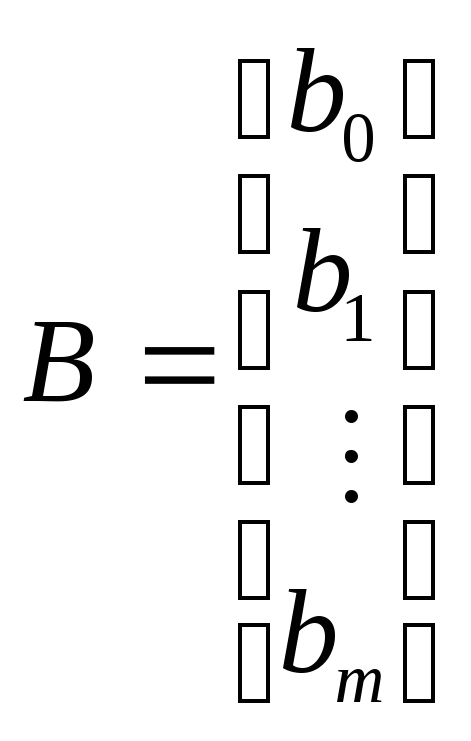 ,
,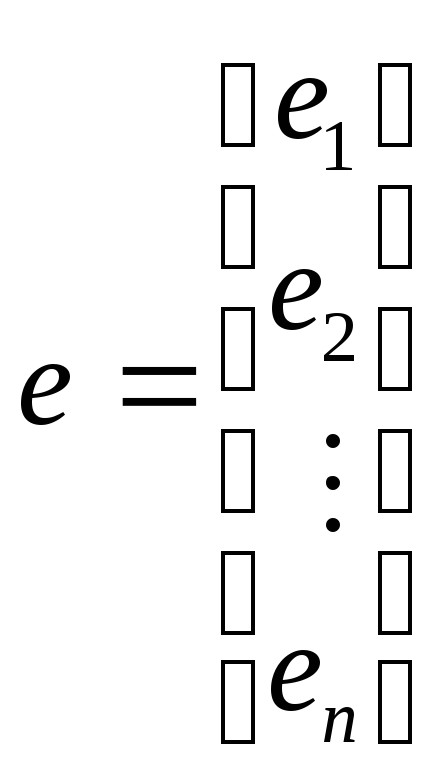 .
.
Результатом МНК будет формула вычисления коэффициентов регрессии:
B= (XT X)-1XT Y. (2.6)
Вычислим дисперсии
коэффициентов регрессии b0,b1,b2, …,bm,
которые используются для оценки их
точности, определения доверительных
интервалов для теоретических коэффициентов![]() 0,
0,![]() 1,
1,![]() 2, …,
2, …,![]() mи проверки соответствующих гипотез.
mи проверки соответствующих гипотез.
Дисперсии коэффициентов вычисляются по формулам:
![]() ,
(2.7)
,
(2.7)
В (2.7) S2– дисперсия регрессии, вычисляется по формуле:
S2= (![]() (еi2))/(n–m– 1) , (2.8)
(еi2))/(n–m– 1) , (2.8)
![]() - j-й
(j = 0, 1,…,m)
диагональный элемент матрицы
- j-й
(j = 0, 1,…,m)
диагональный элемент матрицы
Z-1= (XT X)-1. (2.9)
Проверка качества уравнения регрессии так же, как и в парной регрессии осуществляется по ряду позиций.
Проверка статистической значимости коэффициентов регрессии.
Используется критерий Стьюдента. Вычисляются Т bi=bi/Sbi,i= 0, 1, 2, …,mи сравниваются сtкрит. Результатом сравнения является вывод о значимости коэффициентов b0,b1,b2, …,bm.
Интервальные оценки коэффициентов уравнения регрессии.
Так как объем
выборки ограничен, то
b0
, b1
, b2
, …, bm
– случайные величины, поэтому желательно
найти доверительные интервалы для
истинных значений ![]() 0
,
0
, ![]() 1
,
1
, ![]() 2
, …,
2
, …, ![]() m.
Для этого также используется t
– критерий Стьюдента.
m.
Для этого также используется t
– критерий Стьюдента.
Проверка общего качества уравнения регрессии.
Для этой цели, как и в случае парной регрессии, используется коэффициент детерминации R2:
R2= 1 -![]() еi2/
еi2/![]() (yi-
(yi-![]() )2. (2.10)
)2. (2.10)
В множественной регрессии каждая новая переменная хiприводит к увеличениюR2, хотя это еще не означает, что уравнение регрессии становится более значимым. Чтобы исключить эту зависимость от числа переменных, иногда используют так называемыйскорректированный коэффициент детерминации:
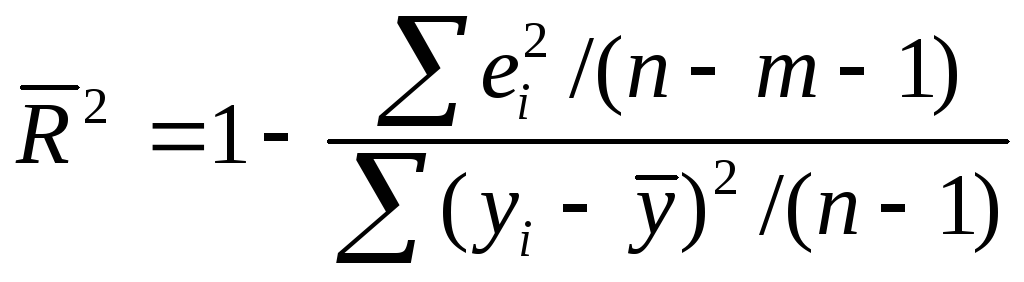 .
(2.11)
.
(2.11)
Или эту формулу можно преобразовать к виду:
![]() .
(2.12)
.
(2.12)
Анализ статистической значимости коэффициента детерминации.
По величине R2можно только предполагать насколько значимо или не значимо уравнение регрессии. Даже при небольшой величинеR2(< 0,5) не всегда следует отказываться от уравнения регрессии. Для этого необходимо проверить статистическую значимость самого коэффициента детерминации. Для чего проверяются гипотезы
Н0:R2= 0,
Н1:R2> 0.
Для проверки используется распределение Фишера. Вычисляется F– статистика:
![]() .
(2.13)
.
(2.13)
При заданном уровне
значимости
![]() по таблице критических точек Фишера
находитсяfкр,
и еслиF> fкр, тоR2статистически
значим.
по таблице критических точек Фишера
находитсяfкр,
и еслиF> fкр, тоR2статистически
значим.
Проверка выполнимости предпосылок МНК с помощью статистики Дарбина-Уотсона.
Статистическая
значимость коэффициентов регрессии и
близкое к единице значение коэффициента
детерминации R2еще не гарантируют высокое качество
уравнения регрессии. Если не выполняются
необходимые предпосылки МНК об отклонениях![]() ,
то коэффициенты регрессии и само
уравнение являются не вполне состоятельными,
а это значит что внешние признаки
«хорошего» уравнения не отвечают
действительности. Поэтому следующим
этапом проверки качества уравнения
регрессии является проверка соответствия
выборочных данных предпосылкам МНК.
Для этого воспользуемся статистикой
Дарбина – Уотсона, которая устанавливает,
в частности, наличие или отсутствие
статистической зависимости между
ошибками
,
то коэффициенты регрессии и само
уравнение являются не вполне состоятельными,
а это значит что внешние признаки
«хорошего» уравнения не отвечают
действительности. Поэтому следующим
этапом проверки качества уравнения
регрессии является проверка соответствия
выборочных данных предпосылкам МНК.
Для этого воспользуемся статистикой
Дарбина – Уотсона, которая устанавливает,
в частности, наличие или отсутствие
статистической зависимости между
ошибками![]() .
Так как истинные значения
.
Так как истинные значения![]() неизвестны,
то проверка осуществляется в отношении
оценок ошибокеi. При этом проверяется некоррелированность
соседних значенийеi.
неизвестны,
то проверка осуществляется в отношении
оценок ошибокеi. При этом проверяется некоррелированность
соседних значенийеi.
Статистика Дарбина – Уотсона DWрассчитывается по формуле:
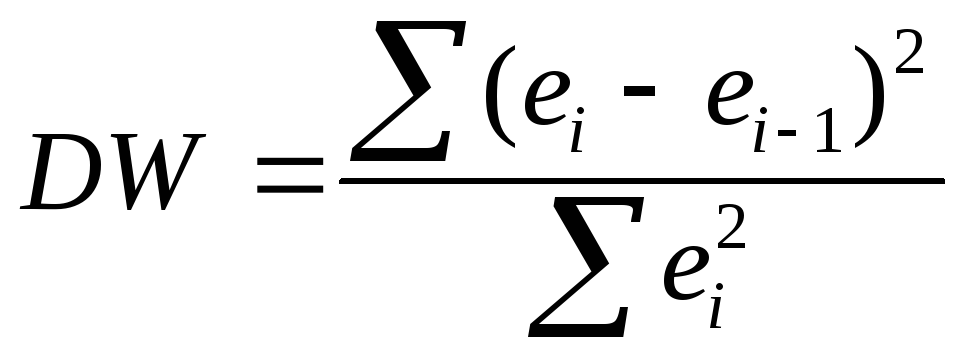 .
(2.14)
.
(2.14)
По таблицам
критических точек Дарбина – Уотсона,
входными параметрами которых являются:
n– число наблюдений;m– количество
объясняющих переменных;![]() -
уровень значимости, определяются два
числа:d1– нижняя
граница;du– верхняя граница.
-
уровень значимости, определяются два
числа:d1– нижняя
граница;du– верхняя граница.
Выводы осуществляются по следующей схеме.
Если DW<d1, то это свидетельствует о положительной автокорреляции остатков.
Если DW> 4 -d1, то это свидетельствует об отрицательной автокорреляции остатков.
При du<DW< 4 –duпринимается гипотеза об отсутствии автокорреляции остатков.
Если d1<DW<duили 4 –du<DW< 4 –d1, то остается неопределенность по вопросу наличия или отсутствия автокорреляции остатков.
В случае обнаружения признака автокорреляциинеобходимо скорректировать уравнение регрессии в соответствии с рекомендациямиГлавы IV
Прогноз значений зависимой переменной.
По аналогии с парной регрессией может быть построена интервальная оценка для среднего значения прогноза. Здесь речь идет о возможных значениях Yрпри определенных значенияхвектораобъясняющей переменнойХр.
Интервальный прогноз для среднего значениявычисляется следующим образом:
![]() р
р![]() tкрS
tкрS![]() , (2.15)
, (2.15)
где
![]() р =b0+b1x1р+b2x2р+ …+bmxmр;tкр– критическое
значение, полученное по распределению
Стьюдента при количестве степеней
свободы
р =b0+b1x1р+b2x2р+ …+bmxmр;tкр– критическое
значение, полученное по распределению
Стьюдента при количестве степеней
свободы![]() =n-m-1
и заданной вероятности
=n-m-1
и заданной вероятности![]() /2.
/2.
