06

6.

Уравнение неразрывной струи.

Течение. Движение жидкости.

Поток. Совокупность частиц в движущейся жидкости.

Линии тока.

Линия, в каждой точке которой касательная к ней совпадает по направлению с вектором скорости в данный момент времени (используется для графического изображения движения жидкости).

Трубка тока. Часть жидкости, ограниченная линиями тока.

Установившееся (стационарное) течение. Течение жидкости, при котором форма и расположение линий тока, а также значения скоростей в каждой её точке со временем не изменяются.

Уравнение неразрывности.

Рассмотри трубку тока, выбрав два сечения и , перпендикулярные направлению скорости. За время через сечение S проходит объем жидкости .

Если жидкость несжимаема, то через за 1с пройдет такой же объем жидкости¸ что и через .

или - уравнение неразрывности струи: произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для заданной трубки тока.

Уравнение Бернулли.

В стационарно текущей идеальной жидкости (в ней отсутствуют силы внутреннего трения – физическая абстракция) выбираем трубку тока, ограниченную сечениями и .

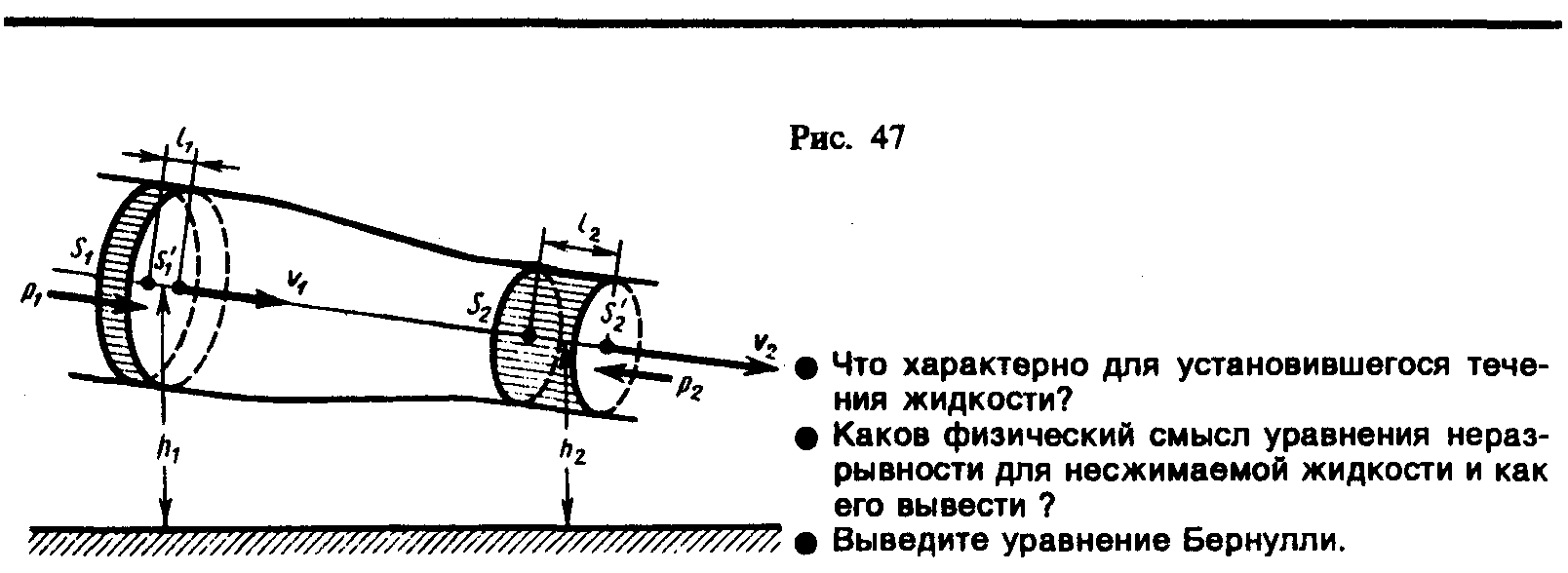
По закону сохранения энергии изменение полной энергии жидкости массой m в местах сечений и равно работе внешних сил по перемещению этой массы жидкости: (1), где

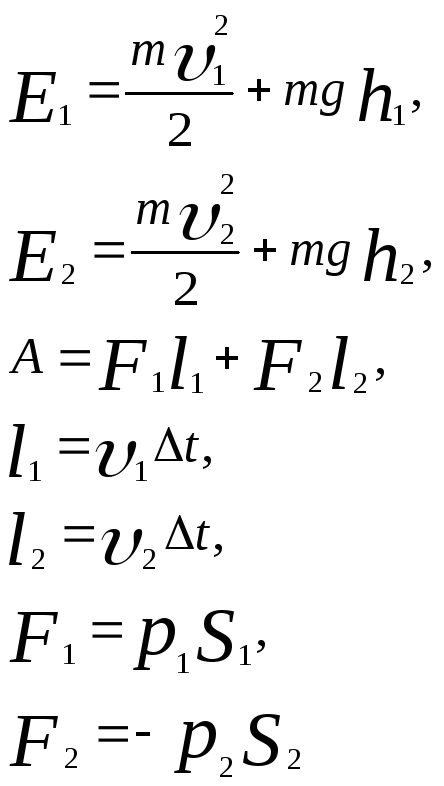
(отрицательная, так как направлена в сторону, противоположную течению жидкости)

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, . Подставив все эти формулы в (1) и разделив на , получим:

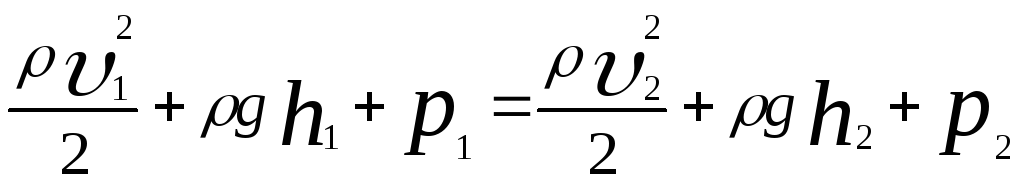, где - плотность жидкости. Сечения выбраны произвольно, поэтому

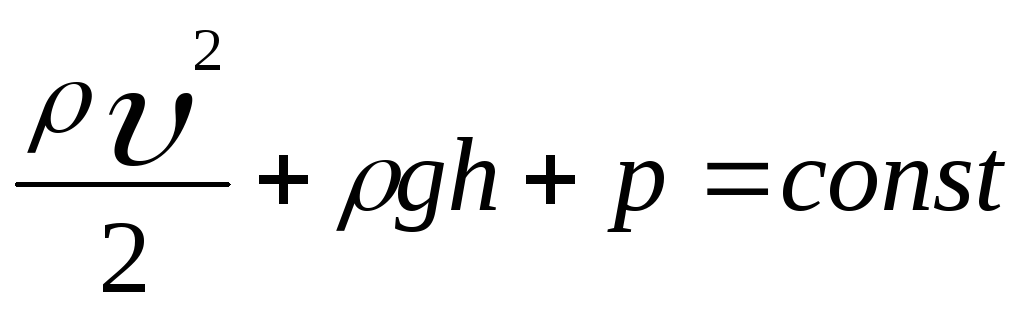- уравнение Бернулли, где p – статическое давление, - гидростатическое давление, - динамическое давление.