05

5.

Момент силы.

Момент силы относительно неподвижной точки О

Физическая величина, определяемая векторным произведением радиуса-вектора , проведенного из точки О в точку А приложении силы, на силу : .

Здесь - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

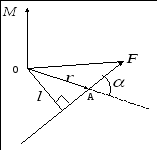
Модуль момента силы: , где -угол между и ; -кратчайшее расстояние между линией действия силы и точкой О - плечо силы.

Момент силы относительно неподвижной оси z.

Скалярная величина , равная проекции на эту ость вектора момента силы, определенного относительно произвольной точки О данной оси z. Значение момента не зависит от выбора положения точки О на оси z.

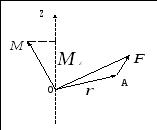
Если ось z совпадет с направлением вектора , то момент силы представляется в виде вектора, совпадающего с осью: .

Момент инерции.

Момент инерции системы (тела) относительно оси вращения есть физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

.

В случае непрерывного распределения масс эта сумма сводится к интегралу , где интегрирование производится по всему объему тела. Величина r а данном случае есть функция положения точки с координатами x, y, z.

Теорема Штейнера.

Момент инерции тела J относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс C тела, сложенному с произведением массы m тела на квадрат расстояния a между осями: .

Момент инерции однородных тел.

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиуса R Сплошной цилиндр или диск радиуса R Прямой тонкий стержень длиной l Прямой тонкий стержень длиной l Шар радиусом R	Ось симметрии То же Ось перпендикулярна стержню и проходит через его середину Ось перпендикулярна стержню и проходит через его конец Ось проходит через центр шара

Основной закон динамики вращательного движения.

Работа вращения тела идет на увеличение его кинетической энергии: ,

( - момент сил относительно оси z), 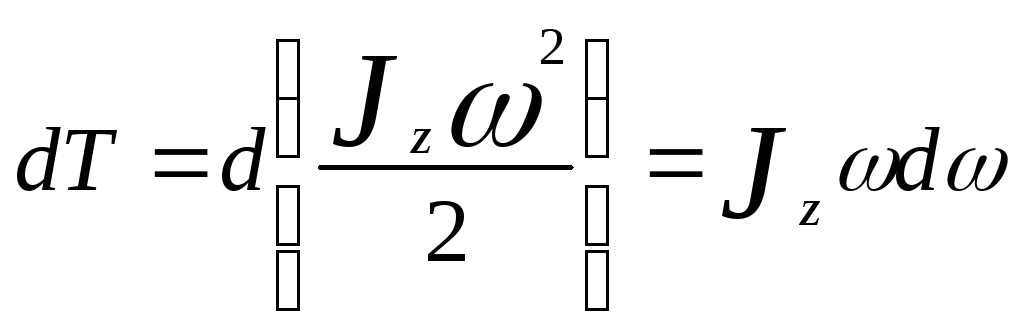. Тогда или .

Учитывая, что , получаем - уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси.

Если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство , где J – главный момент инерции тела (момент инерции относительно главной оси).

Энергия вращающегося тела.

Абсолютно твердое тело вращается вокруг неподвижной оси z. Разбивая тело на элементарные объемы массами , находящиеся от оси на расстояниях , запишем .

Поскольку , , 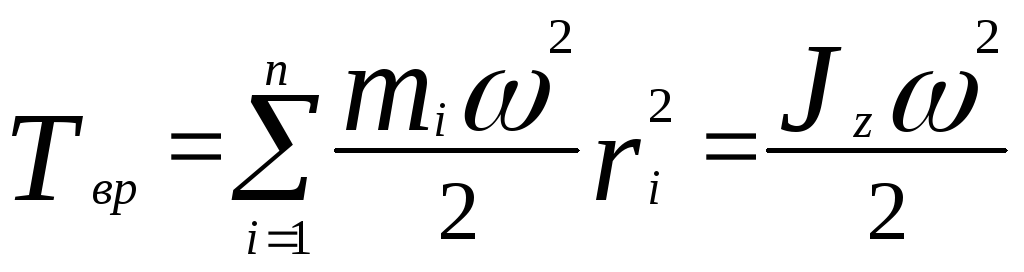где -момент инерции тела относительно оси z.

Из сравнения формул 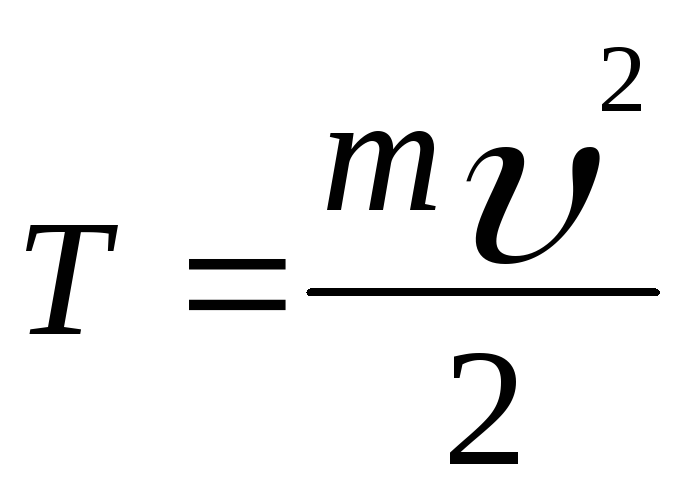и следует, что момент инерции – мера инертности тела при вращательном движении.