Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Инженерно-технологическая академия ЮФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

UML_4256

.pdf

Скачиваний:

Добавлен:

01.06.2015

Размер:

6.64 Mб

Скачать

☆

<<< < Предыдущая 26 27 28 29 30 31 32 33 34 35 36 37 38 3940 / 5040 41 42 43 44 45 46 47 48 49 50 > Следующая >>>

	σ (τ, f )− I		< ε	(4)

не зависимо от выбора точки ξi .

Определение 2. Предел интегральных сумм (3) называется кратным интегралом от функции f (x) по множеству E , то есть


∫ f (x)dx = lim		m
∫ f (x)dx = lim		∑ f (ξi )µ(Ei ).	(5)
E	δτ →0 i=1

Теорема 2. Определения 1 и 2 эквивалентны.

Доказательство. Заключим область интегрирования E в брус π% . Тогда функция F(x) (см. (1)) будет продолжением функции f (x) в

область π \ E . При таком продолжении к возможным точкам разрыва функции f (x) внутри области E добавятся возможные точки разрыва

на границе ∂E . А поскольку мера Жордана границы ∂E равна нулю, то

∫	f (x)dx = ∫ F(x)dx (см. свойство 6 в теореме 1).
E	π

Примем определение 2, то есть будем считать (5) верным. Поскольку предел интегральных сумм в (5) не зависит от способа разбиения области интегрирования, то справедливо равенство (3) в §2. А это означает, что из определения 2 следует определение 1.

Доказательство обратного утверждения (что из определения 1 следует определение 2) довольно громоздкое, поэтому примем его без доказательства. Заметим только, что фактически мы принимаем без доказательства утверждение, что мера Жордана области интегрирования не зависит от способа ее разбиения, в частности от выбора системы координат, поскольку ребра элементарных брусов мы выбираем параллельными осям координат.

§ 4. Сведение двойного интеграла к повторному

Рассмотрим сначала частный случай, когда ограниченная функция двух переменных f (x, y) задана на двумерном брусе (прямоугольнике)

π	= [a1,b1 ]×[a2 ,b2 ].	(1)
Теорема. Если функция двух переменных		f (x, y) интегрируема

на прямоугольнике (1), то есть существует двойной интеграл Римана ∫∫ f (x, y)dxdy , и для всякого фиксированного x [a1,b1 ] существует

однократный интеграл Римана

391

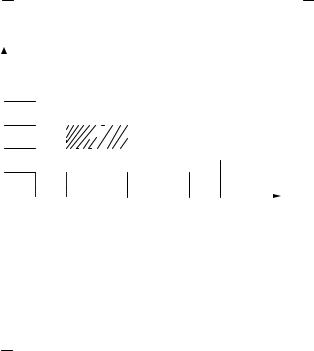
J (x)= b∫2	f (x, y)dy ,					(2)
a2
		b		b	b	f (x, y)dy , равный
то существует повторный интеграл ∫1			J (x)dx = ∫1 dx ∫2			f (x, y)dy , равный
двойному, то есть		a1		a1	a2
двойному, то есть	b	b
	b	b	f (x, y)dy .
∫∫ f (x, y)dxdy = ∫1 dx ∫2			f (x, y)dy .			(3)
π	a1	a2
Доказательство. Разобьем ребро [a1,b1 ]				на k отрезков точками
a1 = x0 < x1 < x2 < ... < xk = b1 , а ребро			[a2 ,b2 ]	на	p	отрезков точками
a2 = y0 < y1 < y2 <... < yp = b2 .	Проведем через				точки xi , y j прямые,

параллельные осям координат, получим сеточное разбиение

прямоугольника π

на

элементарные

ячейки π

ij = ∆xi ×∆y j (см.

рисунок).

π ij

yj−1

i−1

Пусть mij и	Mij		– точные		нижняя	и	верхняя грани функции
f (x, y) на ячейке π		ij . Тогда
			mij ≤ f (x, y)≤ Mij .					(4)
Зафиксируем		в	(4)	переменную		x	(положим x = ξi ,	где
ξi [xi−1, xi ] – произвольная точка) и проинтегрируем неравенство (4)
по переменной y по отрезку
по переменной y по отрезку				y j−1, y j . В результате получим
				y j	(ξi , y)dy ≤ Mij ∆y j .
		mij ∆y j ≤ ∫ f			(ξi , y)dy ≤ Mij ∆y j .			(5)
				y j−1		j , получим
Суммируя неравенства (5) по индексу						j , получим
				392

	p			p
	∑ mij ∆y j ≤ J (ξi )≤ ∑ Mij ∆y j .				(6)
	j=1			j=1
p	y j		b
p			2	f (ξi , y)dy .
Здесь J (ξi )= ∑ ∫			f (ξi , y)dy = ∫	f (ξi , y)dy .
j=1 y		j−1	a
		j−1	2
Умножим теперь неравенства (6) на ∆xi и просуммируем по
индексу i . Получим
k p			k	k p
∑ ∑ mij ∆xi ∆y j			≤ ∑ J (ξi )∆xi ≤ ∑ ∑ Mij ∆xi∆y j .		(7)
i=1 j=1			i=1	i=1 j=1

Левая и правая части неравенства (7) представляют собой нижнюю и верхнюю суммы Дарбу. И поскольку двойной интеграл существует,

то в пределе, когда		диаметр	разбиения δτ → 0,		они совпадают с
двойным интегралом		∫∫ f (x, y)dxdy . Средняя часть неравенства				(7)
		π
представляет собой интегральную сумму для функции J (x) на отрезке
[a1,b1 ]. Так как при		δτ → 0	max ∆xi → 0 , то по		теореме о «двух
милиционерах» имеем			b1
	k			J (x)dx = ∫∫ f (x, y)dxdy .
lim	∑ J	(ξi )∆xi = ∫
max ∆xi →0 i=1			a1	π
Теорема доказана.
Сведение двойного интеграла к повторному – основной способ
вычисления двойного интеграла.
Пример 1. Вычислить интеграл
	∫∫(x2 + y2 )dxdy ,			D :1 ≤ x ≤ 2, 2 ≤ y ≤ 3.
	D			f (x, y) = x2 + y2
Решение.	Функция				непрерывна	в

прямоугольнике D , следовательно, интегрируемая и удовлетворяет условиям теоремы. Воспользуемся формулой (3):

	2	3		2		1

∫∫(x2 + y2 )dxdy = ∫dx∫			(x2	+ y2 )dy = ∫	x2 y +		y3	32 dx =
						3
D	1	2		1

2			19		1			19				26

= ∫	x2	+		dx =		x3	+		x	12	=		. Ответ совпадает с результатом,
			3		3			3				3
1

полученным в примере §2.

Замечание 1. Если поменять местами x и y , то при тех же требованиях теоремы вместо (3) получим

393

	b	b
∫∫ f (x, y)dxdy = ∫2		dy ∫1 f (x, y)dx .	(8)
π	a2	a1

Замечание 2. Формулы (3) и (8) доказывают возможность менять порядок интегрирования в повторном интеграле, если требования теоремы выполняются (см. (7) в §1, гл.10).

Пусть теперь функция двух переменных f (x, y) задана на

произвольном компакте K , граница переменных которого ∂K является кусочно-гладкой кривой. Тогда граница имеет нулевую двумерную меру, поэтому сам компакт – измеримое множество. Положим, что компакт K является элементарным множеством вдоль оси y . Это

означает, что любая прямая, параллельная оси y, пересекает границу ∂K не более чем в двух точках или совпадает с границей (см. рисунок).

y	y2 (x)
b2	y2 (x)
b2
a2	y1	(x)
	y1	(x)	x
0	a1	b	x
		1

Пусть π K – брус, содержащий компакт K . В этом случае компакт можно представить в виде:

K ={(x, y) R2 : a1 ≤ x ≤ b1 ,

y1 (x)≤ y ≤ y2 (x)},

(9)

где y1 (x) и y2 (x) – кусочно-гладкие функции.

Сведем и в этом случае двойной интеграл по компакту K к повторному интегралу.


(π	Пусть прямоугольник π	= [a1,b1 ]×[a2 ,b2 ] содержит компакт K
	K ) и пусть функция		(x, y) K,
	F (x, y)= f (x, y),

	0,		(x, y) π \ K.

394

Если функция F (x, y)

удовлетворяет требованиям теоремы, то

справедлива формула (3),

которая

для

функции

f (x, y)

согласно

определению 1 §3 запишется так:

∫∫ f

(x, y)dxdy =∫∫F (x, y)dxdy =

y (x)

(x, y)dy.

= ∫1 dx ∫2 F (x, y)dxdy = ∫1 dx

2∫

(10)

y1(x)

Замечание

3. Если

компакт

–

элементарное множество в

направлении оси x , то есть его можно представить в виде

{

}

K = (x, y) R2

: a

≤ y ≤ b , x (y)≤ x ≤ x

(y) ,

(11)

то вместо формулы (10) будем иметь

(y)

f (x, y)dx .

∫∫

f (x, y)dxdy = ∫2 dy

2∫

(12)

x1(y)

Пример 2. Найти площадь фигуры D , ограниченной кривыми:

(x −1)2 + y2 =1, y = 2

x, x = 2 (см. рисунок).

Решение. Согласно следствию §3 имеем

2 x

µ(D)= S = ∫∫ dxdy =∫dx

∫

dy =

1−(x−1)2

−(x −1)

= ∫

2 x − 1

dx =

2 − π .

x3 −

−1)

1−(x −

1)2 −

arcsin (x −1)

02 =

Замечание 4. Если компакт K не является элементарным в направлении осей координат, но его можно представить в виде конечного объединения элементарных компактов, не имеющих общих

	m
внутренних точек K =U Ki , µ(Ki ∩ K j )= 0, i ≠		j ,
	i=1
то воспользовавшись свойством аддитивности интеграла, получим
	m
∫∫ f (x, y)dxdy =∑ ∫∫ f (x, y)dxdy .			(13)
K	i=1 Ki

395

§5. Сведение кратного интеграла к повторному (общий случай). Теорема Фубини

Представим

n -мерный брус

=[a1,b1 ]×[a2 ,b2 ]×...×[an ,bn ],

где

[ai ,bi ]={ai ≤ xi ≤ bi ,i =1,2,...,n},

виде

прямого

произведения

двух

брусов

π = π1 ×π2 ,

где

π1 = a1,b1 × a2 ,b2 ×...× am ,bm

π2 = am+1,bm+1 ×...× an ,bn . Брус π1 R

называют проекцией бруса

на

координатное подпространство

точек

u = (x1, x2 ,..., xm ),

брус

2 Rn−m

–

проекцией

бруса

на

подпространство

точек

v = (xm+1, xm+2 ,..., xn ).

Обозначим точку x = (x1, x2 ,..., xn )= (u,v). Тогда функцию

f (x) n

переменных

можно

считать

функцией

двух

переменных

u,v, f (x) = f (x1, x2 ,..., xm , xm+1,..., xn )= f (u,v) .

Теорема (Фубини). Пусть функция

f (x)= f (u,v)

определена и

ограничена на брусе π

= π1 ×π

2 . Если функция

f (u,v) интегрируема на

брусе π

и при любом фиксированном u π1

интегрируема на брусе π

2 ,

при

любом

фиксированном

v π

интегрируема на

брусе

π1,

то

справедлива формула

∫

f (x)dx = ∫

f (u,v)dudv = ∫ du ∫ f (u,v)dv = ∫

dv ∫ f (u,v)du .

(1)

π1

Доказательство теоремы совпадает с доказательством аналогичной

теоремы для двойного интеграла (см. §4).

Если

частности

π1 = [a1,b1 ],

то

есть

m =1,

функция

f (x)= f (x1, x2 ,..., xn )

удовлетворяет требованиям теоремы Фубини, то

из (1) получим

f (x1, x2 ,..., xn )dx2dx3...dxn .

∫

f (x)dx = ∫1 dx1 ∫

(2)

2 = [a2 ,b2 ]×π

Если в свою очередь π

3 , то применяя формулу (1) к

внутреннему интегралу (2), получим

f (x1, x2 ,..., xn )dx3dx4 ...dxn .

∫

f (x)dx = ∫1 dx1 ∫2 dx2 ∫

(3)

Продолжая

этот

процесс

(n −1)

раз,

окончательно

получим

следующую формулу:

396

		b	b	b
	∫ f (x)dx = ∫1 dx1 ∫2			dx2 ... ∫n f (x1, x2 ,..., xn )dxn .		(4)
	π	a1	a2	an
	Таким образом интегрирование функции n переменных по брусу
π	сводится к n -кратному интегрированию по отрезку.
	Пусть теперь ограниченная функция f (x)				задана на некотором
компакте K Rn , граница которого ∂K имеет					n -мерную меру нуль.
Предположим также, что компакт K – множество связное выпуклое
(см.§2, гл.9).		[a1,b1 ]	– проекция компакта K на координатную
	Пусть отрезок
ось Ox1 . При этом a1		= min x1,b1 = max x1, x = (x1, x2 ,..., xn ).
		x K		x K	точку x1 =ξ1 [a1,b1 ]
	Через произвольную,		но фиксированную


проведем плоскость, перпендикулярную оси Ox1 , и рассмотрим сечение
компакта K , то есть множество точек K1 ={(ξ1, x2 , x3 ,..., xn ) K}.
	Поместим компакт	K в брус π		= [a1,b1	]×π	2 , где	брус
π	2 =[a2 ,b2 ]×...×[an ,bn ] и π	2 K1 при любом ξ1 [a1			,b1 ].
	Рассмотрим функцию	F (x)= f (x), x K1 . Если функция					F (x)
		0, x π	\ K

удовлетворяет условиям теоремы Фубини, то согласно (1) и определению 1 §3 имеем

∫ F (x)dx = ∫		b
∫ F (x)dx = ∫		f (x)dx = ∫1 dx1 ∫ F (x)dx2 ...dxn =
π	K	a1 π	2
b	∫ f (x1, x2 ,..., xn )dx2...dxn .
= ∫1 dx1	∫ f (x1, x2 ,..., xn )dx2...dxn .			(5)
a1	K1

Применим теперь теорему Фубини к внутреннему интегралу равенства (5). Для этого компакт K1 спроектируем на координатную ось

Ox2 . Эта проекция будет отрезком, длина которого зависит от выбора

точки

x =ξ

[

a ,b

]

. Пусть

a (x ),b

(

проекция K

на ось Ox .

1 1

2 1 2

1 )

Через

произвольную,

но

фиксированную

точку

x =ξ

(x ),b (x ) проведем плоскость,

перпендикулярную оси

Ox2 ,

и рассмотрим

сечение

компакта

K1 ,

то

есть множество точек

K2 ={(ξ1,ξ2 , x3 ,..., xn ) K1}.

397

Произведя все дальнейшие операции, которые выполняли при получении формулы (5), получим

∫ f (x)dx = ∫ dx1

b2 (x1 )	dx2 ∫ f (x1, x2 ,..., xn )dx3...dxn .	(6)
∫	dx2 ∫ f (x1, x2 ,..., xn )dx3...dxn .	(6)
a2 (x1 )	K2

Продолжая этот процесс, окончательно получим

	b1	dx1	b2 (x1 )	dx2	b3 (x1,x2 )		bn (x1,...,xn−1 )		f (x1, x2 ,..., xn )dxn . (7)
∫	f (x)dx = ∫		∫		∫	,x2 )	dx3...	∫
K	a1		a2 (x1 )		a3 (x1		an (x1 ,...,xn−1 )

На практике поступают иначе. Чтобы свести кратный интеграл ∫ f (x)dx к повторному, проектируют множество K на координатную

K
плоскость xn = 0 . (Пусть Kx					искомая проекция). Через произвольную
		Kx			n
точку проекции		Kx	проводят прямую, параллельную оси Oxn .							Будем
			n
считать, что она пересекает ∂K в двух точках x1n = an (x1, x2 ,..., xn−1 ) и
x2n = bn (x1, x2 ,..., xn−1 ).				Тогда		K = [x1n , x2n ]× Kx		для	всякой	точки
(x1, x2 ,..., xn−1 ) Kx							n
(x1, x2 ,..., xn−1 ) Kx			, а из теоремы Фубини следует
		n				bn (x1,x2 ,...,xn−1 )
	∫ f (x)dx =	∫ dx1dx2 ...dxn−1				bn (x1,x2 ,...,xn−1 )	f (x1, x2 ,..., xn )dxn .			(8)
	∫ f (x)dx =	∫ dx1dx2 ...dxn−1				∫	f (x1, x2 ,..., xn )dxn .			(8)
	K	Kx				an (x1,x2 ,...,xn−1 )
		n		Повторяя этот процесс, мы вновь получим
Z	V			Повторяя этот процесс, мы вновь получим
Z				формулу (7).
				формулу (7).
				Запишем формулу (8) для частного случая,
				когда n = 3 , то есть для тройного интеграла
				∫∫∫ f (x, y, z)dxdydz = ∫∫ dxdy				Z2 (x, y)	f (x, y, z)dz .(9)
				∫∫∫ f (x, y, z)dxdydz = ∫∫ dxdy				∫	f (x, y, z)dz .(9)
		Y		V			Dxy	Z1(x, y)
				Здесь V – область интегрирования, Dxy – ее
X				проекция на плоскость z = 0 (см. рисунок).
X				Если область V выпуклая, то проектируя ее
				на плоскости x = 0			и y = 0, получим еще две

аналогичные формулы:

∫∫∫ f (x, y, z)dxdydz = ∫∫ dydz			x2	(y,z)
∫∫∫ f (x, y, z)dxdydz = ∫∫ dydz				∫ f (x, y, z)dx =
V		Dyz	x1	(y,z)
= ∫∫	y2	(x,z)
= ∫∫	dxdz	∫ f (x, y, z)dy .		(10)
Dxz	y1	(x,z)
		398

Здесь Dyz

Dxz – проекции области V на плоскости x = 0 и

y = 0 соответственно.

I = ∫∫∫(1+ x)dxdydz ,

Пример

Вычислить

если

область

ограничена параболоидом z = x2 + (y −1)2

и плоскостью 2 y + z = 2 (см.

рисунок).

формулой (9). Чтобы найти Dxy ,

Решение.

Воспользуемся

исключим из уравнений параболоида и

плоскости

переменную

z .

результате

получим

2 − 2 y = x2 + (y −1)2 x2 + y2 =1,

то

есть

Dxy

–

круг,

граница

которого

x2 + y2 =1. Границей ∂V области V является

часть параболоида и плоскости. Прямая,

параллельная оси z , пересекает

∂V в двух

точках:

= x2 + (y −1)2 и z

= 2 − 2 y .

Согласно (9) получим

2−2 y

I = ∫∫

(1+ x)dxdy

dz = ∫∫

(1+ x)(1− x2 − y2 )dxdy .

∫

Dxy

x2 +(y−1)2

Dxy

Получили двойной интеграл, который можно вычислить по формулам (10) или (12) предыдущего параграфа. В нашем случае

получим

I = ∫∫

((1+ x)(1− x2 )−(1+ x)y2 )dxdy =

Dxy

1−x2

(

)

∫ dx ∫

(1+ x)(1− x2 )−(1+ x)y2

dy =

∫ (1+ x)(1

− x2 )

dx =

−1

− 1−x

−1

x = sin t

∫2 (1+sin t )cos4 tdt = π .

dx = costdt

3 −π2

Пример 2. Найти объем 4-мерного шара

+ x2

≤ r2 , r = const .

(11)

Решение. Шар – множество выпуклое. Воспользуемся формулой

(8). Проекцию Kx

получим из неравенства (11), положив в нем x4 = 0 .

x2 + x2 + x2 ≤ r2 – шар в пространстве R3 . Точки

В результате получим

399

пересечения прямой, параллельной

оси x4 ,

границей шара

будут

= ± r2 − x2 − x2

− x2 .

Согласно

формуле

(8) и

следствию

§3

запишем

r2 −x2 −x2 −x2

µ(K )=V = ∫ dx =

dx1dx2dx3

∫∫∫

∫

dx4 =

x12 +x22 +x32 ≤r2

−

r2 −x2

−x2

= 2

∫∫∫

r2 − x12 − x22 − x32 dx1dx2dx3.

+x2 +x2 ≤r2

Получили

тройной интеграл,

который

можно

вычислить

по

формулам (9) или (10). Используя формулу (9) и табличный интеграл

∫

2 − x2 dx =

a2 − x2 +

a2 arcsin

получим

r2 −x2

−x2

dx1dx2

2 − x12 − x22 − x32 dx3 =

V = 2 ∫∫

∫

x12 +x22 ≤r2

− r2 −x2 −x2

= π ∫∫

(r2 − x12 − x22 )dx1dx2 .

+x2

≤r2

Получили

двойной

интеграл, который

можно

вычислить по

формулам (10) или (12) предыдущего параграфа. Воспользуемся первой формулой

V = π ∫

dx1

r2 −x2

(r2 − x12 − x22 )dx2

∫

= 4 π ∫ (r2 − x12 )2 dx1

−r

−

r2 −x

3 −r

x1 = r sin t

+ cos 2t 2

dx1 = r cost

∫ r

cos

tdt =

πr

∫

dt =

1+ cos 4t

πr4

π 2r

4 .

∫

1+ 2cos 2t +

Упражнение. Вычислить объем пирамиды в четырехмерном

пространстве

≤1, x ≥ 0,i =1,2,3,4 .

α1

α2 α3 α4

Ответ:

α α α α

400

<<< < Предыдущая 26 27 28 29 30 31 32 33 34 35 36 37 38 3940 / 5040 41 42 43 44 45 46 47 48 49 50 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025169.98 Кб0Uchebnoe_posobie_FBFO_1-2_kurs_2003g.docx
#
05.09.2019687.71 Кб18Uchebnoe_posobie_metrologia.docx
#
01.06.20152.46 Mб17UMK_po_Menedzhmentu_modul_2.pdf
#
01.06.2015359.44 Кб8umk_treb.pdf
#
01.06.2015903.17 Кб15UML_1321.pdf
#
01.06.20156.64 Mб26UML_4256.pdf
#
01.06.2015321.05 Кб16UML_4497.pdf
#
01.06.20151.11 Mб9UML_4562.pdf
#
01.06.2015641 Кб10UML_4564.pdf
#
01.06.2015943.33 Кб9UML_4597.pdf
#
01.06.20151.72 Mб72UML_4797.pdf