
UML_4256
.pdf
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax |
|
|
|
= λ |
|
x |
|
, |
|
|
(9) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где λ = (∑ ∑ aij2 ) = |
|
A |
|
|
|
– евклидова норма матрицы оператора A. |
|||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
i =1 j =1 |
|
|
|
|
|
|
Ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя следствие 2, из (9) получим |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
≤ λ = |
|
|
|
A |
|
|
|
E . |
(10) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Если элементы |
|
aij |
|
|
|
= aij(t) |
|
|
матрицы оператора A непрерывные в |
||||||||||||||||||||||||||||
точке t0 функции параметра t , |
то ρ( A(t), A(t0)) = |
|
A(t) − A(t0) |
|
|
|
< ε при |
||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ε |
t −t0 <δε . Тогда из (10) следует непрерывность линейного оператора A по норме, определенной формулой (1).
§ 17. Обратимость линейного оператора
Если линейный оператор A отображает линейное пространство X на X и при этом взаимно-однозначен, то его называют обратимым.
Обратный оператор B = A−1 определяется равенством A−1 ( Ax) = xx X . Очевидно, в этом случае A(A−1x)= x .
Теорема 1. Линейный оператор A на конечномерном векторном пространстве X обратим тогда и только тогда, когда множество его значений совпадает со всем X .
Доказательство. Если {x1, x2,..., xn} – базис пространства X , то
n
множество всех линейных комбинаций векторов x = ∑ci xi совпадает с
i=1
X . В силу линейности оператора A множество всех его значений Ax –
n
это множество линейных комбинаций векторов ∑ci Axi . Если докажем,
i=1
что множество V ={Ax1, Ax2,..., Axn} является базисом пространства X
только в том случае, когда оператор A взаимно-однозначный, докажем теорему.
Пусть оператор A взаимно-однозначный. Докажем, что V – базис. От противного. Пусть V не является базисом, то есть
n
∑ci Axi =θ (1)
i=1
342

|
n |
|
и не все ci равны нулю. Перепишем (1) так: A(∑ci xi) |
=θ . => |
|
|
i=1 |
|
n |
A взаимно-однозначный, то нулевому вектору |
|
∑ci Axi =θ , поскольку |
||
i=1 |
|
|
|
n |
|
соответствует только |
нулевой. Но ∑ci Axi =θ |
означает, что |
|
i=1 |
|
{x1, x2,..., xn} не является базисом. Получили противоречие,
следовательно, V – базис.
Пусть теперь V – базис, докажем, что A взаимно-однозначный
n
оператор. Если V – базис, то из ∑ci Axi =θ => c1 = c2 =... = cn = 0. А из
i=1
n
равенства Ax = A(∑ci xi) =θ следует x =θ , то есть прообраз нулевого
i=1
вектора – вектор нулевой. Пусть Ax1 = Ax2 , то есть образы равны, тогда A(x1 − x2 ) =θ . => x1 = x2 , то есть равны и прообразы. Это означает
взаимную однозначность отображения A. Теорема доказана.
Теорема 2. Пусть Ω – множество всех обратимых линейных операторов, действующих из Rn в Rn .
1)Если A Ω, 
 A−1
A−1
 < α1 , B L(Rn ) и
< α1 , B L(Rn ) и 
 B − A
B − A
 = β <α , то B Ω, то есть оператор B обратим.
= β <α , то B Ω, то есть оператор B обратим.
2)Ω – открытое подмножество пространства L(Rn ) .
3)Отображение A ↔ A−1 непрерывно на Ω.
Доказательство. Напомним следствие 1 §16
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax |
|
≤ |
|
x |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
и неравенство треугольника |
|
|
|
a +b |
|
|
|
|
≤ |
|
|
a |
|
+ |
|
b |
|
. |
|
|
При a + b = c |
имеем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
c |
|
≤ |
|
c −b |
|
|
+ |
|
b |
|
|
|
или |
|
|
|
|
c −b |
|
|
|
≥ |
|
|
c |
|
|
− |
|
|
|
b |
|
. |
|
|
|
(2) |
|
|
|
|
|
|
|
|
1) |
1 |
|
|
|
|
|
(3) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
1. Поскольку x = A−1( Ax) , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
x |
= |
A−1( Ax) |
≤ |
|
|
A−1 |
|
|
Ax |
= |
|
|
|
Ax |
. |
(4) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
α |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4),1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(α − β) |
|
x |
|
|
=α |
|
x |
|
− β |
|
x |
|
|
Ax |
|
|
− |
|
|
|
|
|
|
B − A |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
Ax |
|
− |
|
(B − A)x |
|
= |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
343 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||

|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|||||
= |
Ax |
− |
Bx − Ax |
= |
Ax |
− |
Ax − Bx |
≤ |
Ax |
−( |
Ax |
− |
Bx |
) = |
Bx |
. |
||||||||
|
Итак, |
|
Bx |
|
≥ (α − β) |
|
x |
|
. |
(5) |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
Покажем, что из (5) следует обратимость оператора B , то есть его взаимная однозначность. От противного. Пусть одному образу
отвечают два разных прообраза, то есть Bx1 = Bx2 , но x1 ≠ x2 . Тогда
B(x1 − x2 ) =θ . => |
|
B(x1 − x2 ) |
= 0 . А |
по формуле (5) |
получается |
|||||||||
|
B(x1 − x2 ) |
|
= (α − β) |
|
x1 − x2 |
|
, то есть |
0 ≥ (α − β) |
|
x1 − x2 |
|
. |
Получили |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
противоречие, которое и доказывает первую часть теоремы 2.
2. По условию теоремы 
 B − A
B − A
 <α B, A Ω или ρ(B, A) <α = ε , то
<α B, A Ω или ρ(B, A) <α = ε , то
есть любой обратимый оператор принадлежит множеству Ω вместе с некоторой окрестностью. А это и означает открытость множества Ω. И утверждение 2) теоремы доказано.
3. Если y = Bx, то x = B−1y . Учитывая это, перепишем (5) так:
(α − β) B−1y ≤ BB−1 y = y y Rn .
Тогда (α − β) sup B−1y ≤ sup y =1.
|
|
|
|
|
|
|
|
|
B |
≤ 1 |
|
|
|
y |
|
≤ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
B−1 |
|
|
|
|
|
B−1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Или (α − β) |
|
|
|
|
≤1, |
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
(6) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
α − β |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Легко проверить тождество |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B−1 − A−1 = B−1 (A − B)A−1 . |
|
|
|
(7) |
|||||||||||||||||||||||||||||
Дважды используя следствие 3 §16, найдем |
A−1 |
|
≤ |
1 |
β 1 . (8) |
|||||||||||||||||||||||||||||||||||||||||
|
|
B−1 − A−1 = B−1( A − B) A−1 |
|
≤ |
B−1 A − B |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6),1) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α − β |
α |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A − B |
|
|
|
|
|
|
|
A−1 − B−1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Из (8) видно, что при |
|
|
|
= β → 0 |
|
|
→ 0 , что и означает |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
непрерывность взаимно-однозначного отображения A ↔ A−1. Теорема доказана.
§ 18. Обратимость отображения. Производная обратной функции
Определение. Дифференцируемое отображение f (x) открытого множества X Rn в Rm называется непрерывно дифференцируемым на
344

X , если f '(x) – непрерывное отображение X в линейное пространство
L(Rn , Rm ).
Определение означает, что |
x X |
и ε > 0 существует δε > 0 |
|||||||||||||
такое, что |
|
f '(x') − f '(x) |
|
|
|
< ε , если |
|
|
|||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
x'− x |
|
<δ ε , x' X . |
(1) |
||
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема 1. Отображение |
f (x) |
будет |
непрерывно |
||||||||||||
дифференцируемым на |
|
|
|
X тогда и только тогда, когда все частные |
|||||||||||
производные |
∂f i(x) |
|
, |
|
|
|
i =1,2,..., m, |
j =1,2,..., n |
существуют и |
||||||
∂x j |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
непрерывны на X . |
|
|
|
|
|
|
|
|
|
Пусть f (x) |
|
||||
Доказательство. |
Необходимость. |
– непрерывно |
|||||||||||||
дифференцируемое отображение, то есть выполняется (1). В стандартных базисах пространств Rn и Rm оператор f '(x) представляется матрицей, j -й столбец которой f '(x)e j представляет
собой частные производные ∂f i , i =1,2,...m . Согласно следствию 1 §16
∂x j
имеем
|
f '(x')e j − f '(x)e j |
|
≤ |
|
f '(x') − f '(x) |
|
1(1)≤ε при |
|
x'− x |
|
< δ ε . |
(2) |
||
|
|
|
|
|
|
|||||||||
Неравенство |
(2) означает, |
что j -й столбец матрицы |
f '(x) |
|||||||||||
непрерывный, |
следовательно, |
непрерывны все его составляющие, то |
||||||||||||
есть частные производные ∂f i . Необходимость доказана.
∂x j
Достаточность. В §8 (теорема1) достаточность доказана для частного случая числовой функции, то есть для одной строки матрицы f '(x) . Считая это доказательство верным для любой i -й строки
матрицы, получим, что все элементы матрицы f '(x) – непрерывные функции. Тогда из (10) §16 следует, что оператор f '(x) непрерывный.
Теорема доказана.
Пусть векторная функция векторного аргумента y = f (x) отображает множество Χ на множество Υ, Χ Rn , Y Rm . Возникает вопрос, при каких условиях существует обратная функция x = f −1( y) , то есть однозначное отображение множества Υ на Χ или хотя бы
345
некоторой окрестности точки b = f (a) в Χ. Если, в частности, y = f (x)
– линейная функция, то есть |
y = Ah , |
|
(3) |
||||||||||
|
|
A =[a |
|
] |
|
|
|
||||||
где h = x − a , |
ij |
|
= f '(x) |
|
– |
матрица Якоби, составленная |
из |
||||||
|
|
|
|
m×n |
|
|
|
|
|
|
|
||
чисел, то в развернутом виде получим систему линейных уравнений |
|
|
|||||||||||
y1 = a11h1 + a12h2 +... + a1nhn, |
|
|
|||||||||||
|
|
= a21h1 + a22h2 +... + a2nhn, |
|
|
|||||||||
y2 |
(3’) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
................................................ |
|
|
|||||||||||
y |
m |
= |
am1h1 |
+ |
am2h2 |
+... |
+ |
|
. |
|
|
||
|
|
|
|
|
amnhn |
|
по |
||||||
Итак, как из системы (3’) |
однозначно определить числа h j |
|
|||||||||||
известным числам yi . |
Из линейной алгебры известно, что для этого |
||||||||||||
матрица [ A] должна быть обратимой (а для этого необходимо m = n).
Если матрица A обратима, то (3’) разрешимо и h = A−1y или hi = |
|
∆i |
|
||||||||||||||
|
det A |
||||||||||||||||
– формулы Крамера. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
y = f (x) |
не |
||||||
Если |
непрерывно |
дифференцируемое |
отображение |
||||||||||||||
является линейным, то, выделив линейную часть, запишем |
|
|
|
|
|
||||||||||||
|
|
|
f (x) = f (a) + f '(a)h + o(h) . |
|
|
|
|
|
(4) |
|
|||||||
Естественно предположить, что отображение (4) будет иметь |
|||||||||||||||||
обратное отображение, если обратим оператор |
A = f '(a) . Уточнение |
||||||||||||||||
этого утверждения дает следующая теорема. |
|
|
|
|
|
|
|
|
|||||||||
Теорема 2. Пусть |
f (x) |
|
|
непрерывно |
дифференцируемое |
||||||||||||
отображение открытого множества Χ Rn |
в пространство Rn . |
Пусть |
|||||||||||||||
линейный |
оператор |
f '(a) обратим при |
некотором |
a Χ и |
пусть |
||||||||||||
b = f (a) . Тогда существуют окрестности U и V точек a и b |
такие, |
||||||||||||||||
что:1) |
отображение |
f (U ) =V |
взаимно-однозначно, |
то |
есть, |
|
если |
||||||||||
y = f (x), |
x U , то существует отображение x = f −1( y) , |
y V |
такое, |
||||||||||||||
что |
f −1( f (x)) = x |
x U ; 2) |
|
|
отображение |
f −1( y) |
непрерывно |
||||||||||
дифференцируемое в окрестности V . |
|
|
|
|
|
|
|
|
|||||||||
Доказательство. Пусть f '(a) = A. Выберем λ так, чтобы |
|
|
|
|
|||||||||||||
|
|
|
|
|
A−1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4λ |
|
|
=1. |
|
|
|
|
|
|
(5) |
|
||
Поскольку |
f (x) непрерывно дифференцируемое отображение, |
то |
|||||||||||||||
существует открытый шар U с центром в точке a такой, что |
|
|
|
|
|||||||||||||
|
|
|
|
|
346 |
|
|
|
|
|
|
|
|
|
|
||

К последнему равенству применим оператор B . Получим
(11) |
|
|
|
|
|
|||
Bl = B( f '(x)h + o(h)) = h + B(o(h)) = g( y + l) − g( y) + B(o(h)) . |
(12) |
|||||||
Из (10) следует |
|
|||||||
|
l |
|
> 2λ |
|
h |
|
. |
(13) |
|
|
|
|
|||||
Из (13) видно, что при l → 0 h → 0 , то есть отображение g( y) = f −1( y)
непрерывно. При этом |
B(o(h)) |
≤ |
|
|
|
B |
|
|
|
|
|
o(h) |
|
|
→ 0 при l → 0 . |
|
|||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
(2),(13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
2λ |
|
h |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Тогда (12) можно переписать так: |
|
|
|
g(l + h) − g( y) = Bl − o(l) . Это |
и |
||||||||||||||||||||||
означает |
дифференцируемость |
|
|
|
функции |
g( y) = f −1( y) , |
а |
||||||||||||||||||||
B = g '( y) = ( f −1( y))' = ( f '(x))−1 . По аналогии с производной обратной
функции одного аргумента последнее равенство условно записывают так:
|
−1 |
1 |
|
|
( f |
( y))' = |
|
. |
(14) |
f '(x) |
Непрерывность оператора g '( y) = ( f −1(x))' следует из непрерывности оператора f '(x) и утверждения 3) теоремы 2 §17.
Теорема доказана. |
|
|
|
Замечание. Определитель оператора f '(x) |
называют якобианом и |
||
обозначают J f (x) = det f '(x) = |
D( f 1, f 2,..., f n) |
. |
Условие обратимости |
|
|||
|
D(x1, x2,..., xn) |
|
|
оператора f '(x) в точке x = a запишется так: J f (a) = det f '(a) ≠ 0.
Пример. f (x) = ( f 1, f 2) = (u,v) , u = x2 + y2 , v = 3x2 − y2 .
Найти производную обратной функции в точке x0 = (1,1) или y0 = (2,2) .
u 'x |
u 'y |
= |
2x |
2 y |
. => |
|
Решение. f '(x) = |
|
|
|
|
||
|
|
|
6x |
|
||
v'x |
v'y |
|
|
−2 y |
|
|
J f = det f '(x) = |
2x |
2 y |
= −16xy . Следовательно, |
данная функция |
|
6x −2 y |
|
|
|
имеет обратную |
на всей плоскости, исключая |
оси координат. |
||
g '( y) = ( f '(x))−1 =(обратная матрица для матрицы f '(x) )=
348
|
|
|
−2 y −2 y |
x'u |
x'v |
x'u = |
1 |
= |
1 |
|
, |
x'v = |
1 |
|
= |
1 |
|
, |
|
|||||||
|
1 |
|
8x |
8 |
|
|
|
8 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
8x |
|
|
|
|
|||||||||||||
= − |
|
|
|
= |
y ' |
y ' |
|
. => |
3 |
|
|
3 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
16xy |
−6x 2x |
|
v |
y 'u = |
|
= |
, |
y 'v = − |
|
= − |
. |
||||||||||||||
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
8y |
|
8 |
|
8y |
8 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
||||
Итак, производная обратной функции в точке (2,2) равна |
|
|
3 |
|
|
. |
|
|||||||||||||||||||
8 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
||||||
|
Упражнение. Выразить x и y через u и v . Найти все частные |
|||||||||||||||||||||||||
производные функций x(u,v) и y(u,v) и |
|
сравнить |
результат с |
|||||||||||||||||||||||
полученным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
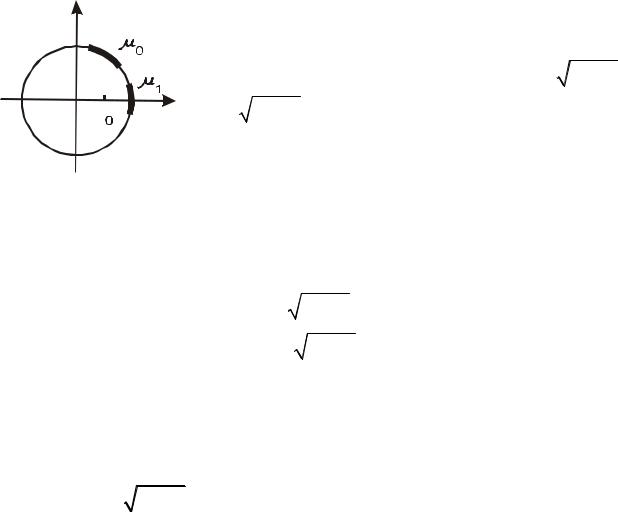
§ 19. Неявная функция. Дифференцирование неявной функции
Неявную (неявно заданную) функцию одной переменной мы уже рассматривали (см. §7 гл.5). Например, уравнение
y |
|
x2 + y2 −1 = 0 |
(окружность |
в R2 ) можно |
|||
|
|
|
|
разрешить относительно x и получить на отрезке |
|||
|
|
|
|||||
|
|
|
|
[−1,1] две явно заданные функции: y = 1− x2 |
и |
||
|
|
|
|||||
|
|
|
|
||||
|
|
|
|||||
|
|
|
|
||||
|
x |
|
x y = − 1− x2 . |
|
x2 + y2 +1 = 0 |
не |
|
|
|
|
|||||
|
|
|
|
Однако другое |
уравнение |
||
определяет ни одной действительной функции. Дело осложняется еще и тем, что уравнение
x2 + y2 −1 = 0 определяет на отрезке [−1,1] не
только две вышеприведенные функции, но и еще бесконечное множество других функций, например, такую:
|
1− x |
2 |
, |
−1 ≤ x < 0, |
|
|
|||
y = |
|
|
|
0 ≤ x ≤1. |
− 1− x2 , |
||||
|
|
|
|
|
Возьмем точку M0 на окружности с некоторой ее окрестностью. Из
рисунка ясно, что эта окрестность взаимно-однозначно проектируется на некоторую окрестность точки x0 оси x . Это означает, что в этой
окрестности уравнение x2 + y2 −1 = 0 определяет единственную явную
функцию y = 1− x2 . Однако, если взять точку M 1 на горизонтальном диаметре окружности, то любая ее окрестность проектируется на ось x
349
