Билеты

1. Упорядоченные пары действительных чисел

Пара чисел является упорядоченной, если указано, какое число из пары является первым и какое - вторым. Комплексными числами называются упорядоченные пары действительных чисел

2. Комплексные числа. Алгебраическая форма комплексного числа.

Комплексные числа являются расширением множества действительных чисел. Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида , где и  — вещественные числа,  — мнимая единица (величина, для которой выполняется равенство: ). Действия над комплексными числами

• Сравнени

еозначает, что и (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

• Сложение

• Вычитание

• Умножение

• Деление

• В частности,

Если комплексное число , то число называется сопряжённым (или комплексно сопряжённым) к (часто обозначается также ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

Алгебраическая форма

Запись комплексного числа в виде , где и , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что ):

3. Полярная система координат. Тригонометрическая форма комплексного числа.

Полярная система координат(в тетрадке) — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ) соответствует расстоянию от точки до начала координат. Угловая координата также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку^.

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число может быть записано в прямоугольной форме так:

где  — мнимая единица, или в полярной (см. формулы преобразования между системами координат выше):

и отсюда:

где  — число Эйлера. Благодаря формуле Эйлера, оба представления эквивалентны^[15] (Следует отметить, что в этой формуле, подобно остальным формулам, содержащим возведения в степень углов, угол задан в радианах)

Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.

Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:

• Умножение:

• Деление:

• Возведение в степень (формула Муавра):

Тригонометрическая форма

Если вещественную и мнимую части комплексного числа выразить через модуль и аргумент (, ), то всякое комплексное число , кроме нуля, можно записать в тригонометрической форме

Пусть задано комплексное число . Как известно, его можно изобразить на комплексной плоскости точкой, абсцисса которой равна действительной части этого числа, то есть , а ордината - мнимой части (рис. 1).

Абсциссу и ординату комплексного числа можно выразить через модуль и аргумент следующим образом:

В данном случае и удовлетворяют соотношениям:

Тогда

Таким образом, для всякого комплексного числа справедливо равенство

которое называется тригонометрической формой комплексного числа .

4. Операции над комплексными числами в тригонометрической форме.

Геометрически комплексные числа складываются по правилу параллелограмма. Но складывать или вычитать два комплексных числа в тригонометрической форме записи крайне затруднительно. Поэтому данные операции в тригонометрической форме записи мы рассматривать не будем.

1.  Умножение.

Правило. При перемножении комплексных чисел в тригонометрической форме записи их модули перемножаются, а аргументы складываются.

2. Деление.

Правило. При делении комплексных чисел в тригонометрической форме записи их модули соответственно делятся, а аргументы вычитаются.

3. Возведение в степень.

Правило. При возведении в n-ую степень комплексного числа в тригонометрической форме записи нужно возвести в n-ую степень модуль, а аргумент умножить на число n.формула Муавра.

4. Извлечение корня.

Правило. Чтобы извлечь корень n-ой степени из комплексного числа в тригонометрической форме записи, нужно извлечь корень n-ой степени из модуля этого комплексного числа, а к аргументу прибавить 2πk и полученную сумму разделить на n

5. Определители и их свойства.

Матрица – прямоугольная таблица, составленная из элементов произвольной природы. Элементы матрицы располагаются в строки и столбцы (иногда их называют колонками). Строки и столбцы часто называют собирательным термином «ряды матрицы». Элементы матрицы часто обозначают двойными индексами – a_ij ; первый индекс i означает номер строки матрицы, в которой стоит элемент a_ij , а второй индекс j означает номер столбца матрицы, в котором стоит a_ij . Матрицы символически обозначают заключёнными в круглые или квадратные скобки, или двойные вертикальные черточки. (Кратко: (a_ij ) или IIa_ij II).

Каждой квадратной матрице, элементами которой являются числа, ставится в соответствие число, называемое определителем матрицы .

Опр. Определитель (детерминант) n-го порядка – алгебраическая сумма n! слагаемых членов из элементов квадратной матрицы (таблицы), которое вычисляется по следующему закону: каждое слагаемое есть произведение n элементов взятых по одному и только по одному из каждой строки и из каждого столбца матрицы. Каждый член определителя берётся со знаком (-1)^t , где t – число инверсий во вторых индексах члена, когда первые индексы члена расположены в натуральном порядке.

Свойства определителя

Определитель обладает рядом свойств:

1) Определитель не изменяется при транспортировании матриц (строк и столбцов).2) Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.

3) Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.

4) Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого

6. Свойства 8 и 9 определителей. Метод Крамера. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.

Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.

СВОЙСТВО 9. Определитель

равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.

Иначе говоря, имеют место следующие равенства:

, ,

, ,

, .

го из трёх определителей одинаковы.

5) Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.

6) Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).

7) Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя.

Правило Крамера: правило решения системы n линейных уравнений. с n неизвестными, определитель которой отличен от нуля, всегда имеет решение. Это решение единственное и определяется таким правилом Крамера: значение каждого из неизвестных , где- определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а_I – определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений.

7. Матрицы и операции над ними.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы^[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Для матрицы определены следующие алгебраические операции:

• сложение матриц, имеющих один и тот же размер;

• умножение матриц подходящего размера (матрицу, имеющую столбцов, можно умножить справа на матрицу, имеющую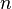строк);

• в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы);

• умножение матрицы на элемент основного кольца или поля (то есть скаляр).

Определение: Если все недиагональные элементы квадратной матрицы равны нулю, то такая матрица называется диагональной (рисунок 2). Обратите внимание: элементы матрицы, расположенные на побочной диагонали, являются недиагональными (кроме элемента, расположенного и на главной диагонали тоже). Определение: Если у диагональной матрицы n–го порядка все диагональ ные элементы равны единице, то такая матрица называется единичной матрицей n–го порядка. (рис.3). То есть у такой матрицы все диагональные элементы равны единице, а недиагональные нулю. Определение: Матрица любого размера называется нулевой, или нуль–ма трицей, если все ее элементы равны нулю (рис. 3).