
- •7.2. БАЗОВАЯ СТРУКТУРА АНАЛИЗАТОРА СПЕКТРА НА ОСНОВЕ ДПФ
- •7.3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ МНОГОКАНАЛЬНОГО АНАЛИЗАТОРА СПЕКТРА НА ОСНОВЕ ДПФ
- •7.4. РОЛЬ ВЕСОВЫХ ФУНКЦИЙ ПРИ ГАРМОНИЧЕСКОМ СПЕКТРАЛЬНОМ АНАЛИЗЕ
- •7.5. ОСНОВНЫЕ ПАРАМЕТРЫ ВЕСОВЫХ ФУНКЦИЙ ПРИ СПЕКТРАЛЬНОМ АНАЛИЗЕ
- •7.6. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ГАРМОНИЧЕСКОГО СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛОВ
- •7.8. КОРРЕЛЯЦИОННЫЕ И СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ СИГНАЛОВ
- •7.10. СТАТИСТИЧЕСКИЕ ОЦЕНКИ КОРРЕЛЯЦИОННЫХ ХАРАКТЕРИСТИК ДИСКРЕТНЫХ СЛУЧАЙНЫХ СИГНАЛОВ
- •7.11. СТАТИСТИЧЕСКИЕ ОЦЕНКИ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ СИГНАЛОВ
- •7.12. КОРРЕЛОГРАММНЫЙ МЕТОД ВЫЧИСЛЕНИЯ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ СИГНАЛОВ
- •7.13. ВЫЧИСЛЕНИЕ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ МЕТОДОМ ПЕРИОДОГРАММ
- •7.14. ВЫЧИСЛЕНИЕ ОЦЕНОК АВТОКОРРЕЛЯЦИИ И ВЗАИМНОЙ КОРРЕЛЯЦИИ С ПОМОЩЬЮ ДПФ
- •7.15. ВЫЧИСЛЕНИЕ ОЦЕНОК АВТОКОРРЕЛЯЦИИ И ВЗАИМНОЙ КОРРЕЛЯЦИИ С ПОМОЩЬЮ ПЕРИОДОГРАММ
- •КОНТРОЛЬНЫЕ ВОПРОСЫ
- •8. АЛГОРИТМЫ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- •8.1. ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ АЛГОРИТМОВ БПФ
- •8.2. АЛГОРИТМ БПФ С ПРОРЕЖИВАНИЕМ ПО ВРЕМЕНИ ПО ОСНОВАНИЮ 2
- •8.4. АЛГОРИТМ БПФ ПО ОСНОВАНИЮ 2 С ПРОРЕЖИВАНИЕМ ПО ЧАСТОТЕ И ГРАФ-СХЕМА ЕГО ПРОГРАММНОЙ РЕАЛИЗАЦИИ
- •8.5. МАСШТАБИРОВАНИЕ И ОЦЕНКА ТОЧНОСТИ ПРИ ВЫЧИСЛЕНИИ БПФ
- •8.6. ДОПОЛНИТЕЛЬНЫЕ ВОЗМОЖНОСТИ АЛГОРИТМОВ БПФ
- •КОНТРОЛЬНЫЕ ВОПРОСЫ
- •9. ПЕРЕНОС И ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ДИСКРЕТНЫХ СИГНАЛОВ
- •9.1. ЗАДАЧИ ПРЕОБРАЗОВАНИЯ СПЕКТРОВ ДИСКРЕТНЫХ СИГНАЛОВ В СИСТЕМАХ ЦОС
- •9.3. ПЕРЕНОС СПЕКТРОВ И КВАДРАТУРНАЯ ОБРАБОТКА УЗКОПОЛОСНЫХ РАДИОСИГНАЛОВ
- •9.4. ФОРМИРОВАНИЕ ОДНОПОЛОСНЫХ ДИСКРЕТНЫХ СИГНАЛОВ
- •9.4.1. ФИЛЬТРОВОЙ СПОСОБ ФОРМИРОВАНИЯ ОДНОПОЛОСНЫХ ДИСКРЕТНЫХ СИГНАЛОВ
- •9.4.2. ФОРМИРОВАНИЕ ОДНОПОЛОСНОГО ДИСКРЕТНОГО СИГНАЛА С ПОМОЩЬЮ ПРЕОБРАЗОВАТЕЛЯ ГИЛЬБЕРТА
- •КОНТРОЛЬНЫЕ ВОПРОСЫ
- •КОНТРОЛЬНЫЕ ВОПРОСЫ
- •12.2. АППАРАТНАЯ РЕАЛИЗАЦИЯ ЦОС
- •12.2.1. ЗАДАЧИ И СПОСОБЫ АППАРАТНОЙ РЕАЛИЗАЦИИ ЦОС
- •12.2.4. ЦИФРОВЫЕ ФИЛЬТРЫ С РАСПАРАЛЛЕЛИВАНИЕМ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
- •12.2.6. ЦИФРОВЫЕ ФИЛЬТРЫ С ВРЕМЕННЫМ РАЗДЕЛЕНИЕМ СИГНАЛОВ
- •12.3.2. СИНХРОНИЗАЦИЯ И АЛГОРИТМЫ РАБОТЫ МИКРОПРОЦЕССОРНЫХ СИСТЕМ ЦОС
- •12.3.3. СПОСОБЫ И ЗАДАЧИ РАЗРАБОТКИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ МИКРОПРОЦЕССОРНЫХ СИСТЕМ ЦОС
- •12.4. ОБЩАЯ ХАРАКТЕРИСТИКА ЦИФРОВЫХ СИГНАЛЬНЫХ ПРОЦЕССОРОВ
- •КОНТРОЛЬНЫЕ ВОПРОСЫ
- •ЛИТЕРАТУРА
17
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X(jω 0 , n) |
|||
x(n) |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∑ |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
z− 1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
z− N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
-jω |
nT |
д |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(n |
– |
N) |
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X(jω 1 , n) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
z− 1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e-jω 1nTд |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X(jω N –1 , n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
z− 1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e-jω |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N − 1nTд |
|
|
|
|||||||||||||
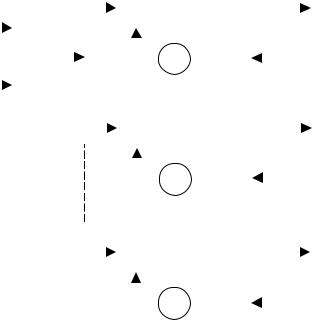
Рис. 7.5. Структура анализатора спектра на основе гребенки фильтров Такой анализатор спектра с прямоугольной весовой функцией требует
N комплексных операций умножения на один отсчет сигнала. Число каналов его определяется требуемой полосой анализа сигнала. Каждый канал анализатора спектра описывается следующим рекуррентным уравнением:
X ( jω k , n ) = e− jω k nTд X ( jω k , n − 1) + x( n ) − x( n − N ).
7.8. КОРРЕЛЯЦИОННЫЕ И СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ СИГНАЛОВ
Дискретные случайные сигналы, как и аналоговые, характеризуются законом распределения, средним значением, средним квадратом или дисперсией, автокорреляцией или автоковариацией, взаимной корреляцией (кросс-корреляцией) или взаимной ковариацией, спектральной плотностью мощности и взаимной спектральной плотностью мощности. Для рассматриваемых далее случайных процессов стационарных в широком смысле и эргодичных полагается, что их среднее значение является
постоянным, не зависящим от времени nTд, т. е. от номера выборки n, а автокорреляция и взаимная корреляция зависят только от разности моментов времени mTд = n2Tд − n1Tд , т. е. от значения дискретной задержки m. Они определяются как математические ожидания Ε { } (средние по ансамблю) или как средние по времени (по одной реализации) соответствующих дискретных функций [2].
Среднее значение дискретного сигнала x(n):
18
|
|
|
1 |
|
N |
||
x = Ε {x( n )} = |
lim |
|
|
|
|
∑ |
x( n ). |
N → |
∞ 2N + |
|
|||||
|
|
1n = − N |
|||||
Автокорреляционная функция (АКФ) дискретного сигнала x(n):
r |
( m ) = Ε {x( n + |
m )x* ( n )} = |
lim |
|
1 |
|
N x( n + |
m )x* ( n ). |
|
|
|||||||
xx |
|
|
|
N → ∞ |
2N + 1n =∑− N |
|
||
Взаимная корреляционная функция (ВКФ) двух дискретных |
||||||||
сигналов x(n) и y(n): |
|
|
|
|
|
N x( n + |
|
|
r |
( m ) = Ε {x( n + |
m )y* ( n )} = |
lim |
|
1 |
|
m )y* ( n ), |
|
|
|
|
||||||
xy |
|
|
|
N → ∞ |
2N + 1n =∑− N |
|
||
где символ * означает операцию комплексного сопряжения, обобщающую данные статистические характеристики на случай комплексных дискретных сигналов. По максимуму ВКФ находят относительное время задержки обрабатываемых сигналов [3, 5].
АКФ и ВКФ центрированных случайных сигналов [x(n) – x ] и
сигналов с нулевым средним значением называют автоковариационной
сxx(m) и взаимной ковариационной сxу(m) функциями:
cxx ( m ) = Ε {[x( n + m ) − x][x* ( n )− x]}; cxy ( m ) = Ε {[x( n + m ) − x][y* ( n ) − y*]}.
При этом cxx ( m ) = rxx ( m ) − |
| x |2 ; cxy ( m ) = |
rxy ( m ) − x y * . |
|
|
|
||||||||||
АКФ rxx(m) при m = 0 |
соответствует среднему квадрату случайного |
||||||||||||||
сигнала: |
|
|
|
|
|
|
|
|
|
N x( n )x* ( n ), |
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
x2 |
= r |
( 0 ) = Ε {x( n )x* ( n )} = |
lim |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
xx |
|
|
|
|
|
N→ ∞ |
2N + 1n =∑− N |
|
|
|
|||
а автоковариационная функция с |
(m) |
– дисперсии сигнала: с (0) = D |
x |
= σ |
2. |
||||||||||
|
|
|
|
|
xx |
|
|
|
− | x |2 |
|
xx |
|
x |
||
Они связаны |
соотношением: |
Dx = |
|
x2 |
и определяют среднюю |
||||||||||
мощность случайного сигнала. Средний квадрат и дисперсия являются максимальными значениями соответственно автокорреляционной и автоковариационной функций. В дальнейшем данные термины (средний квадрат – дисперсия), (автокорреляция – автоковариация) используются как синонимы.
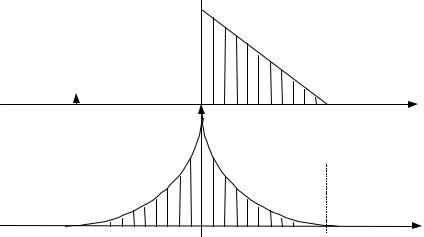
АКФ и ВКФ обладают свойствами симметрии вида: rxx(− m) = rxx*(m); rxy(− m) = rxy*(m). На рис. 7.6 показан примерный вид АКФ треугольной дискретной последовательности конечной длины N1.
19
x(n)N1 
n
rx(m) |
0 1 2 |
. . . |
N1 − 1 |
m
− (N1 − 1) |
0 |
N1 − 1 |
0 |
N1 |
2N1 − 1 |
Рис. 7.6. Пример представления автокорреляционной функции дискретного сигнала
Спектральную плотность мощности (СПМ) случайного процесса в соответствии с теоремой Винера− Хинчина [1–3] определяют преобразованием Фурье АКФ (последовательности rxx(m)):
∞ |
|
− j2π |
f mTд |
|
|
Pxx ( f ) = Tд ∑ |
rxx ( m )e |
(7.8) |
|||
|
|
||||
m = |
− ∞ |
|
|
|
для значений частоты f, заключенных в основной полосе частот (0± fД/2). СПМ показывает, как мощность случайного процесса распределена по частоте. Так как rxx(− m) = rxx*(m), то СПМ является строго действительной положительной функцией. Если АКФ – действительна,
то rxx(− m) = rxx(m) и выражение для СПМ приводится к виду:
Pxx ( f ) = 2Tд ∑∞ |
rxx ( m )cos( 2π f mTд ) . |
m = |
− ∞ |
При этом Pxx(f) обладает свойством четной симметрии: Pxx(f) = Pxx(− f).
АКФ случайного сигнала может быть определена по его известной СПМ с помощью обратного преобразования Фурье:
|
f д / 2 |
|
rxx ( m ) = |
∫ Pxx ( f )e j2π f mTд df . |
(7.9) |
− f д / 2
20
|
|
f д / 2 |
|
При m = 0 |
rxx ( 0 ) = |
∫ Pxx ( f )df |
соответствует средней мощности |
|
− |
f д / 2 |
|
сигнала или его дисперсии.
Аналогичным образом вводится определение взаимной спектральной плотности мощности (ВСПМ) двух стационарных случайных сигналов x(n) и y(n) как преобразование Фурье их ВКФ [1, 2, 3]:
Pxy ( jf ) = Tд ∑∞ |
rxy ( m )e− j2π f mTд . |
(7.10) |
m = |
− ∞ |
|
Даже для действительных последовательностей x(n) и y(n) вследствие несимметрии их ВКФ (rxy(− m) ≠ rxy(m)) ВСПМ является в общем случае комплексной. В то же время она обладает свойством Pxy(jf) = Pyx*(jf).
Простейшим, но важным является дискретный случайный процесс типа
белый шум ν (n). Его АКФ r ( m ) = |
σ |
ν |
|
2u |
0 |
( m ), где u |
(m) = |
1 при m =0 и |
|||||||||||||||||||||||
u0(m) = 0 при m ≠ |
|
|
|
|
νν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
0 – единичный импульс. СПМ белого шума |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
P ( f ) = T |
|
σ |
ν |
2 |
= σ |
|
ν |
2 |
/ f |
д |
= |
N |
o |
. |
|
|
|
|
|
|
|||||||
|
|
|
|
νν |
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Условию эргодичности процесса отвечает следующая эквивалентная |
|||||||||||||||||||||||||||||||
(7.8) форма определения СПМ [2]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
N |
|
|
|
|
− |
j2π f nT |
2 |
|
|
|
|||||
|
( f ) = |
|
|
Ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||||||||
P |
lim |
|
|
|
|
|
|
|
|
| T |
|
|
∑ |
x( n ) e |
|
|
|
|
д | |
|
|
|
(7.11) |
||||||||
N → ∞ |
( 2N |
+ |
1)T |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
xx |
|
|
|
|
д |
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = − |
N |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
= lim N → ∞ |
Ε |
|
X ( jf )X * ( jf |
) |
= |
|
lim N |
→ ∞ |
Ε |
|
|
|
| X ( jf ) |2 . |
||||||||||||||||||
( 2N + 1)T |
|
( 2N + 1)T |
|
||||||||||||||||||||||||||||
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
||
Она соответствует математическому ожиданию или статистически усредненному квадрату модуля преобразования Фурье дискретной последовательности x(n), поделенному на ее длину, стремящуюся в пределе к бесконечности. Такое определение включает усреднение и по времени и по ансамблю. Следует отметить, что исключение операции Ε { } – усреднения по ансамблю приводит к резкому возрастанию дисперсии такого рода оценки СПМ [2, 12].
В эквивалентном выражении для ВСПМ квадрат модуля |X(jf)|2 в
(7.11) заменяется на произведение X(jf)Y*(jf).
21
7.9.ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ СИГНАЛОВ
ВЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМАХ
Если x(n) – дискретный случайный сигнал с нулевым средним значением, то сигнал на выходе линейной дискретной системы определяется
дискретной временной сверткой: y( n ) = ∑∞ |
h( l )x( n − l ) = x( n ) h( n ), где − |
l − |
∞ |
символ свертки. Статистические характеристики случайного выходного сигнала y(n) связаны со статистическими характеристиками входного сигнала и импульсной характеристики дискретной системы соотношениями [2]:
ryx ( m ) = rxx ( m ) h( m ); rxy ( m ) = rxx ( m ) h* ( − m ); |
|
|
ryy ( m ) = rxy ( m ) h( m )= rxx ( m ) [h* ( − m ) h( m )] = |
(7.12) |
|
= rxx ( m ) [ ∑∞ h( l + m )h* ( l )] . |
|
|
l = −∞ |
|
|
В случае вещественной импульсной характеристики h(n) |
|
|
rxy ( m ) = rxx( m ) h( − m ); ryy ( m ) = rxx( m ) [ ∑∞ |
h( l + m )h( l )] . |
|
l = |
−∞ |
|
Cумма в правой части последнего выражения имеет смысл АКФ импульсной характеристики системы.
Соотношения (7.12) представляются также на комплексной Z- |
|||
плоскости с помощью Z-преобразований АКФ, ВКФ, импульсной |
|||
характеристики |
|
|
Pxx ( z ) = Z{rxx ( m }) , |
Pxy ( z ) = Z{rxy ( m )}, Pyy ( z ) = Z{ryy ( m )}, H( z ) = Z{h( n }) |
и теоремы о |
||
свертке: |
|
|
|
Pyx( z ) = |
Pxx ( z )H( z ); |
Pyx( z ) = Pxx( z )H * (1/ z*); |
|
Pyy ( z ) = |
Pxy ( z )H( z ) = |
Pxx( z )H( z )H * (1/ z*) , |
(7.13) |
|
|||
где H*(1/z*) =Z{h*(− m)}. Для действительной импульсной характеристики
H*(1/z*) = H(1/z).
Заменяя в выражениях (7.13) z |
на |
ej2π fTд |
можно |
перейти к |
|
соответствующим соотношениям |
для |
СПМ |
и ВСПМ. В |
частности, |
|
Pyy ( f ) = Pxx ( f ) | H( jf ) |2 , где |
|H(jf)|2 |
– квадрат |
модуля |
частотной |
|
характеристики дискретной системы. Вычисляя СПМ и ВСПМ входной и выходной последовательностей дискретной системы, можно определить ее
частотную характеристику, т. е. решить задачу идентификации объектов.
