ГЛАВА 6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
6.2.Классический метод расчета переходных процессов
6.2.3.Разряд конденсатора на резистор
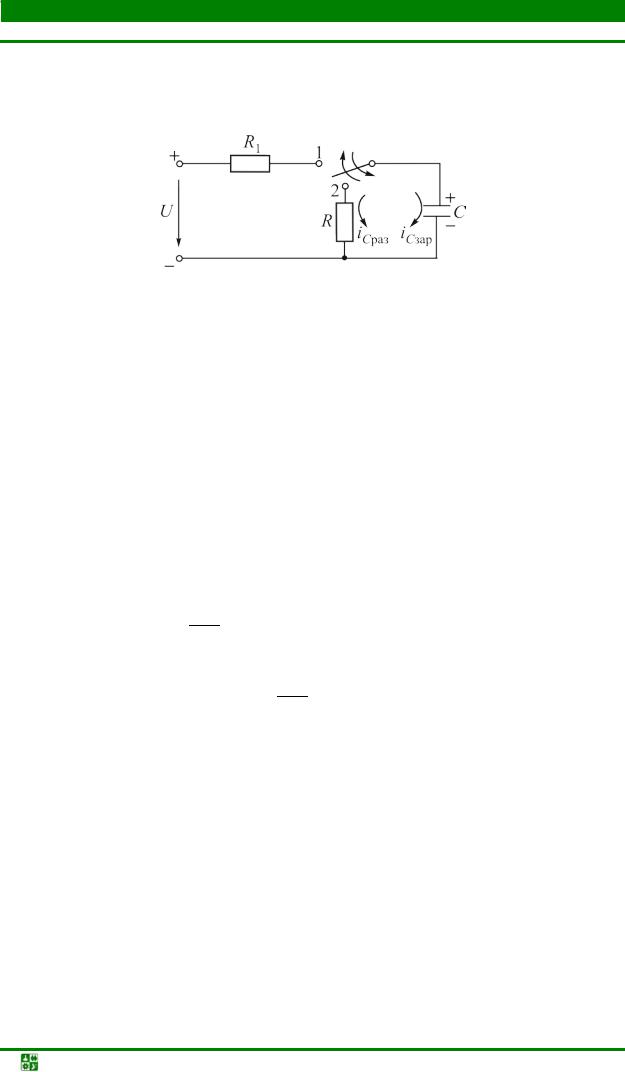
Схема замещения рассматриваемой цепи представлена на рис. 6.7.
Рис. 6.7
В положении ключа 1 происходит уже рассмотренный процесс заряда конденсатора до напряжения источника U с постоянной времени τçàð = R1C.
Ток заряда конденсатора направлен от положительного зажима источника к отрицательному.
При положении ключа 2 конденсатор разряжается на резистор сопротивлением R. Ток iÑ ðàç направлен от положительно заряженной обкладки
конденсатора.
Составим уравнение электрического состояния цепи разряда конденсатора:
RiÑ + uÑ = 0.
Подставив iÑ = C dudtÑ , получим
RC dudtÑ + uÑ = 0 .
Это уравнение однородное, поэтому решение содержит только одно слагаемое uÑñâ . Принужденная составляющая uÑ ï ð = 0, что очевидно, так как
конденсатор разряжается.
Свободная составляющая меняется по закону экспоненты:
uÑñâ = Àåpt .
Характеристическое уравнение RСp +1 = 0 . Отсюда
Теоретические основы электротехники. Учеб. пособие |
-160- |
|
ГЛАВА 6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ |
|
||||||||
|
6.2. Классический метод расчета переходных процессов |
|
||||||||
|
p = − |
1 = − |
1 . |
|
|
|
|
|
|
|
|
|
RC |
τðàç |
|
|
|
|
|
|
|
Определим постоянную интегрирования А из начальных условий с ис- |
||||||||||
пользованием законов коммутации: |
|
|
|
|
|
|
|
|
|
|
|
uÑ (0+) = uÑ ñâ (0+) . |
|
|
|
|
|
|
|||
Напряжение uÑ (0+) = uÑ (0−) =U ; uÑ ñâ (0+) = A. |
|
|
|
|
|
|
||||
Тогда U = A. |
|
|
|
|
|
|
|
|
|
|
Напряжение на конденсаторе при его разряде меняется по закону |
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
u |
=Ue−RC t . |
|
|
|
|
|
|
|
|
|
Ñ |
|
|
|
|
|
|
|
|
|
Ток разряда конденсатора i |
u |
|
U |
e |
− |
1 |
t |
. Токи заряда и разряда |
||
= − Ñ = − |
|
|
RC |
|
||||||
|
Ñ |
R |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
конденсатора направлены противоположно. |
|
|
|
|
|
|
|
|||
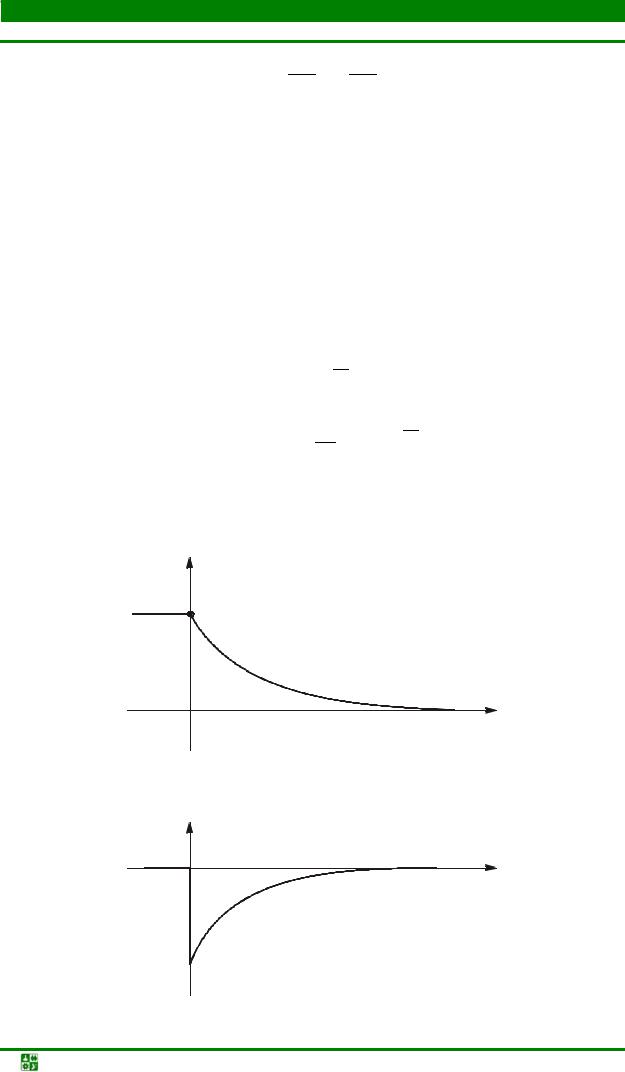
Графики изменения uÑ и iÑ приведены на рис. 6.8 и рис. 6.9. |
|
|||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
Рис. 6.8 |
|
|
|
|
|
|
|
|
|
iC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
–U |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.9 |
|
|
|
|
|
|
|
|
|
Теоретические основы электротехники. Учеб. пособие |
-161- |
||||||||
ГЛАВА 6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ |
|
6.2. Классический метод расчета переходных процессов |
|
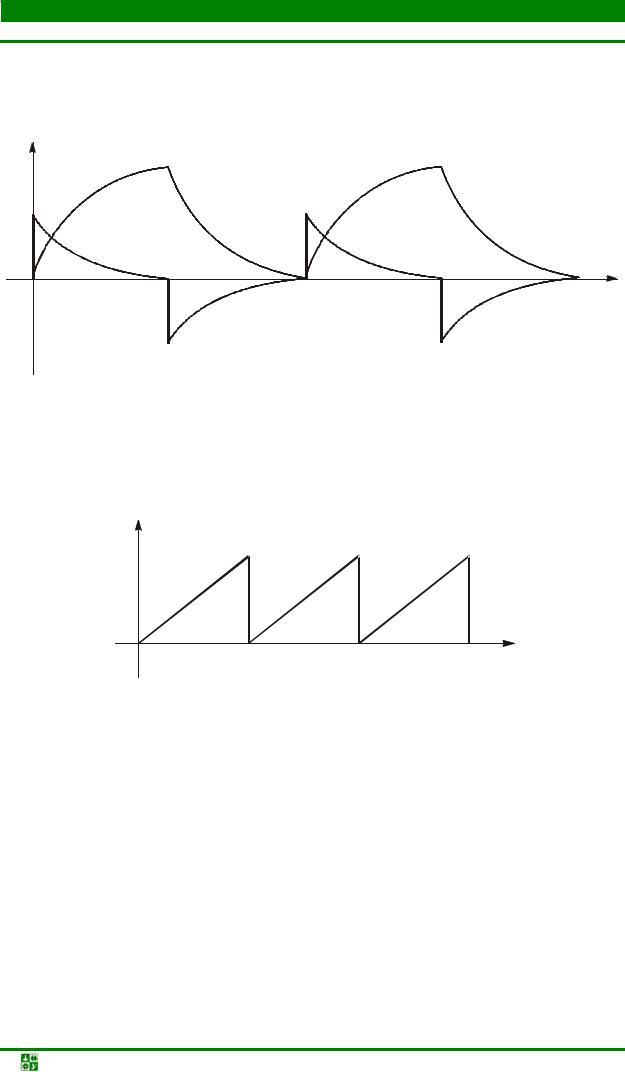
При периодическом переключении рубильника из положения 1 в по- |
|
ложение 2 и обратно графики изменения uÑ и iÑ будут иметь вид, представ- |
|
ленный на рис. 6.10. |
|
uC |
|
iC |
|
|
t |
Рис. 6.10 |
|
Если путем подбора параметров добиться, чтобы τçàð |
стало много |
больше τðàç , то график изменения uÑ будет иметь вид, представленный на |
|
рис. 6.11. |
|
C |
|
t |
|
Рис. 6.11 |
|
Вэтом случае схема на рис. 6.7 будет являться простейшим генератором пилообразного напряжения (релаксационным генератором), который используют в качестве генератора развертки в телевизорах и осциллографах.
ВМосковском политехническом музее демонстрируют телевизионный приемник с механической разверткой. Механизм механической развертки выставлен на обозрение отдельно. Он представляет собой отполированный до зеркального блеска винт с вертикальной осью, приводимый во вращение электродвигателем. Высота этого телевизора около полутора метров, круглый экран размером немного превышает пятирублевую монету.
Именно использование релаксационного генератора, в основу принципа действия которого положены переходные процессы, сделало возможным повсеместное применение телевизионных приемников.
Теоретические основы электротехники. Учеб. пособие |
-162- |
ГЛАВА 6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
6.2. Классический метод расчета переходных процессов
6.2.4. Подключение реальной катушки к источнику постоянного напряжения
Схема замещения анализируемой цепи приведена на рис. 6.12.
Рис. 6.12
Уравнение электрического состояния в дифференциальной форме:
uL + uR =U .
После подстановки uL и uR , выраженных по закону Ома, получим уравнение с одной переменной:
L didtL + RiL =U .
Решение этого уравнения является суммой двух слагаемых:
iL = iLï ð +iLñâ .
Найдем iLï ð в схеме при t = ∞. Индуктивный элемент не оказывает со-
противления постоянному току, вместо него будет закоротка. Тогда iLï ð = UR . Вычислим iLñâ по закону экспоненты:
|
|
iLñâ = Àåpt . |
1. Составим характеристическое уравнение для определения |
||
p : Lp + R = 0. |
|
|
Отсюда p = − R . |
|
|
L |
1 |
= L . |
Постоянная времени τ = |
||
|
p |
R |
Так как [L] = Гн = с Ом, то [τ] = с.
2. Определим постоянную интегрирования А из начальных условий с использованием законов коммутации.
В начальный момент времени
Теоретические основы электротехники. Учеб. пособие |
-163- |
ГЛАВА 6. ПЕРЕХОДНЫЕ ПРОЦЕССЫ |
|
|
|
|
||||||||||||||
6.2. Классический метод расчета переходных процессов |
|
|
||||||||||||||||
iL (0+) = iLï ð (0+) +iLñâ (0+) . |
|
|
|
|
|
|
|
|
||||||||||
По первому закону коммутации iL (0+) = iL (0−) . До коммутации схема не бы- |
||||||||||||||||||
ла подключена к источнику энергии, поэтому iL (0−) = 0. |
|
|
|
|
||||||||||||||
Принужденная составляющая iLï ð = U |
|
– постоянная величина. Свобод- |
||||||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ная составляющая в начальный момент iLñâ (0+) = À. |
|
|
|
|
|
|
|
|
||||||||||
После подстановки получим: 0 = U |
+ A . Отсюда |
A = −U . |
|
|
||||||||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
Тогда закон изменения тока iL = |
U |
− |
U |
e |
−R t |
. |
|
|
|
|
|
|
|
|
||||
|
R |
R |
L |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
Закон изменения напряжения uR |
= RiL |
=U −Ue− L t . |
|
|
|
|
|
|||||||||||
Закон изменения напряжения uL |
= L |
|
di |
L = L |
U |
|
R |
e |
−R t |
=Ue |
−R t |
. |
||||||
|
|
R |
L |
L |
|
L |
||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
R |
|
|
|
R |
|
|
|
|
|
В любой момент времени uR + uL |
=U −Ue− L t +Ue− L t |
=U . |
|
|
||||||||||||||
Проиллюстрируем полученные законы изменения электрических вели- |
||||||||||||||||||
чин графиками. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
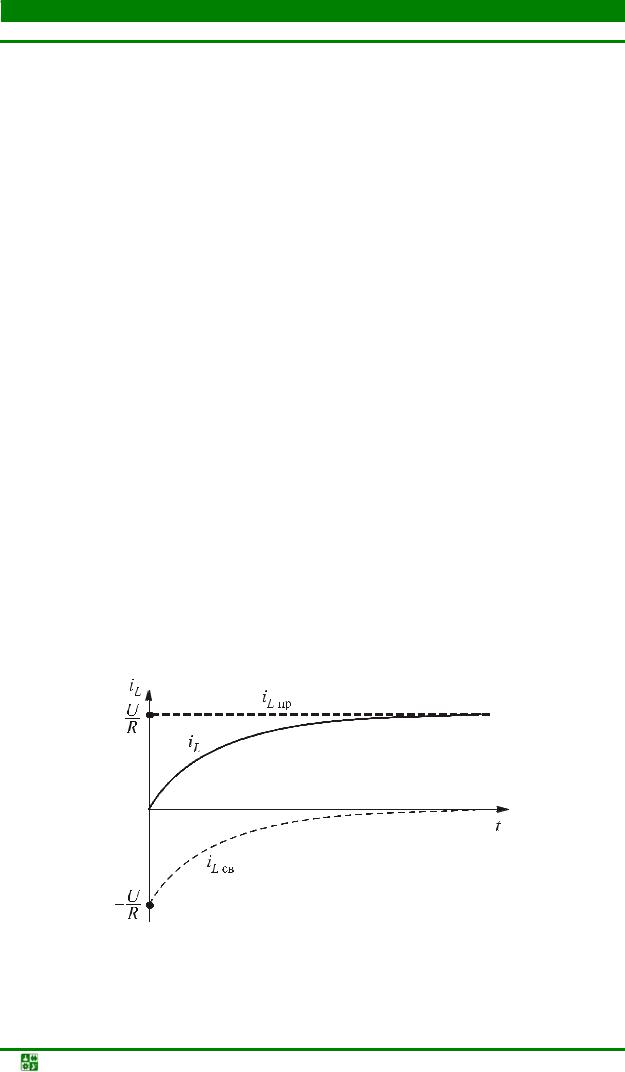
График тока iL (рис. 6.13) получаем как сумму графиков iLï ð |
и iLñâ . Со- |
|||||||||||||||||
ставляющая тока iLï ð = U = const . Свободная составляющая меняется по за- |
||||||||||||||||||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кону экспоненты и стремится к нулю. В начальный момент iL (0+) = −U . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ñâ |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.13 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Из графика видно, что ток в индуктивной катушке меняется плавно и |
||||||||||||||||||
стремится к принужденной составляющей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теоретические основы электротехники. Учеб. пособие |
-164- |