ГЛАВА 3 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
3.14.Электрическиецеписвзаимнойиндуктивностью
3.14.1.Основные понятия и определения
При всяком изменении магнитного потока, пронизывающего какойлибо контур, в последнем наводится ЭДС.
Если магнитный поток создан током этого же контура, то говорят о явлении самоиндукции, ЭДС самоиндукции eL и индуктивности L.
Если магнитный поток создан током другого контура, то говорят о явлении взаимоиндукции, ЭДС взаимоиндукции eM и взаимной индуктивности М.
Рассмотрим две индуктивные катушки, имеющие магнитную связь (рис. 3.52). Зажимы второй катушки разомкнуты.
Если первую индуктивную катушку подключить к источнику напряжения u1, в ней появится т ок i1 , который создает магнитный поток Ф11, часть
которого Ф12 пронизывает витки второй катушки. Часть магнитного потока замыкается по воздуху (магнитный поток рассеяния Ф1S ).
i1 |
R1 |
Ф12 |
u1 |
Ф1S |
L1 |
|
W1 |
|||
|
|
|
|
R2 |
|||
|
L2 |
|
|
|
u2 |
|
|
|
|
||
|
|
|
|
||
|
W2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.52
Потокосцепление самоиндукции ψ11 =W1Ф11 наводит в первой катушке
ЭДС самоиндукции e = − |
dψФ |
= −W |
dd |
11 |
= −L |
i |
|
11 |
|
1 |
. |
||||
|
|
|
|||||
L |
dt |
1 |
dt |
1 |
dt |
||
1 |
|
|
|||||
|
|
|
|
|
|
|
|
Потокосцепление взаимоиндукции ψ12 =W2Ф12 наводит во второй ка-
тушке ЭДС взаимоиндукции e = − |
dψФ |
= −W |
d |
12 |
. |
12 |
|
||||
|
|
||||
М2 |
dt |
2 |
|
dt |
|
|
|
|
|||
Коэффициент, характеризующий способность тока создавать магнитный поток в другом контуре, называют взаимной индуктивностью М.
Взаимная индуктивность
Ì 12 |
= |
dψ12 |
. |
|
|||
|
|
di1 |
|
Тогда eM2 = −M12 ddit1 .
Теоретические основы электротехники. Учеб. пособие |
-79- |
ГЛАВА 3. ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
3.14. Электрические цепи с взаимной индуктивностью
Уравнения электрического состояния схемы замещения цепи нарис. 3.52:
u1 = R1i1 + L1 ddit1 ; u2 = −eM2 = M12 ddit1 .
Если зажимы второй катушки замкнуть, в ней появится токi2 . Все рассмотренное ранее наблюдается и в этом случае. Ток i2 создает магнитный
поток Ф22 = Ф21 + Ф2S .
Потокосцепление самоиндукции ψ22 =W2Ô22 наводит во второй катушке ЭДС самоиндукции
e = − |
dψФ |
= −W |
dd |
22 |
= −L |
i |
|
22 |
|
2 |
. |
||||
|
|
|
|||||
L |
dt |
2 |
dt |
2 |
dt |
||
2 |
|
|
|||||
|
|
|
|
|
|
|
|
Потокосцепление взаимоиндукции ψ21 =W1Ô21 наводит в первой катушке ЭДС взаимоиндукции
e М= − |
dψФ |
= −W |
d |
d |
|
|
i |
|
21 |
|
21 |
= − |
21 |
2 |
. |
||
|
|
|||||||
М1 |
dt |
1 |
|
dt |
|
dt |
||
|
|
|
|
|
||||
По принципу взаимности для линейных цепей М12 = М21 = М .
Степень индуктивной связи характеризуют коэффициентом связи k, под которым понимают отношение:
k = |
|
M |
|
= |
|
M ω |
= |
|
|
X M |
|
|
|
, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L |
L |
|
|
L |
ω L ω |
|
X |
L |
|
X |
|
||||||
|
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
L |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
где X M = M ω – сопротивление взаимной индукции.
Для решения вопроса о знаках прибегают к специальной разметке зажимов индуктивно связанных катушек. Два зажима двух индуктивно связанных элементов называют одноименными, если при одинаковых направлениях токов относительно них магнитные потоки самоиндукции и взаимоиндукции складываются. Одноименные зажимы обозначают точками.
Одноименные зажимы двух индуктивно связанных элементов обладают особенностью: при увеличении тока, направленного к зажиму одного элемента, возрастает потенциал на одноименном зажиме другого элемента. Поэтому на практике одноименные зажимы определяют следующим образом (рис. 3.53):
Теоретические основы электротехники. Учеб. пособие |
-80- |
ГЛАВА 3. ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
3.14. Электрические цепи с взаимной индуктивностью
R1 |
R2 |
+ |
|
|
|
|
|
+ |
E |
L1 |
|
L2 |
V |
|
|
_ |
|
|
|
|
|
_ |
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
RV 
∞
Рис. 3.53
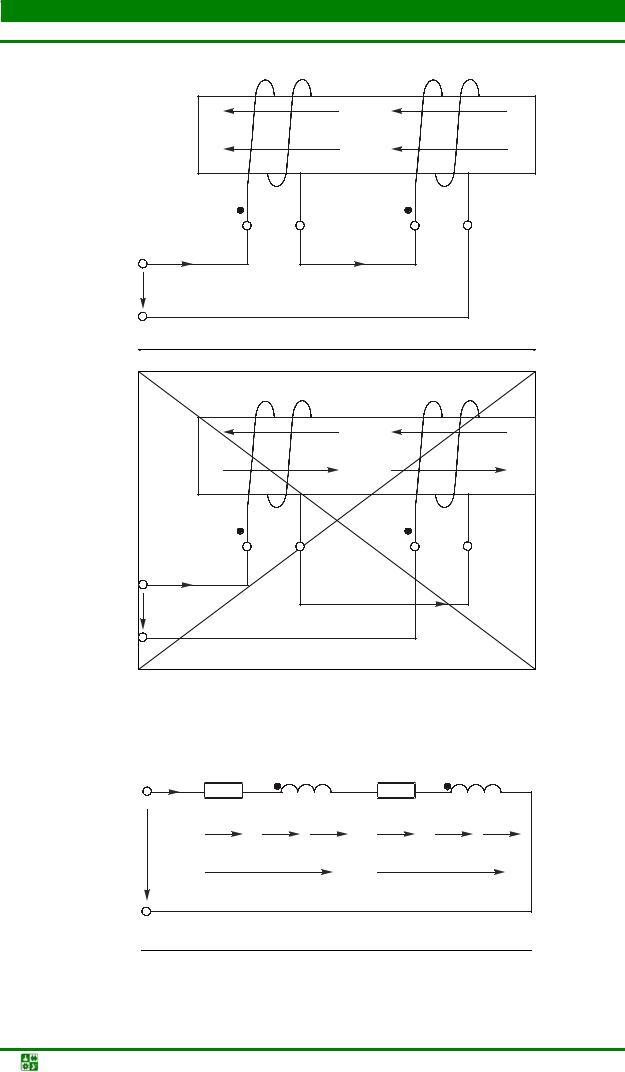
1) одну индуктивную катушку подключают к источнику постоянного напряжения;
2) к другой индуктивной катушке подключают вольтметр для измерения постоянного напряжения;
3) концы индуктивных катушек, подключенные к положительному полюсу источника и к положительному зажиму вольтметра, будут одноименными, если при замыкании ключа стрелка прибора отклонится в сторону положительных значений измеряемого напряжения.
3.14.2. Анализ цепи с последовательным соединением индуктивно связанных катушек
Возможны два случая включения: согласное и встречное.
При согласном включении магнитный поток самоиндукции совпадает по направлению с магнитным потоком взаимной индукции другой катушки. Это будет при одинаковых направлениях токов относительно одноименных зажимов (рис. 3.54). Направление магнитного потока определяют по правилу буравчика или правой руки: если охватить рукой катушку (пальцы направлены по току), то большой палец покажет направление магнитного потока.
При встречном включении магнитные потоки самоиндукции и взаимной индукции направлены противоположно. Это будет, если токи ориентированы относительно одноименных зажимов по-разному (рис. 3.55).
Теоретические основы электротехники. Учеб. пособие |
-81- |
ГЛАВА 3. ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА |
|||
3.14. Электрические цепи с взаимной индуктивностью |
|||
|
W1 |
|
W2 |
|
ψ11 |
|
ψ12 |
|
ψ21 |
|
ψ22 |
a |
b |
c |
d |
i |
i |
|
|
u |
|
|
|
|
Рис. 3.54 |
|
|
|
W1 |
|
W2 |
|
ψ11 |
|
ψ12 |
|
ψ21 |
|
ψ22 |
a |
b |
c |
d |
i |
|
i |
|
u |
|
|
|
|
|
|
|
|
Рис. 3.55 |
|
|
1. Согласное включение. |
|
|
|
Схема замещения цепи представлена на рис. 3.56. |
|
||
i |
R1 |
L 1 |
R2 |
L 2 |
|
|
|
uR1 |
u L1 |
uM |
uR2 |
uL2 |
uM |
u |
|
u1 |
|
|
u2 |
|
|
|
|
Рис. 3.56 |
|
|
|
Входное напряжение складывается из напряжений на двух индуктив-
Теоретические основы электротехники. Учеб. пособие |
-82- |
ГЛАВА 3. ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
3.14. Электрические цепи с взаимной индуктивностью
ных катушках. Напряжения собственной индуктивности uL и взаимной индуктивности uM имеют одинаковые знаки.
Уравнение электрического состояния в дифференциальной форме:
u = u1 +u2 = R1i + L1 ddti + M ddti + R2i + L2 ddti + M ddti .
Для комплексных значений
U =U |
1 |
+U |
2 |
= R I + jX |
L |
I + jX |
M |
I + R |
2 |
I + jX |
L |
I + jX |
M |
I = |
||
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
= (R1 |
+ R2 )+ j(X L1 |
+ X L2 |
+ 2XM ) I = Z согл I . |
|
|
||||||||||
Комплексное сопротивление
Z согл = Rсогл + jXсогл ,
где Rсогл = R1 + R2 , Xсогл = X L1 + X L2 + 2XM .
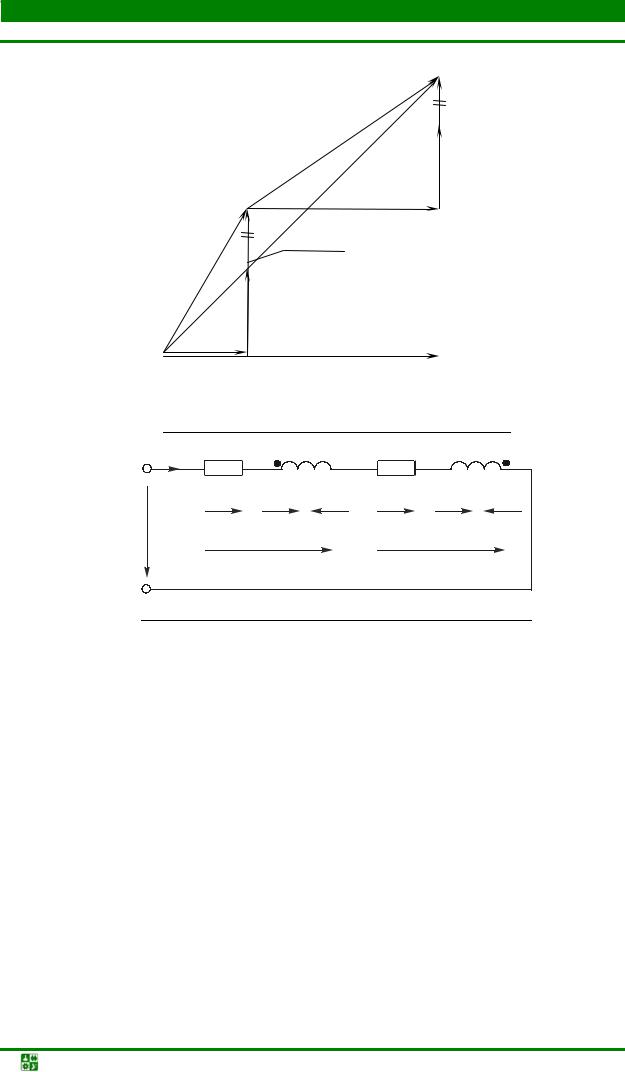
Векторная диаграмма приведена на рис. 3.57.
2. Встречное включение.
Схема замещения цепи представлена на рис. 3.58.
Напряжения собственной индуктивности uL и взаимной индуктивности uM направлены противоположно. Уравнение электрического состояния в дифференциальной форме:
Теоретические основы электротехники. Учеб. пособие |
-83- |
ГЛАВА 3. ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА |
|||||||||||
3.14. Электрические цепи с взаимной индуктивностью |
|||||||||||
|
|
|
|
|
|
|
|
|
|
jX M I |
|
|
|
|
|
|
U2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
jX L I |
|
|
|
|
|
|
|
|
U |
R2 I |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
||||
U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jX M I |
|
|
|
|
|
|
|
|
|
|
|
jX L I |
|
|
|
|
|
|
|
R1I |
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
Рис. 3.57 |
|
|
|
|
|
|
|
i |
R1 |
|
L 1 |
|
|
R2 |
|
|
L 2 |
||
|
uR1 |
|
u L1 |
uM |
|
uR2 |
uL2 |
uM |
|||
u |
|
|
u1 |
|
|
|
u2 |
|
|
|
|
|
|
|
|
Рис. 3.58 |
|
|
|
|
|
||
u = u +u |
|
= R i + L di |
− M di |
+ R |
i + L |
di |
− M di . |
||||
1 |
2 |
|
1 |
1 dt |
|
dt |
2 |
|
|
2 dt |
dt |
Для комплексных значений |
|
|
|
|
|
|
|
||||
U =U |
1 |
+U |
2 |
= R I + jX |
L |
I − jX |
M |
I + R |
2 |
+ jX |
L |
I − jX |
M |
I = |
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
= (R1 |
+ R2 )+ j(X L1 + X L2 |
− 2XM ) I = Z встрI . |
|
|
||||||||||
Комплексное сопротивление
Z встр = Rвстр + jXвстр ,
где Rвстр = Rсогл = R1 + R2 , Xвстр = X L1 + X L2 − 2XM .
Величину сопротивления взаимной индуктивности X M и взаимной
Теоретические основы электротехники. Учеб. пособие |
-84- |