Экзамен по ЧМРТЗ

Тема 14. Интерполяция, экстраполяция, линейная интерполяция.

Интерполяция зависимостей используется для решения тех или иных задачю Функции могут задаваться как аналитические, так и табличные. При использовании таблиц значения функций известны при дискретных значениях аргумента. Часто возникает проблема иметь более подробные таблицы.

Путем приближѐнной замены функции f(x) более простой φ(x), которую можно вычислить при любом значении аргумента x, осуществляется “сгущение» таблицы дискретных значений. Приближение f(x) к более простой φ(x)

называется апроксимацией.

Близости этих функций добиваются путѐм введения в апроксимирующую φ(x) соответствующих свободных параметров. Если значения аргумента x расположены между узлами x0 и xn, то нахождение приближѐнного значения функции называют интерполяцией. Если значения аргумента x вычисляют вне интервала (x0; xn), то нахождение приближѐнного значения функции называют экстраполяцией.

Линейная интерполяция.

Простейшим видом интерполяции является линейная. Линейная интерполяция – частный случай интеполяции

Линейная интерполяция используется для слабоменяющихся функций на небольших интервалах.

Используя большее число точек и апроксимируя исходную функцию более сложной функцией можно уточнить полученный результат.

Тема 15. Интерполяция полиномами.

Пусть функция задана таблично. Выбранные значения x называют узлами таблицы. В общем случае они не являются равноотстоящими. Введѐм апроксимирующую функцию φ так, чтобы она совпадала с табличными значениями функции во всех узлах xi.

Такой способ называется лагранжевой интерполяцией. А условие 1 – условием Лагранжа. Ci – коэффициенты, которые надо определить из системы 1.

Выберем в качестве апроксимирующей функции полином степени n:

Достоинства интерполяции полиномами:

простота вычислений

простота дифференцирования

простота интегрирования

Задача:

Система 3 имеет решение, так как определитель не равен нулю и среди xi нет совпадающих. Независимо от формы представления полинома для заданной таблицы узлов и значений функции

Тема 18. Интерполяция полиномами Лагранжа.

Пусть в исходной таблице задается n+1 значение функции f(x) в узлах xi. Лагранж предложил следующую формулу интерполяционного полинома:

В отличие от канонического интерполяционного полинома для вычисления полинома Лагранжа не требуется предварительного вычисления коэффициентов полинома путѐм решения системы уравнений. Однако для каждого значения x полином 6 приходится рассчитывать заново, а коэффициенты в полиноме вычисляются один раз. Поэтому полиномы 6 вычисляются когда интерполяционная функция вычисляется в небольшом количестве точек xi.

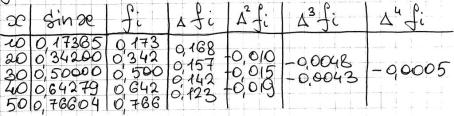
Тема 17. Метод разделенных разностей.

Более простой способ определения коэффициента ε, входящего в полином H, можно рекомендовать для случая, когда узлы заданы через равные промежутки.

Для практических расчѐтов эти разницы часто сводят в таблицы.

Такая схема вычисления коэффициента интерполяционного полинома обладает следующими преимуществом: обеспечивается меньшая погрешность в вычислении разностей при близкорасположенных узлах за счѐт наименьшего количества вычислений, а также сокращает количество обращений к элементам массивов, узлов и значений функций. НО метод справедлив только для равноотстоящих узлов.

Пример: h=10

За исходное x принимают любое x0 с коэффициеном ближе к исходной точке.

Для нахождения функции в интерполирующей точке используют только первую разность.

Количество разностей можно увеличивать до тех пор, пока их вклад не станет пренебрежимо малым.

Тема 21. Схема Горнера.

Полученные при интерполяции полиномы удобнее всего посчитать, используя схему Горнера. Для этого исходный полином записывают в виде:

Таким образом вычисление полинома сводится к последовательному вычислению. Счѐт начинается с конца.

=

−1 = −1 +

−2 = −2 + −1

1 = 1 + 2

0 = 0 + 1 =

Эта схема реализуется путѐм применения n-сложений, то есть за 2n арифметических действий (традиционный подход – за 3n-1–действий). Схема удобна ввиду своей цикличности.

Пример:

Тема 20. Интерполяция сплайнами.

Полиномиальная интерполяция не всегда даѐт удовлетворительный результат. Несмотря на выполнение условия Лагранжа интерполяционная функция может существенно отклоняться от апроксимированной кривой между узлами. При этом повышение степени полинома приводит не к уменьшению, а к увеличению погрешности. Для проведения гладких кривых через узловые значения функции успользуется сплайн интерполяции (сплайн – линейка). Гибкую линейку деформируют так, чтобы по ней можно было провести кривую через заданные точки. Недеформируемая линейка между соседними узлами проходит по линии, удовлетворяющей уравнению

(1)= 0

Если в качестве функции выбрать полином, то его степень, в соответствии с 1 должна быть не выше третьей. Этот полином называют кубическим сплайном.

Сплайн – группа сопряженных кубических многочленов в местах

сопряжения которых первая и вторая производная непрерывна.

(2) = + − −1 + − −1 2 + − −1 3

где a, b, c, d – коэффициенты сплайна, определенные из дополнительных условий; i – номер сплайна.

2)Непрерывность первой и второй производной от сплайнов в узлах

3)На концах сплайнов необходимо задавать такие условия, чтобы концы сплайна были свободны

(5)′ 0 = 0

(6)′ = 0

Задача: определить коэффициенты сплайна a, b, c и d для конкретной задачи.

Запишем 2 для i-сплайна для точки −1

−1 = + − + =

И равняется в свою очередь согласно 3 fi

(7)= −1

Продифференцируем 2 по x два раза

После определения коэффициентов находят апроксимирующую функцию на 2 в любой точке x на интервале

[x0,n].

Тема 19. Метод наименьших квадратов.

Если набор экспериментальных данных получен со значительной погрешностью, то не имеет смысла использовать интерполяцию Лагранжа полиномами и сплайнами для обработки результатов. В этом случае удобно провести апроксимирующую кривую не через экспериментальные точки, а так чтобы она сглаживала возможные «выбросы» за счѐт погрешности.

Пусть известные значения функции f и t в узлах xi получены экспериментально. Введѐм непрерывную функцию f(x) для апроксимации дискретных зависимостей f(x). В узлах эти функции будут различаться на величину

= − .

Отклонения могут быть положительные и отрицательные. Чтобы не учитывать знаки каждое отклонение возводят в квадрат и суммируют со всеми узлами.

квадратов.

Функцию φ(x) часто выбирают в виде линейной комбинации

где φi – базисные функции; Ci – коэффициенты, которые надо найти.

Условием минимизма функции является равенство нулю и еѐ первой производной. Продифферинцируем 1 по всем коэффициентам С.

Свойства матрицы:

1)Матрица Грама симметрична ( , = , );

2)Матрица является положительно-определенной, то есть при решении методом исключения Гауса можно отказаться от определения главного элемента;

3)Определитель матрицы отличен от нуля, если в качестве базиса выбраны линейно независимые функции

φk(x) и система 2 имеет единственное решение.

При обработке экспериментальных данных обычно начинают с апроксимации функции φ(x), представления одной, двумя базисными функциями. После определения коэффициентов С находят среднее квадратичное

отклонение Q по 1. Если получается, что > , то расширяют базис, добавляя новые функции, до тех пор, пока

Для формирования этой матрицы требуется определить элементы первой строки и двух последних столбцов. Остальные элементы заполняются с помощью циклического присвоения. Этот базис используется если исходные данные удаѐтся апроксимировать полиномами не выше 5 степени, иначе удобно успользовать классический полином.

Линейный вариант МНК.

На практике часто оказывается возможным ограничиться построением линейной апроксимирующей функции.