§6. Линейные и евклидовы пространства.

НЕРАВЕНСТВО КОШИ–БУНЯКОВСКОГО.

6.1. Понятия вектора, линейного пространства.

В школьных курсах математики и физики изучаются величины, которые нельзя охарактеризовать одним числом: точки и геометрические векторы в фиксированной системе координат на плоскости или в трехмерном пространстве, скорость материальной точки, сила и т.д. Однако в геометрии, механике, физике есть такие объекты, которые нельзя однозначно охарактеризовать только тремя числами, например, шар в трехмерном пространстве: положение центра (три числа) и радиус.

Есть множество объектов, для которых определены одинаковые операции, которые могут определяться по-разному, но иметь одинаковые свойства. Например: сложение матриц и сложение геометрических векторов.

Поэтому возникла необходимость описания совокупности всевозможных упорядоченных систем из nчисел, обладающих определенными свойствами.

Упорядоченная числовая строка x=(x₁, x₂,…, x_n) называетсяn-мерным вектором. Числаx_i , i=1,n, называютсякомпонентами (координатами) вектораx. Векторыx=(x₁, x₂,…, x_n)иy=(y₁, y₂,…, y_n)называютсяравными, еслиx_i= y_iдля всехi=1,n.

Операции над векторами:

Суммой двух векторовxиyбудем называть векторx+y= (x₁+y₁,x₂+y₂,…..,x_n+y_n).

Произведениемвектораx=(x₁, x₂,…, x_n)на действительное число α будем называть векторαx=(αx₁,αx₂,…,αx_n).

Свойства операций над векторами:

1) x+y= y+x(коммутативность),

2) x+ (y+z) =(x+y)+z(ассоциативность),

3) существует единственный вектор 0, такой, что для всех векторов x+ 0 = x,

4) для любого xсуществует единственный вектор (x) такой, чтоx+(x)=0,

5) α(x+y)=αx+αy, αR,

6) (α)x=αxx, αдействительные числа,

7) αx=αx,

8) для любого x 1 x=x.

Вектор (x)= =(–x₁, x₂,…,– x_n) называетсяпротивоположнымдля вектораx=(x₁, x₂,…, x_n). Вектор 0=(0,0,…,0) называется нулевым вектором.

Множество всех n-мерных векторов с действительными компонентами, рассматриваемая с определенными в ней операциями сложения векторов и умножения вектора на число, называетсялинейным (векторным) пространством.ОбозначаетсяL.

Пример: Множество многочленов степени n.

6.2. Линейная зависимость векторов. Базис.

Выражение вида называетсялинейной комбинациейвекторовс коэффициентами.

Система векторов называетсялинейно зависимой, если существуют числане все равные нулю, причем выполняется равенство

=0. (1)

Если (1) выполняется лишь в случае, когда , то векторы называютсялинейно независимыми.

Базисом в пространстве L называется упорядоченная, конечная система векторов, если:

1) она линейно независима,

2) каждый вектор пространства Lявляется линейной комбинацией векторов этой системы.

Пусть векторы составляют базис. Тогда любой векторможет быть представлен единственным образом в виде линейной комбинации векторовследующим образом:

………………………………………………………………………(2)

Выражение (2) называется разложением вектора по базису. Тогданазываютсякоординатами векторав этом базисе.

Теорема 1. Если в линейном пространствеLсуществует базис изnвекторов, то любой другой базис в этом пространстве состоит из того же числа векторов.

Доказательство:(от противного)

Пусть в пространстве Lсуществуют два базисаи, причем. Каждый из векторов базисамы разложим по базису.

……………………………..

.

Составим матрицу, столбцами которой будут координаты векторов в базисе:

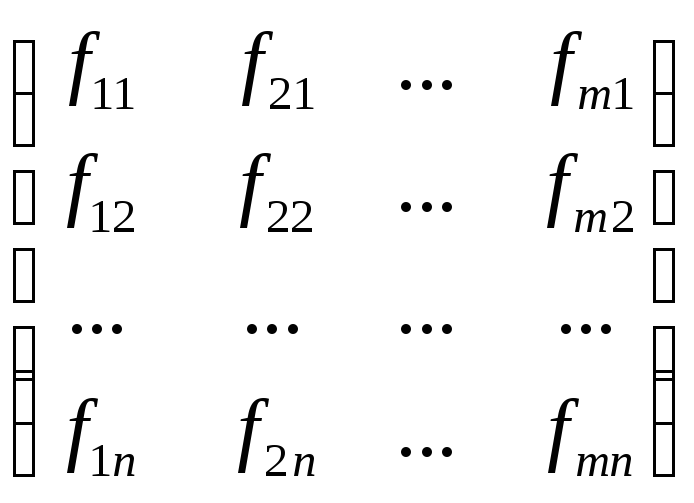. Размерность этой матрицыmn. Ее ранг не превосходитn. По теореме о ранге матрицы столбцы матрицы линейно зависимы, а, следовательно, зависимы и векторы, т.е. они не могут составлять базис.

Линейное пространство, в котором существует базис из nвекторов, называетсяn-мерным, числоn–размерностью пространства. Обозначается. Размерность нулевого пространства по определению считается равным нулю.

Теорема 2:Вn-мерном пространстве каждая упорядоченная система изn линейно независимых векторов является базисом. (без доказательства).

Рассмотрим переход от одного базиса к другому. Пусть в n-мерном пространстве даны два базисаВ:иВ^’:. Разложим каждый вектор базисаВ^’ по базисуВ:

,

, (3)

…………………………………,

.

Компоненты _ijможно записать в виде квадратной матрицы порядкаn.

. Столбцы матрицы – это координаты векторовв базисеВ. Поэтому столбцы матрицыТлинейно независимы и, значит, |Т|≠0.

Матрица Т,i-ый столбец которой есть координатный столбец векторапо базису, называется матрицей перехода от базисаВк базисуВ^’. Равенство (3) можно переписать в матричных обозначениях:

или ,……………………………………………………………………………(4)

где ,.

Умножая равенство (4) справа на , получим. Т.е. , где- матрица перехода от базисаВ^’к базисуВ.

Определим связь компонент одного и того же вектора в двух базисахВ и В^’.

Разложение в старом базисе В:,

в новом базисе B^’:.

Приравниваем =.

В матричном виде: , где,.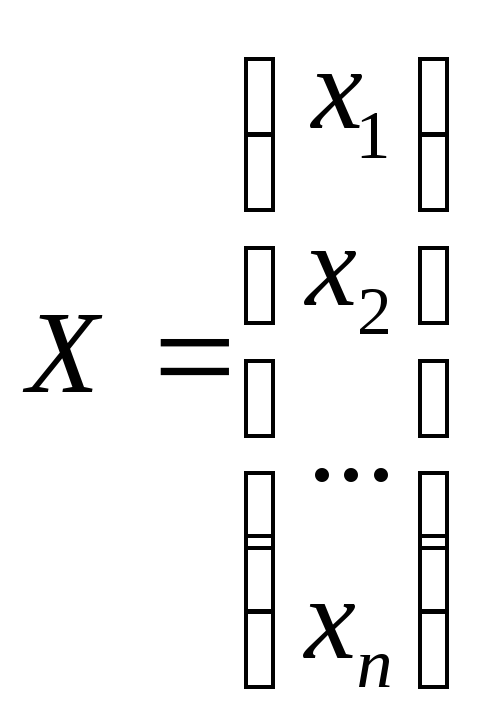

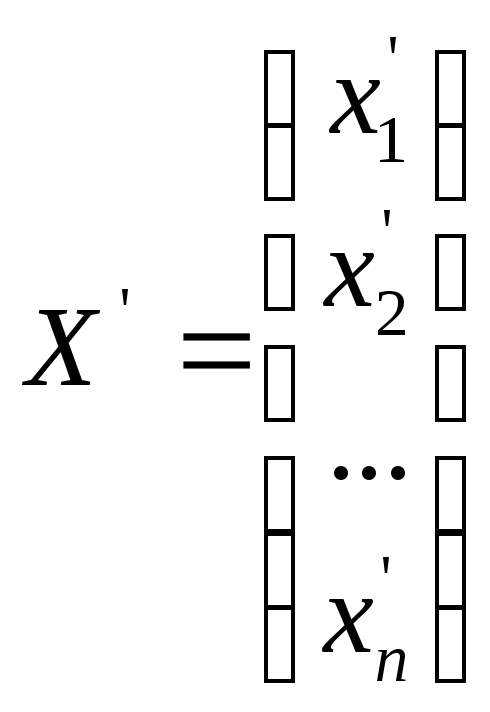Но  . (5)

Это формула перехода от новых координат вектора к старым.

Умножим слева на (|T|≠0). Получим. Это формула перехода от старых координат векторак новым.

Пример: 1)

2)