
- •Глава 1. Линейная алгебра.
- •§1. Матрицы и действия над ними.
- •1.1. Понятие матрицы
- •1.2. Основные операции над матрицами и их свойства.
- •§2. Определители.
- •2.1. Понятие определителя.
- •2.2. Свойства определителей.
- •§3. Обратная матрица.
- •3.1. Понятие обратной матрицы. Теорема об обратной матрице.
- •3.2. Метод элементарных преобразований.
- •§4. Системы линейных уравнений. Методы решения.
- •4.1. Понятие системы линейных уравнений.
- •4.2. Матричный способ решения слу.
- •4.3. Формулы Крамера.
- •§5. Ранг матрицы. Теорема кронекера-капелли. Решение произвольных методов гаусса. Однородные системы.
- •5.1.Ранг матрицы.
- •5.2. Методы нахождения ранга матрицы.
- •5.3. Теорема Кронекера-Капелли.
- •5.4.Решение произвольных систем методом Гаусса.
- •5.5. Однородные системы.
- •§6. Линейные и евклидовы пространства.
- •6.1. Понятия вектора, линейного пространства.
- •6.2. Линейная зависимость векторов. Базис.
- •6.3. Евклидовы пространства. Неравенство Коши-Буняковского.
4.2. Матричный способ решения слу.
Рассмотрим случай, когда m=nи матрицаА невырожденная, т.е. СЛУ квадратная и |А|≠0.
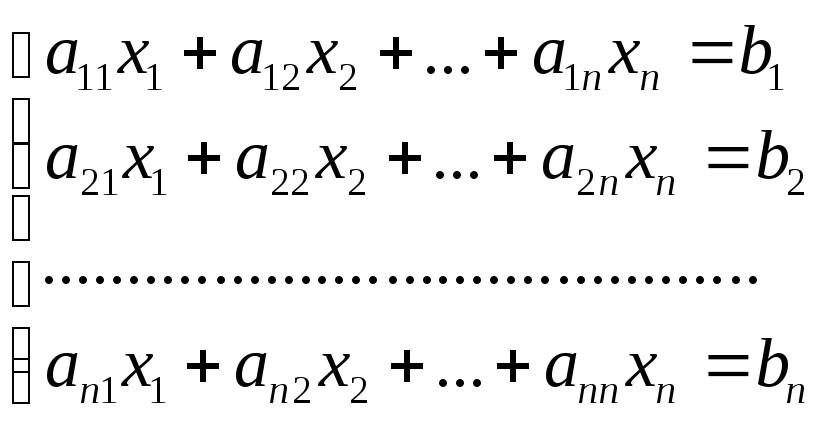 (2)
(2)
Систему можно переписать в матричном
виде: АX=B
(3),
гдеА =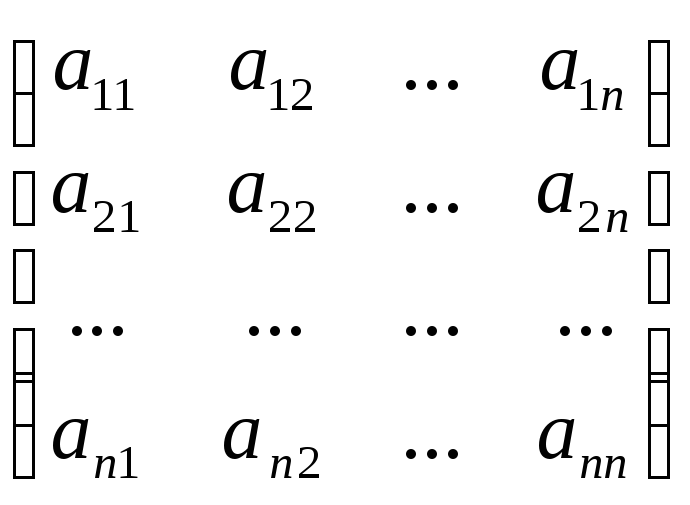 – основная матрица системы,
– основная матрица системы,
X=![]() столбец неизвестных,B=
столбец неизвестных,B=![]() – столбец свободных членов.
– столбец свободных членов.
Так как определитель матрицы |А|≠0, то существует обратная матрицаА-1. Предположим, что существует решение системы (2), т.е. существует столбецX, обращающий в тождество матричное уравнение (3). Умножим (3) слева на обратную матрицуА-1, получим:
А-1(АX)= А-1В.
В силу сочетательного свойства произведения матриц, а также равенства A-1А=Е, получаем:
А-1(АX)=(A-1А)X=EX=X.
Таким образом X= А-1B матричныйметодрешения СЛУ (2)
Проверка:Легко проверить, что столбецX, определяемый соотношением (5) является решением матричного уравнения (3), т.е. при подстановке в это уравнение обращает его в тождество. В самом деле:AX=A (А-1B) = (A-1А)B=EB=B =B=B тождество.
Пример:
4.3. Формулы Крамера.
Рассмотрим квадратную СЛУ (2). Если определитель матрицы системы отличен от нуля, т.е. |А|≠0, то система имеет и притом одно решение. Это решение находится по формулам:
![]() (j=1,n),
гдеопределитель матрицы системы (главный
определитель),jопределитель,
получаемый из главного определителя
заменойjго
столбца столбцом свободных членов.
(j=1,n),
гдеопределитель матрицы системы (главный
определитель),jопределитель,
получаемый из главного определителя
заменойjго
столбца столбцом свободных членов.
j =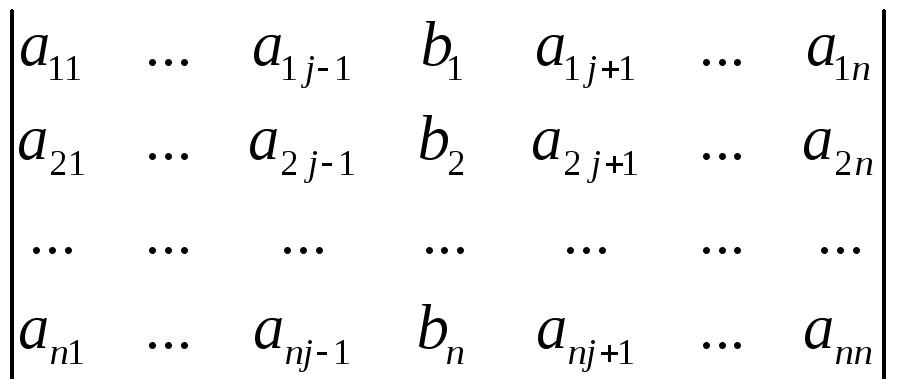
jый столбец
Этот определитель называется вспомогательным.
Доказательство:
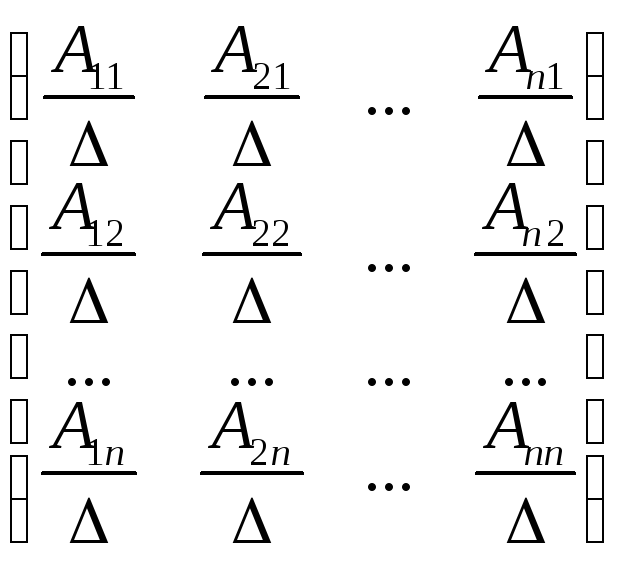
Запишем решение СЛУ X= А-1Bв развернутом виде
![]() =
=
![]() =
=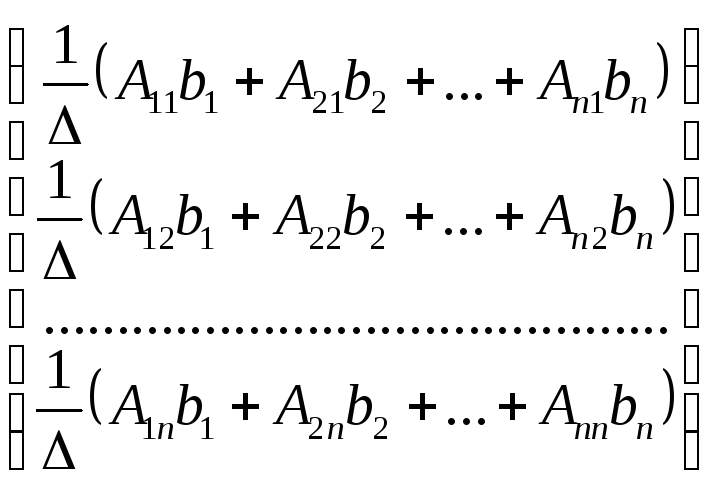 =
=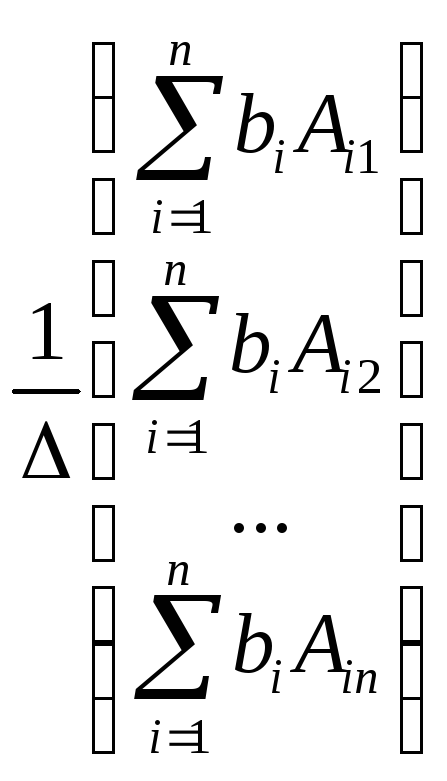 .
.
Таким образом
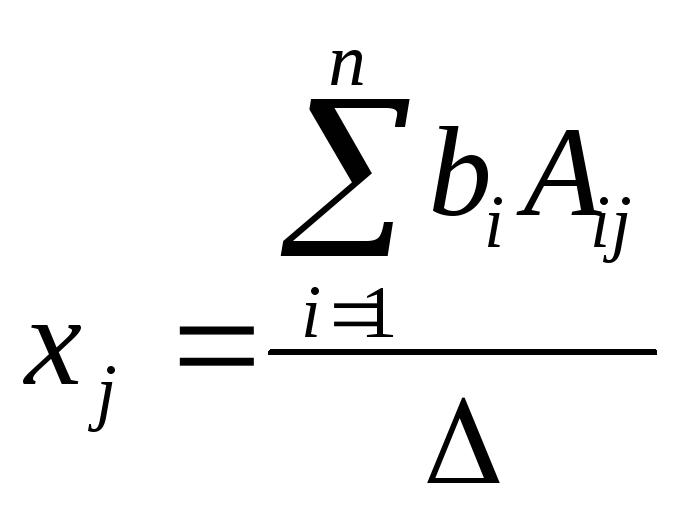 в
числителе записано разложение
вспомогательного определителя поj-ому
столбцу (по определению определителяn-го порядка)
в
числителе записано разложение
вспомогательного определителя поj-ому
столбцу (по определению определителяn-го порядка)![]() (j=1,n).
(j=1,n).
Докажем единственность.
Пусть существуют два различных решения
![]() и
и![]() .
Запишем систему (2) в видеx1a1+x2a2+…+xnan=B,
гдеa1=
.
Запишем систему (2) в видеx1a1+x2a2+…+xnan=B,
гдеa1=![]() ,a2=
,a2=![]() ,…,an=
,…,an=![]() .
.
Подставляем решения в систему:
![]() )
)
ˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉˉ
![]() .
.
Так как хотя бы одна из разностей
![]() ,
то мы получаем, что столбцыа1,а2,…,аn
линейно зависимы, т.е. |А|=0, а это
противоречит условию теоремы.
,
то мы получаем, что столбцыа1,а2,…,аn
линейно зависимы, т.е. |А|=0, а это
противоречит условию теоремы.
Основное значение формул Крамерасостоит в том, что они дают явное выражение для решения квадратных СЛУ через коэффициенты уравнения и свободные члены.
Пример: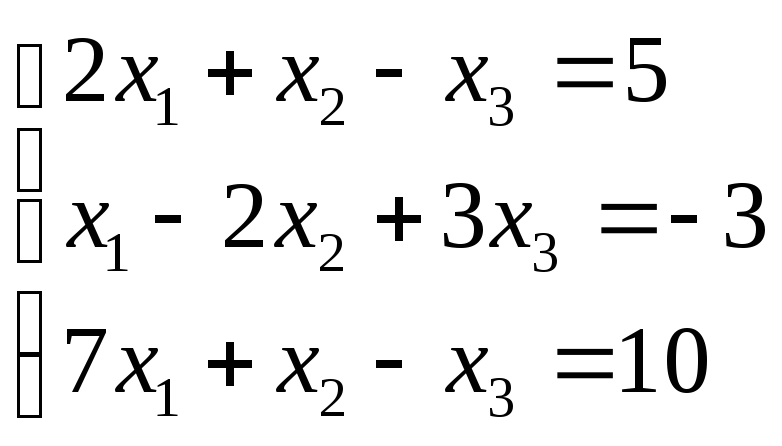
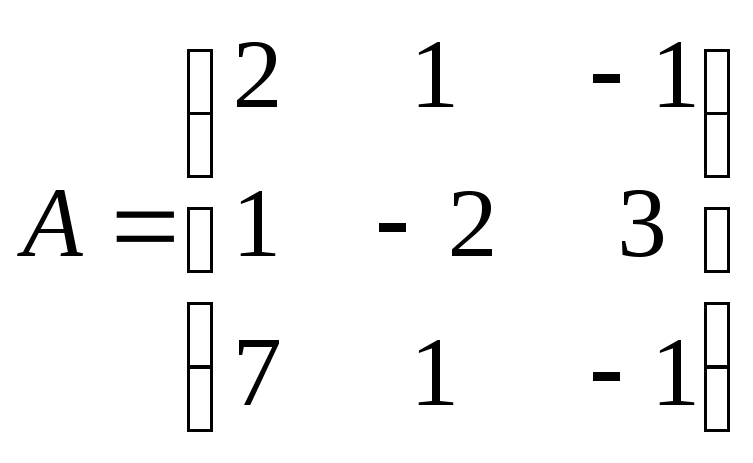
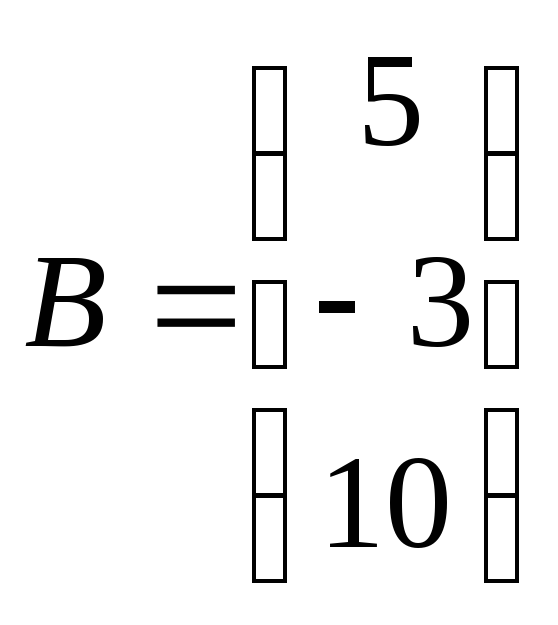
=5 1=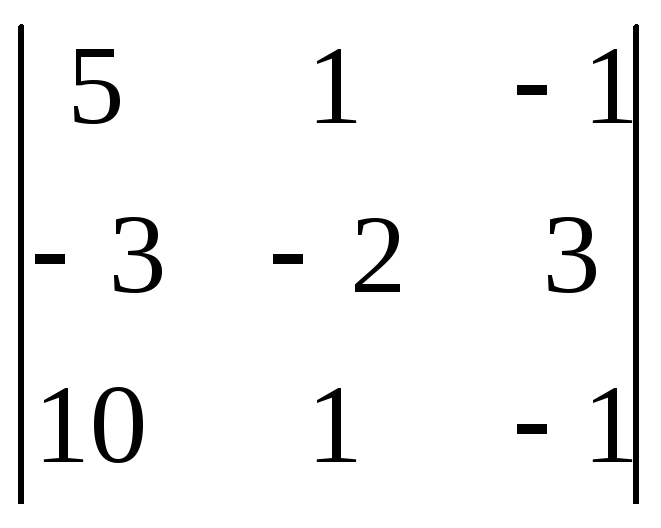 = 52=
= 52=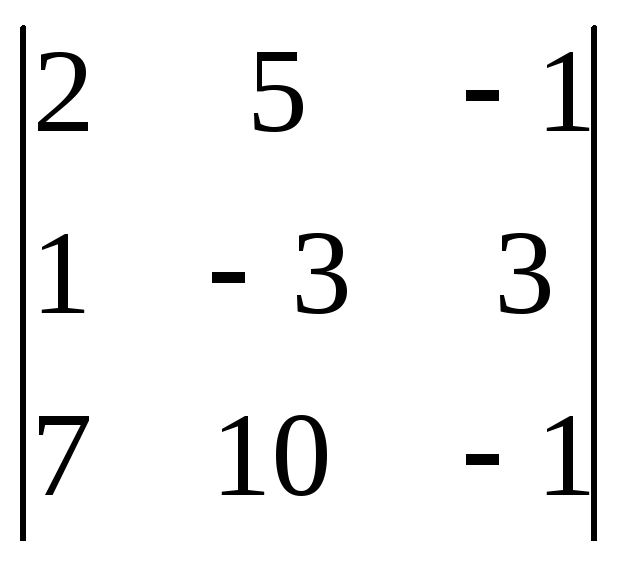 = 253=
= 253=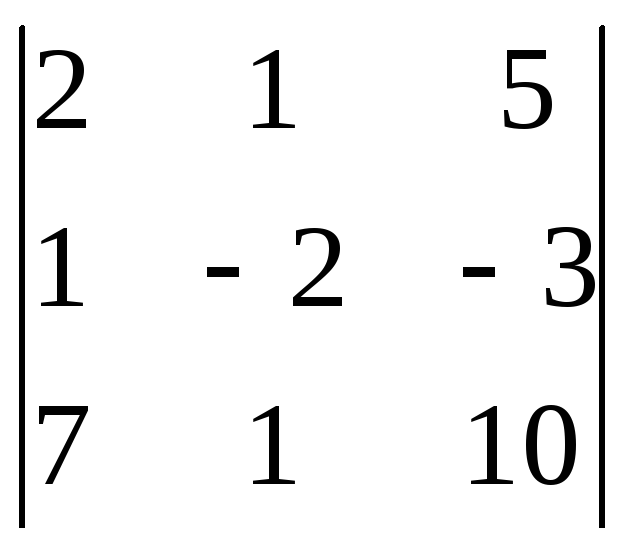 = 10
= 10
![]() .
.
§5. Ранг матрицы. Теорема кронекера-капелли. Решение произвольных методов гаусса. Однородные системы.
5.1.Ранг матрицы.
Рассмотрим произвольную матрицу:
А=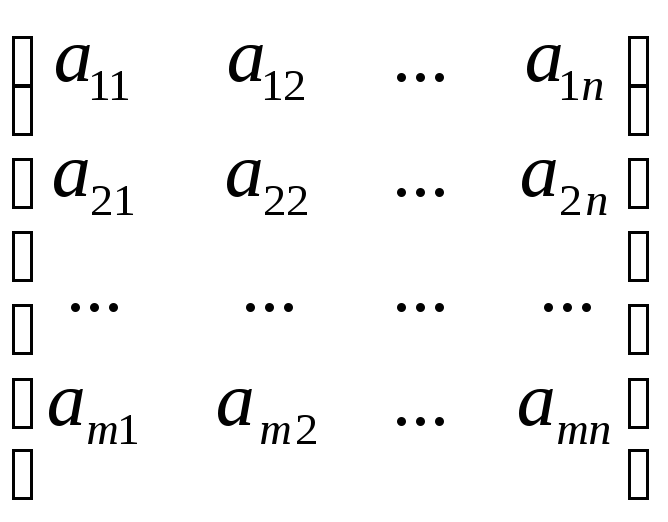 (1)
(1)
Строки
![]() назовемлинейнозависимыми, если
найдутся такие числа
назовемлинейнозависимыми, если
найдутся такие числа![]() не все равные нулю, что справедливы
равенства
не все равные нулю, что справедливы
равенства
![]() (j=1,n)
или
(j=1,n)
или![]() (2), где
(2), где![]() =(0,0,…,0).
=(0,0,…,0).
Строки
![]() называютсялинейно независимыми,
если равенство (2) выполняется лишь в
случае, когда
называютсялинейно независимыми,
если равенство (2) выполняется лишь в
случае, когда![]() .
.
Выражение
![]() называетсялинейной комбинацией.
называетсялинейной комбинацией.
Для того, чтобы
![]() были линейно зависимыми, необходимо и
достаточно, чтобы одна из этих строк
являлась линейной комбинацией остальных
строк.
были линейно зависимыми, необходимо и
достаточно, чтобы одна из этих строк
являлась линейной комбинацией остальных
строк.
Пример:
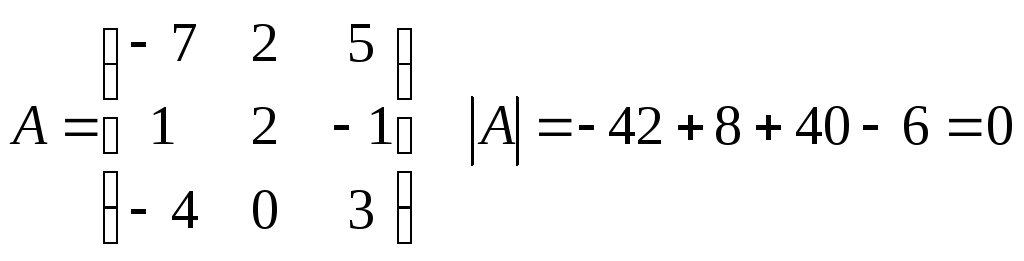 – первая строка – линейная комбинация
остальных двух
– первая строка – линейная комбинация
остальных двух![]() .
.
Выделим в матрице (1) k строк и k столбцов (k min(m,n)).Миноромk-го порядкаматрицыAназывается определитель k-го порядка, составленный из элементов, стоящих на пересечении выделенных строк и столбцов. Наибольший из порядков миноров данной матрицы, отличных от нуля, называетсярангом матрицы. Обозначения r, r(A), rang A. Очевидно 0rang A min(m,n). Всякий минорr+1-го и более высокого порядка (если таковые существуют) равен нулю. Минор, порядок которого определяет ранг матрицы, называетсябазисным минором. Строки и столбцы, на пересечении которых стоит базисный минор, называются соответственнобазисными строкамиибазисными столбцами. У матрицы может быть несколько базисных миноров.
Пример: найти ранг матрицыA= .M3=0,M2=
.M3=0,M2=![]() =15r(A)=2.
=15r(A)=2.
Теорема о базисном миноре: Базисные строки (базисные столбцы) линейно независимы. Любая строка (любой столбец) матрицыАявляется линейной комбинацией базисных строк (базисных столбцов).
Теорема о ранге матрицы: Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) в этой матрице.
Свойства ранга матрицы:
1) При транспонировании матрицы ее ранг не меняется;
2) При вычеркивании из матрицы нулевой строки (столбца) ранг матрицы не меняется;
3) Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
