
- •Введение
- •1. Основные понятия и определения
- •Вопросы и задания для самопроверки
- •2. Статическая устойчивость электроэнергетических
- •2.2. Векторная диаграмма для явнополюсного синхронного генератора в простейшей электроэнергетической системе
- •2.3. Характеристика мощности при сложной связи генератора с приемной системой
- •2.4. Максимальные и предельные нагрузки
- •2.5. Требования, предъявляемые к режимам
- •2.6. Характеристики режимов простейшей электроэнергетической системы при синхронной скорости вращения генератора
- •2.7. Простейшая оценка устойчивости установившегося режима. Энергетический критерий
- •2.8. Практический критерий статической устойчивости для простейшей ээс
- •2.9. Практический критерий статической устойчивости для асинхронных двигателей
- •2.10. Коэффициенты запаса статической устойчивости
- •2.11. Общая характеристика и дифференциальные уравнения регулирования возбуждения генератора
- •Вопросы и задания для самопроверки
- •3. Динамическая устойчивость ээс
- •3.1. Допущения, принимаемые при анализе динамической устойчивости
- •3.2. Уравнение движения ротора синхронной машины
- •3.3. Оценка динамической устойчивости при переходе от одного режима к другому
- •3.4. Энергетические соотношения, характеризующие движение ротора генератора
- •3.5. Способ площадей и вытекающие из него критерии динамической устойчивости
- •3.6. Определение предельного угла отключения короткого замыкания
- •3.7. Определение предельного времени отключения аварии
- •3.8. Проверка устойчивости при наличии трехфазного или пофазного автоматического повторного включения лэп
- •3.9. Применение способа площадей при анализе действия автоматического регулирования
- •3.10. Условия успешной синхронизации
- •3.11. Способ площадей при исследовании устойчивости двух станций
- •3.12. Метод последовательных интервалов
- •3.13. Расчет динамической устойчивости систем с несколькими генераторными станциями
- •3.14. Динамическая устойчивость неявнополюсного генератора, работающего на шины бесконечной мощности
- •3.15. Динамическая устойчивость явнополюсного генератора при учете электромагнитных процессов
- •Вопросы и задания для самопроверки
- •4. Асинхронные режимы, ресинхронизация и результирующая устойчивость
- •4.1. Общая характеристика асинхронных режимов
- •В электроэнергетических системах
- •4.2. Возникновение асинхронного режима
- •4.3. Задачи, возникающие при исследовании асинхронных режимов
- •4.4. Параметры элементов электроэнергетических систем при асинхронных режимах
- •4.4.1. Генераторы
- •4.4.2. Первичные двигатели
- •4.4.3. Нагрузка
- •4.4.4. Линии электропередачи, сеть
- •4.5. Выпадение из синхронизма, асинхронный ход синхронных машин
- •4.6. Вхождение в синхронизм асинхронно работающих генераторов
- •4.7. Основные сведения об устройствах ликвидации асинхронного режима
- •4.8. Способы ликвидации асинхронных режимов в энергосистемах
- •4.9. Основные принципы выявления асинхронного хода
- •Вопросы и задания для самопроверки
- •5. Мероприятия по повышению надежности, улучшению устойчивости и качества переходных процессов ээс
- •5.1. Постановка задачи
- •5.2. Улучшение характеристик основных элементов электроэнергетической системы
- •5.3. Дополнительные устройства для улучшения устойчивости
- •5.4. Мероприятия режимного характера
- •Вопросы и задания для самопроверки
- •Библиографический список
3.14. Динамическая устойчивость неявнополюсного генератора, работающего на шины бесконечной мощности
При учете переходных
электромагнитных процессов, возникающих
из-за изменения параметров системы или
действия устройств автоматического
регулирования возбуждения генераторов,
к дифференциальному уравнению
электромеханического состояния каждой
станции рассматриваемой системы
добавляются дифференциальные уравнения
ее электромагнитного состояния. В общем
случае это могут быть уравнения
Горева-Парка, в более простых случаях
− упрощенные уравнения, дающие соотношение
между переходной ЭДС
![]() и ЭДС
и ЭДС![]() или и смещением векторов этих ЭДС по
отношению к ЭДС других станций (углы
или и смещением векторов этих ЭДС по
отношению к ЭДС других станций (углы![]() ).
).
Предполагая
генератор неявнополюсным и замещая его
синхронным индуктивным сопротивлением
![]() ,
можно определить собственную и взаимную
проводимости
,
можно определить собственную и взаимную
проводимости![]() и
и![]() ветвей генератора в схеме замещения и
дополнительные углы
ветвей генератора в схеме замещения и
дополнительные углы![]() и
и![]() (для схемы с шунтирующим сопротивлением,
включенным в расчетной точке КЗ), рис.
3.23.
(для схемы с шунтирующим сопротивлением,
включенным в расчетной точке КЗ), рис.
3.23.
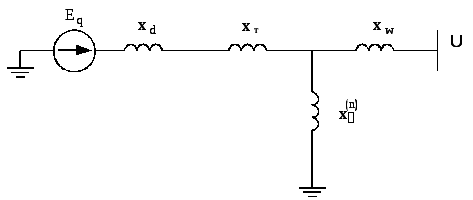
Рис. 3.23. Схема замещения аварийного режима простейшей ЭЭС
с неявнополюсным генератором
Примем
ось отсчета аргументов векторов
совпадающей с вектором напряжения шин
приемной системы, т.![]() е.
е.
![]() .
Вектор ЭДС генератора
.
Вектор ЭДС генератора![]() опережает вектор напряжения
опережает вектор напряжения![]() на
угол
на
угол![]() .
Величина ЭДС как в первый момент КЗ, так
и в течение всего переходного процесса
претерпевает изменения, которые должны
быть учтены в расчете. Ток, отдаваемый
генератором в сеть, равен
.
Величина ЭДС как в первый момент КЗ, так
и в течение всего переходного процесса
претерпевает изменения, которые должны
быть учтены в расчете. Ток, отдаваемый
генератором в сеть, равен
![]() .
.
Из
векторной диаграммы (рис. 3.24) нетрудно
найти продольную составляющую тока
статора
![]() ,проецируя
вектор тока
,проецируя
вектор тока
![]() на
направление, перпендикулярное вектору
на
направление, перпендикулярное вектору
![]() :
:
![]() .
.
Подставим
это выражение для
![]() в
известное соотношение
в
известное соотношение
![]()
Получаем
![]()
или
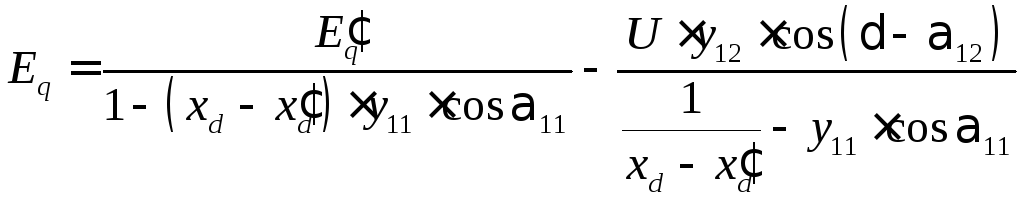 (3.51)
(3.51)

Рис. 3.24. Векторная диаграмма неявнополюсного генератора
Это
уравнение связывает ЭДС ![]() и
и ![]() и
угол
и
угол
![]() в рассматриваемых условиях.
в рассматриваемых условиях.
Кроме того, справедливо общее дифференциальное уравнение (уравнение обмотки возбуждения)
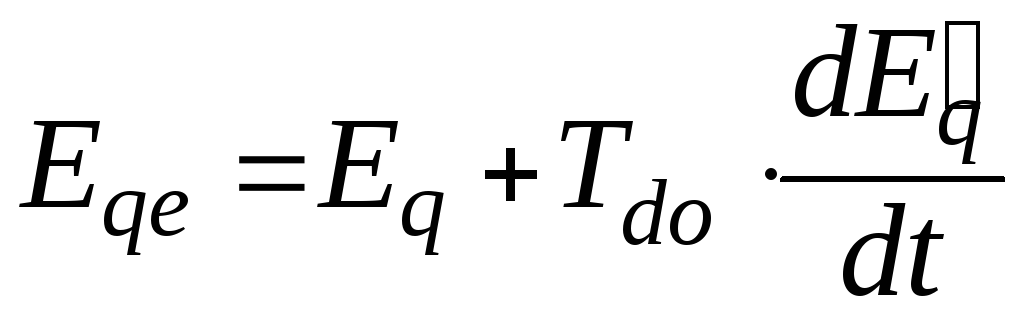 .(3.52)
.(3.52)
Это
уравнение, решенное в конечных разностях,
позволяет найти изменения ЭДС
![]() за
интервал времени
за
интервал времени
![]() при
расчете методом последовательных
интервалов:
при
расчете методом последовательных
интервалов:
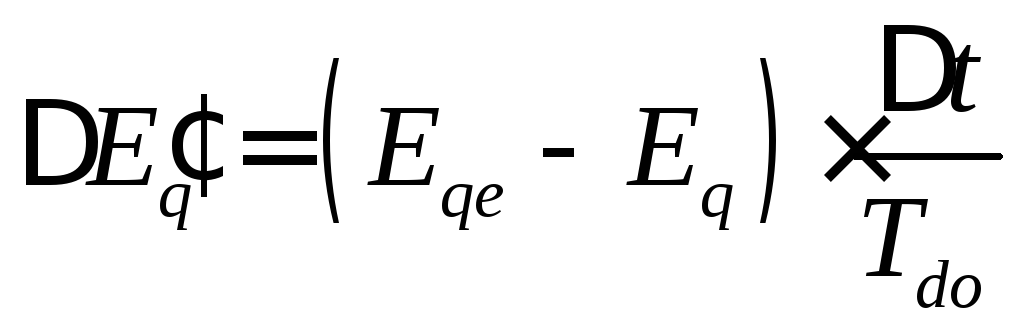 (3.53)
(3.53)
При
этом значения ![]() берутся
средними в заданном интервале времени
и определяются по кривым, соответствующим
заданному изменению напряжения
возбудителя.
берутся
средними в заданном интервале времени
и определяются по кривым, соответствующим
заданному изменению напряжения
возбудителя.
За
рассматриваемый интервал времени
![]() изменяется также ЭДС
изменяется также ЭДС![]() и угол
и угол
![]() .
Изменение угла подсчитывают обычным
способом.
.
Изменение угла подсчитывают обычным
способом.
ЭДС ![]() в
течение интервала
в
течение интервала
![]() изменяется
в связи с затуханием свободных токов,
возникших в момент нарушения режима, и
появлением токов, наведенных при
изменении угла. Значение
изменяется
в связи с затуханием свободных токов,
возникших в момент нарушения режима, и
появлением токов, наведенных при
изменении угла. Значение ![]() в
начале следующего интервала времени
определяется согласно (3.51). При этом
значения ЭДС
в
начале следующего интервала времени
определяется согласно (3.51). При этом
значения ЭДС ![]() и
угла
и
угла
![]() ,
входящие в это уравнение, должны быть
взяты соответствующими началу интервала.
,
входящие в это уравнение, должны быть
взяты соответствующими началу интервала.
Расчет динамической устойчивости для неявнополюсной машины включает следующие этапы:
1. В
нормальном режиме работы определяют
значение мощности
![]() ,
угла
,
угла
![]() ,
продольной составляющей ЭДС за переходным
индуктивным сопротивлением
,
продольной составляющей ЭДС за переходным
индуктивным сопротивлением
![]() ,
ЭДС
,
ЭДС
![]() и
соответствующее ей напряжение на выходе
возбудителя
и
соответствующее ей напряжение на выходе
возбудителя
![]() .
.
2.
Определяют собственные и взаимные
проводимости ветви генератора для
аварийной схемы (для генераторов в схеме
берется синхронное индуктивное
сопротивление
![]() ).
).
3. При
наличии в системе возбуждения генератора
режима форсировки возбуждения строят
кривую изменения напряжения на выводах
возбудителя
![]() и
соответствующих значений вынужденной
ЭДС
и
соответствующих значений вынужденной
ЭДС ![]() (графики отличаются масштабами, рис.
3.25).
(графики отличаются масштабами, рис.
3.25).
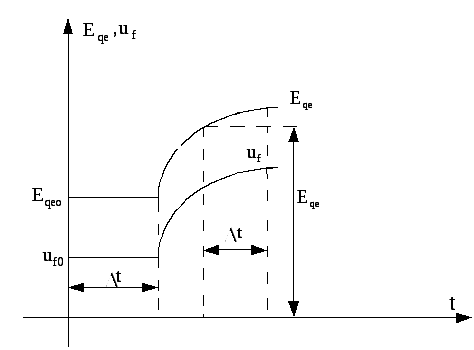
Рис. 3.25. Изменение вынужденной
составляющей ЭДС
![]() и напряжения возбуждения
и напряжения возбуждения![]() в течение переходного процесса
в течение переходного процесса
4. По
уравнению (3.51) определяют значение ЭДС
для первого момента нарушения режима
работы (значения ![]() и
и
![]() берут из нормального режима, т. е.
принимая
берут из нормального режима, т. е.
принимая![]() и
и
![]() )
)
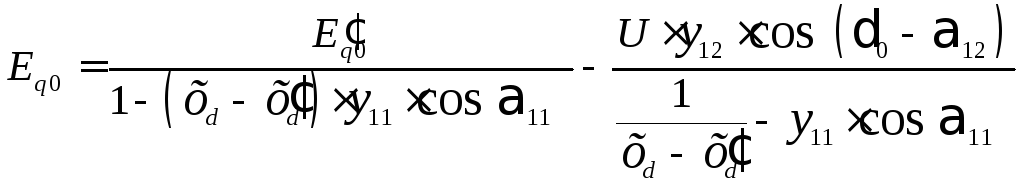
5. По
уравнению (3.53) находят изменение ЭДС ![]() в
течение первого интервала времени, где
в
течение первого интервала времени, где
![]() −
среднее
значение вынужденной ЭДС
−
среднее
значение вынужденной ЭДС ![]() за
рассчитываемый интервал времени (по
графику).
за
рассчитываемый интервал времени (по
графику).
6.
Определяют значение ![]() в
начале следующего интервала времени
в
начале следующего интервала времени
![]() .
.
7. Определяют активную мощность, отдаваемую генератором в начале данного интервала
![]() .
.
8. Находят избыток мощности генератора
![]() .
.
9. Определяют изменение угла за рассматриваемый интервал времени:
а) для первого интервала
![]() ;
;
б) для последующих интервалов
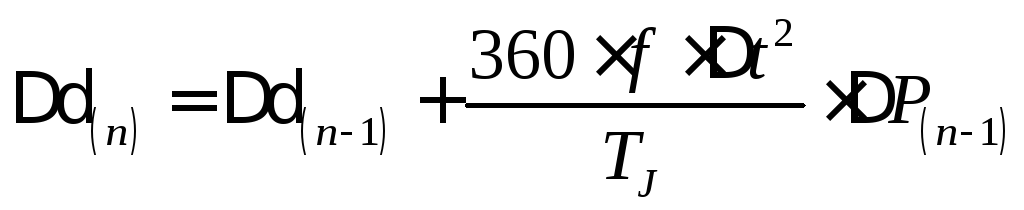 ;
;
в) для интервала, в начале которого отключается повреждение
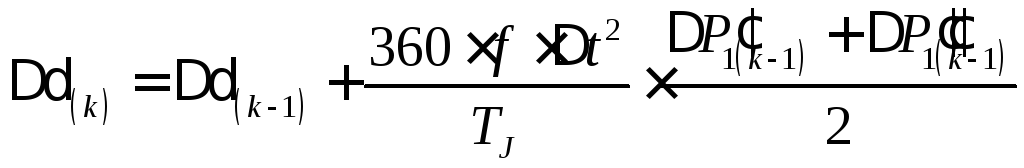 ,
,
где
![]() −
избыток мощности до отключения
поврежденной цепи;
−
избыток мощности до отключения
поврежденной цепи; ![]() −
избыток мощности после отключения.
−
избыток мощности после отключения.
10. Находят угол в начале следующего интервала
![]() .
.
Таким
образом получают значение ![]() и
угла
и
угла
![]() в начале следующего интервала. По этим
значениям можно вновь найти значение
ЭДС
в начале следующего интервала. По этим
значениям можно вновь найти значение
ЭДС![]() (пункт
4) и вновь повторить расчет для нового
интервала. Все формулы, за исключением
формулы изменения угла, остаются
неизменными − меняется лишь индекс
интервала. Уравнение изменения угла в
последующих интервалах (за исключением
первого) несколько отличается от
указанных. Вид остальных уравнений при
отключении аварии остается неизменным,
меняются лишь обобщенные параметры −
значение собственных и взаимных
проводимостей ветви генератора.
(пункт
4) и вновь повторить расчет для нового
интервала. Все формулы, за исключением
формулы изменения угла, остаются
неизменными − меняется лишь индекс
интервала. Уравнение изменения угла в
последующих интервалах (за исключением
первого) несколько отличается от
указанных. Вид остальных уравнений при
отключении аварии остается неизменным,
меняются лишь обобщенные параметры −
значение собственных и взаимных
проводимостей ветви генератора.
Расчеты по выявлению характера переходного процесса очень трудоёмкие, поэтому рассмотренный алгоритм составляется в виде программы для ЭВМ.
