
- •ГЕОДЕЗИЯ
- •Предисловие
- •ЛЕКЦИЯ № 1
- •ЛЕКЦИЯ № 2
- •2.1. Понятие о фигуре Земли
- •2.2. Метод проекции в геодезии
- •2.4. Определение положения точек земной поверхности
- •ЛЕКЦИЯ № 3
- •3.1. Понятие о зональной системе плоских прямоугольных координат
- •3.2. Ориентирование линий
- •3.3. Прямая и обратная геодезические задачи
- •ЛЕКЦИЯ № 4
- •4.1. Понятие о картах, планах и профилях. Масштабы
- •4.2. Разграфка и номенклатура топографических карт
- •ЛЕКЦИЯ № 5
- •5.1. Условные знаки топографических карт и планов
- •5.2. Изображение рельефа на картах и планах
- •ЛЕКЦИЯ № 6
- •6.1. Перечень задач, решаемых с помощью карт и планов
- •6.2. Примеры решения задач по карте и плану
- •6.3. Цифровые топографические карты
- •ЛЕКЦИЯ № 7
- •ЛЕКЦИЯ № 8
- •8.2. Типы теодолитов
- •ЛЕКЦИЯ № 9
- •9.1. Поверки и юстировки теодолитов
- •9.2. Измерение горизонтальных углов
- •ЛЕКЦИЯ № 10
- •10.1. Измерение вертикальных углов
- •10.2. Погрешности измерения углов и меры по их минимизации
- •10.3. Измерение магнитного азимута
- •ЛЕКЦИЯ № 11
- •11.1. Обзор средств и методов измерения расстояний
- •11.2. Механические приборы для измерения расстояний
- •11.3. Оптические дальномеры
- •ЛЕКЦИЯ № 12
- •12.1. Понятие о государственных геодезических сетях
- •12.3. Съемочное обоснование
- •ЛЕКЦИЯ № 13
- •13.1. Линейно-угловые ходы, их виды
- •13.2. Привязка линейно-угловых ходов
- •13.3. Привязка линейно-углового хода к стенным маркам
- •13.4. Понятие о системе линейно-угловых ходов
- •13.5. Геодезические засечки
- •ЛЕКЦИЯ № 14
- •14.1. Теодолитные ходы
- •14.2. Съемка контуров. Вспомогательный прибор – экер
- •ЛЕКЦИЯ № 15
- •15.1. Геометрические способы определения площади
- •15.2. Аналитический способ определения площади
- •15.3. Определение площади полярным планиметром
- •15.4. Определение площади по плану посредством палетки
- •15.5. Уравнивание площадей
- •ЛЕКЦИЯ № 16
- •16.1. Тригонометрическое нивелирование
- •ЛЕКЦИЯ № 17
- •17.1. Приборы для геометрического нивелирования
- •17.2. Поверки и юстировки оптико-механических нивелиров
- •ЛЕКЦИЯ № 18.
- •18.1. Технология прокладки ходов технического нивелирования
- •ЛЕКЦИЯ № 19
- •19.1. Подготовительные работы для тахеометрической съемки
- •19.2. Тахеометрическая съемка посредством теодолита
- •19.3. Понятие о тахеометрической съемке при помощи электронных тахеометров
- •19.5. Высотные тахеометрические ходы при помощи теодолита
- •ЛЕКЦИЯ № 20
- •20.1 Нивелирование по квадратам
- •20.2. Другие способы нивелирования поверхности
- •20.3. Составление топографического плана
- •ЛЕКЦИЯ № 21.
- •21.1. Основы мензульной съемки
- •21.2. Устройство и поверки мензульного комплекта
- •21.3. Поверки мензульного комплекта
- •21.4. Кипрегель-автомат
- •21.7. Подготовка планшета и мензулы к работе
- •21.8. Производство мензульной съемки
- •ЛЕКЦИЯ № 22.
- •22.1. Понятие о космических съемках
- •22.2. Аэрофотосъемка
- •СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ УЧЕБНОЙ ЛИТЕРАТУРЫ
и геометрического нивелирования
Назначение нивелирования. Нивелирование – это измерение превышений и определение высотных координат точек. Данные нивелирования необходимы при осуществлении многих видов научных исследований, например, в геодезическом мониторинге вертикальных смещений земной поверхности тектонического характера и техногенного происхождения (от извлечения жидких и твердых ископаемых). Нивелирование представляет необходимую составляющую топографических съемок, геодезических изысканий для строительства жилых и промышленных зданий, гидроэлектростанций, водохранилищ, каналов, дорог, трубопроводов и других сооружений. Нивелирные измерения предусматриваются технологиями строительства практически всех видов сооружений.
Применяются следующие виды нивелирования: геометрическое, тригонометрическое, спутниковое, гидростатическое, механическое. В данной лекции рассматриваются сущность и методы тригонометрического и геометрического нивелирования.
16.1. Тригонометрическое нивелирование
Тригонометрическое нивелирование между двумя пунктами А и В включает измерение расстояния и угла наклона между ними (рис. 16.1) с последующим вычислением превышения h по тригонометрическим формулам. Над пунктом А ставят теодолит, на пункт В – рейку или веху. На рейке или вехе отмечают точку визирования W и измеряют высоту визирования υ = WВ. Над пунктом А измеряют высоту прибора i = JА. Теодолитом измеряют угол наклона ν линии JW. Наклонное расстояние JW = D определяют, например, светодальномером или оптическим дальномером.
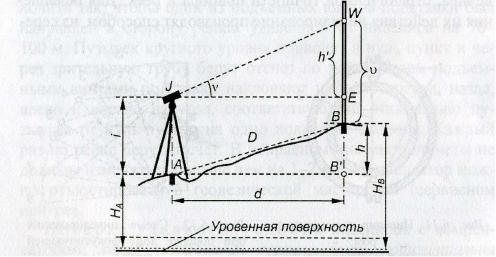
Рис. 16.1. Тригонометрическое нивелирование
Из треугольника JWЕ вычисляют тригонометрическую часть превышения (неполное превышение) ЕW = h'. Вертикальный отрезок WВ' = h + υ = h' + i, отсюда искомое полное превышение
|
h = h' + i – |
υ, |
(16.1) |
При |
расстояниях D ≥ 200 м в определяемом превышении h учитывают по- |
||
правку f |
на кривизну Земли и рефракцию, следовательно |
|
|
|
h = h' +i – υ + f |
(при D ≥ 200 м). |
(16.2) |
Примечание: сущность поправки f рассмотрена далее на примере геометрического нивелирования.
Пять вариантов тригонометрического нивелирования
Рассмотрим пять возможных вариантов тригонометрического нивелирования для расстояний D < 200 м, когда f ≈ 0.
1. Если непосредственно измерено наклонное расстояние D = АВ = JW свето-
дальномером или лентой (см. рис. 16.1), |
тогда в |
треугольнике JWЕ неполное |
превышение равно h' = D sin ν и формула (16.1) получает вид |
||
h = D sin ν + i – |
υ. |
(16.3) |
2. Если известно горизонтальное проложение АВ' = JЕ = d, то
h' = d tg ν и h = d tg ν + i – υ. |
(16.4) |
3. Если наклонное расстояние D измерено нитяным дальномером теодолита, то горизонтальное проложение равно d = D cos2ν. Подставив эту зависимость в выражение (16.4), получим
h' = D cos2ν · tg ν = (1/2)D sin 2ν
и формулу тахеометрического нивелирования
h = (1/2)D sin 2ν + i – υ. |
(16.5) |
4. Если при измерении углов наклона ν визировать на рейку в точку W, отмеченную над ее пяткой на высоте прибора i, то в формулах (16.3), (6.14) и (16.5) слагаемые i = υ (тогда i – υ = 0) и искомое полное превышение будет равно:
h = D sin ν; h = d tg ν; h = (1/2)D sin 2ν. (16.6)
По формулам (16.3) – (16.6) превышение h' вычисляют при помощи инженерных калькуляторов или компьютера. Для определения h' в формуле (16.5) служат также тахеометрические таблицы.
При известной высоте (отметке) НА точки А высоту точки В вычисляют по формуле (см. рис. 16. 1)
НВ = НА + h. |
(16.7) |
Точность тригонометрического нивелирования зависит от погрешностей: D – измерения расстояний; Δν – измерения углов наклона, i – измерения высоты прибора; Δυ – определения высоты наведения. В случае тахеометрической съемки при
помощи теодолитов Т30 |
погрешности измерений примем: D = 0,3 м; Δν = 0,5'; |
i = Δυ = 0,5 см, тогда |
при расстоянии D = 100 м и углах наклона ν < 5° погреш- |
ность величины h' приблизительно равна m h ≈ 1,5 см, а общая погрешность превышения m2h = m2 h + + m2 i + m2Δυ, откуда mh = 1,7 см. При углах наклона ν > 5° погрешность определяемых превышений возрастает.
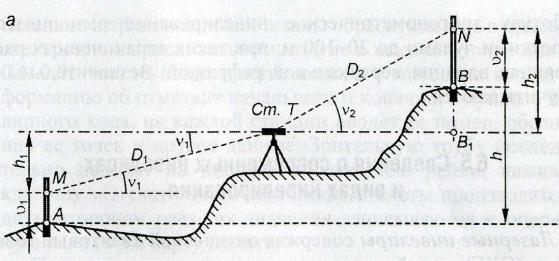
5. Тригонометрическое нивелирование без определения высоты прибора (рис. 16.2) характеризуется повышенной точностью за счет устранения соответствующей
погрешности |
i. На станции Ст. Т тахеометром измеряют расстояния D1 = ТМ и |
|||
D2 = ТN, углы наклона ν1 и ν 2, при этом известны высоты υ1 |
и υ2 визирных целей, |
|||
поставленных на пункты А и В. |
Превышение между точками |
А и В вычисляют |
||
по формуле |
|
|
|
|
h = |
υ1 + h1 + h2 – υ2 = |
υ1 + D1 sin ν1 + D2 sin ν2 – |
υ2. |
(16.8) |
Рис. 16.2. Тригонометрическое нивелирование без определения высоты прибора
16.2. Геометрическое нивелирование, применяемые приборы, их поверки
Геометрическое нивелирование выполняется по схеме рис. 16.3, а при помощи геодезического прибора (нивелира J ) с горизонтальным лучом визирования и нивелирных реек 1 и 2 (прямолинейных мер длины со специальными линейными шкалами), которые ставят вертикально на нивелируемые точки А и В.
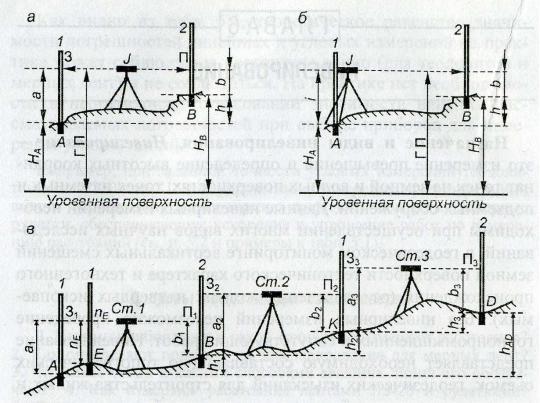
При нивелировании способом из середины нивелир устанавливают на равных расстояниях от точек А и В (см. рис. 16.3, а), на которые ставят нивелирные рейки. Визируют зрительной трубой на шкалу рейки 1 и берут отсчет а, равный высоте визирного луча над точкой А, а по шкале рейки 2 – отсчет b, равный высоте визирного луча над точкой В. Превышение точки В над точкой А – это расстояние h между уровенными поверхностями, проходящими через точки А и В, превышение равно разности отсчетов по рейкам, т.е.
h = а – b. |
(16.1) |
Рис. 16,3. Сущность и способы геометрического нивелирования:
а – из середины; б – вперед; в – нивелирный ход; А, В, К, D – связующие точки; Е – промежуточная точка на станции Ст.1
При нивелировании вперед (рис. 16.3, б) нивелир устанавливают так, чтобы окуляр зрительной трубы прилегал к рейке 1, поставленной вертикально на точку А. Отсчет i по шкале рейки относительно центра окуляра называется высотой прибора над точкой А. Затем визируют на рейку 2, поставленную отвесно на точку В, берут отсчет b и вычисляют превышение
h = i – b. |
(16.2) |
П р и м е ч а н и е. Высоту прибора, у которого зрительная труба обладает перископичностью (т.е. визирный луч в окуляре и в объективе не находятся на одной высоте), определяют относительно объектива так: нивелир ставят в 2-4-х метрах от рейки 1, на нее наводят зрительную трубу и отсчитывают высоту прибора.
Нивелирный ход применяют для последовательного измерения превышения hАD между точками А и D (рис. 6.3, в), разделенными значительным расстоянием или превышением. Нивелируют способом из середины: прибор последовательно устанавливают на станциях Ст. 1, Ст. 2, Ст. 3, которые выбирают на равных расстояниях от задней и передней по ходу точек А и В, В и К, К и D. Искомое превышение
hАD = h1 + h2 + h3 = (а1 – b1) + (а2 – b2) + (а3 – b3) = ∑аi – ∑bi . |
(16.3) |
На каждой станции нивелирного хода различают заднюю и переднюю по ходу связующие точки (В, К,…), между которыми последовательно измеряют превышения. Отсчеты по задней и передней рейкам обозначают символами З и П, при этом превышение hi = (З i – П i) и формулу (16.3) представляют в такой записи:
hАD = h1 + h2 + h3 = (З1 – П1) + (З2 – П2) + (З3 – П3) = ∑Зi – ∑Пi . |
(16.4) |
Вычисление отметок. Если известна высота (отметка) НА точки А над исходной уровенной поверхностью (см. рис. 6.1, а), то высота (отметка) точки В
НВ = НА + h. |
(16.5) |
Высота визирной оси нивелира над исходной уровенной поверхностью называется горизонтом прибора (ГП). Согласно рис. 16.1, а горизонт прибора можно вычислить относительно точек А и В и определить его среднее значение:
ГП' = НА + а = НА + З; ГП" = НВ + b = НВ + П. |
|
ГП = (ГП' + ГП") / 2 . |
(16.6) |
Оносительно среднего значения горизонта прибора данной станции вычисляют отметку каждой точки N, на которую ставили рейку и по горизонтальному лучу брали по ней отсчет nj :
Н j = ГП – nj , |
(16.7) |
например на рис. 16.3, а НА = ГП – а; НВ = ГП – b; или согласно рис. 16.3, в на станции Ст. 1 отметка промежуточной точки Е равна НЕ = ГП1 – nЕ, где nЕ – отсчет по рейке на точке Е.
Влияние кривизны Земли и вертикальной рефракции на результаты ни-
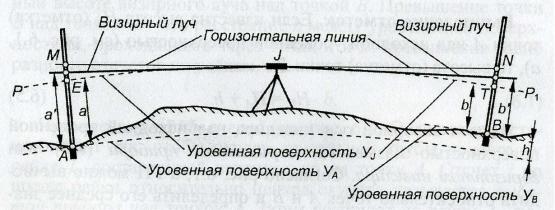
велирования. Формулы (16.1) и (16.2) получены без учета вертикальной кривизны уровенных поверхностей и визирного луча. В приземных слоях воздушная среда обладает неоднородными по вертикали температурой и плотностью и, следовательно, переменным коэффициентом преломления световых лучей. Лучи получают траекторию, которая называется рефракционной кривой. Когда температура земной поверхности выше, чем воздуха, рефракционные кривые JР и JR (рис. 16.4), т. е. визирные лучи отклоняются от горизонтальной линии МJN в сторону земной поверхности и по рейкам, поставленным на точки А и В, получаются отсчеты а' и b'.
Поправки в отсчеты на рефракцию обозначим Ма' = ra и Nb' = rb .
Визирные лучи Jа' и Jb' не совпадают также с уровенной поверхностью визирной оси нивелира УJ = РJР1. Следовательно отсчеты а' и b' по рейкам следует ис-
править поправками на кривизну Земли. Такие поправки равны МЕ = kа и NT = kb .
При проецировании визирных лучей на уровенную поверхность нивелира УJ вычисляют исправленные отсчеты а = АЕ и b = ВТ, для этого в фактические отчеты
а' и b' вводят совместную поправку f на кривизну Земли |
и рефракцию: f = k – r , |
тогда а = а' + fа и b = b' + fb . |
|
Величина f вычисляется по эмпирической формуле |
|
f = 0,42 d 2/ R , |
(16.8) |
где d – расстояние от прибора до рейки; R – средний радиус Земли.
При d = 50, 100, 150, 200, 300 и 1000 м поправка f соответственно равна 0,16;
0,7; 1,5; 2,6; 6 и 67 мм.
Рис. 16.4. Влияние кривизны Земли и рефракции на результаты нивелирования:
АР = а'; ВQ = b' – фактические отсчеты по рейкам А и В; АЕ = а; ВТ = b ‒ отсчеты относительно уровенной поверхности J нивелира
Если расстояния от нивелира до реек одинаковы, то принимается, что рассматриваемые поправки тоже одинаковы, т. е. fа = fb, тогда
h = а – b = (а' + fа ) – ( b' + fb) = а' – b', |
(16.9) |
т. е. фактор кривизны Земли и рефракции практически компенсируется и не влияет на превышение, измеренное способом из середины.
При нивелировании способом вперед фактор рефракции и кривизны Земли влияет на величину превышения
h = i – ( b' + fb) = (i – b' ) – fb , |
(16.10) |
но поправка f учитывается в зависимости от требуемой точности нивелирования.
Учет вертикальной рефракции и кривизны Земли
в инженерно-геодезических работах
При развитии высотных сетей для топографических съемок с точностью нивелирования III и IV класса и технического, при инженерно-геодезических работах по обеспечению монтажа строительных конструкций гражданских и промышленных зданий и сооружений факторы рефракции и кривизны Земли не учитываются по причине их пренебрежимо малых значений (f ≤ 1,5 мм) на расстояниях от ни-
велира до рейки, меньших 120‒150 м (см. формулу 16.8).
