Белорусский национальный технический универстет

Реферат по теме: “Вычеты”

Выполнил: Преподователь:

БНТУ 2013

ВЫЧЕТ

аналитической функции f(z) одного комплексного переменного в конечной изолированной особой точке аоднозначного характера - коэффициент  при  в разложении Лорана функции f(z) (см. Лорана ряд).в окрестности точки а, или равный ему интеграл 

где  - окружность достаточно малого радиуса с центром в точке а. В. обозначается  (либо Выч. ).

Теория вычетов опирается на Коши интегральную теорему. Основной в теории В. является следующая теорема о вычетах. Пусть /(z) - однозначная аналитич. функция всюду в односвяз-ной области G, кроме изолированных особых точек; тогда интеграл от f(z) по любой простой замкнутой спрямляемой кривой g, лежащей в области G и не проходящей через особые точки функции f(z), вычисляется но формуле 

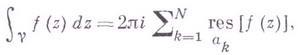
где  - особые точки функции , попавшие внутрь .

Вычет функции в бесконечно удаленной точке  для функции , однозначной и аналитической в окрестности этой точки, определяется формулой 

где - окружность достаточно большого радиуса, ориентированная по часовой стрелке, а - коэффициент при  в разложении Лорана функции  в окрестности этой точки.

Из теоремы о В. вытекает теорема о полной сумме вычетов: если f(z)- однозначная аналитич. функция в расширенной комплексной плоскости, кроме конечного числа особых точек, то сумма всех В. функции , включая В. в бесконечно удаленной точке, равна нулю.

Таким образом, вычисление интегралов от аналитич. функций по замкнутым кривым (контурных интегралов) сводится к вычислению В., к-рые находятся особенно просто в случае конечных полюсов. Пусть  - полюс порядка тфункции , тогда 

При m=1 (простой полюс) эта формула принимает вид 

если  регулярны в окрестности точки а, причем для  точка аесть простой нуль, то

 .

Применение теоремы о В. к логарифмич. производной приводит к важной теореме о логарифмическом вычете: если функция  мероморфна в односвязной области G, а простая замкнутая кривая  лежит в Gи не проходит через нули и полюсы функции , то 

где N - число нулей, Р - число полюсов функции  внутри  с учетом их кратностей. Выражение в левой части этой формулы наз. логарифмическим вычетом функции относительно кривой  (см. также Аргумента принцип).

В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как 

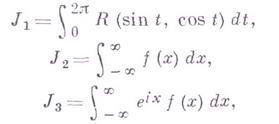
где  -рациональная функция от  непрерывная при - непрерывная функция при  где  - мнимая часть z, и аналитическая при  кроме конечного числа особых точек. При этом  подстановкой  сводится к контурному интегралу 

т. е. к вычислению В.;

если 

если f (z) удовлетворяет условиям Жордана леммы.

В. находят многочисленные и важные применения в вопросах аналитич. родолжения, разложения мероморфных функций на простейшие дроби, суммирования степенных рядов, асимптотич. оценок и во многих др. вопросах анализа и его приложений (см. |1] - [4]).

Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825 - 29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме В. двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом  и др.

На римановой поверхности рассматриваются В. не аналитич. функций, а аналитических дифференциалов (см. [5]). Вычет аналитического дифференциала  в окрестности его изолированной особой точки определяется как коэффициент  при  в разложении Лорана функции  где  - униформизирующий параметр в окрестности этой точки. При этом интеграл от dZ но любой замкнутой кривой на римановой поверхности выражается через В. дифференциала dZ и через его циклические периоды (интегралы от dZ по каноническим разрезам]. На рпмановы поверхности распространяется теорема о полной сумме В.: сумма всех В. мероморфного дифференциала на компактной римановой поверхности равна нулю.

Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши - Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории В. функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие В. на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные В. для обоснования двумерного аналога Лагранжа ряда.

ОСОБЫЕ ТОЧКИ И ИХ КЛАССИФИКАЦИЯ

Точка аС_z называется изолированной особой точкой однозначного характера функции f (z), если f (z) аналитическая и однозначная (регулярная) в кольце {z:0<|z–a|< }, а в самой точке а не определена.

Бесконечно удаленная точка называется изолированной особой точкой однозначного характера функции f (z), если f (z) регулярна в некоторой окрестности {R<|z|<} точки z= и функция 

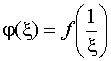
имеет в точке  =0 изолированную особую точку однозначного характера.

В зависимости от поведения функции f (z) вблизи точки а различают следующие три типа особых точек.

Изолированная особая точка а функции f (z) называется

а) устранимой особой точкой, если существует конечный предел

б) полюсом, если

в) существенно особой точкой, если

не существует.

Заметим, что типы особых точек z= функции f (z) и =0 функции совпадают, ибо

Пусть функция f (z) регулярна в точке а (и, следовательно, в некоторой окрестности этой точки). Число т, т1, называется кратностью(или порядком) нуля функции f (z) в точке а, если выполнены условия

f (a)=f  (a)=…=f ^(m-1)(a)=0,

f ^(m)(a) 0.

При т=1 точка а называется простым нулем функции f (z), при m>1-кратным.

Порядком (или кратностью) полюса функции g(z) в точке а называется кратность нуля в точке а регулярной функции

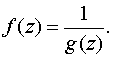
Если а – простой нуль f (z), то точка а называется простым полюсом функции g(z).

Замечание.

Вообще, если

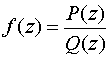, где P(z) и Q(z) – полиномы, не имеющие общих корней, то корни полинома Q(z) (и только они) являются полюсами функцииf (z).

Порядок полюса f (z) совпадает с кратностью соответствующих корней полинома Q(z).

Точка z= называется нулем кратности m1 для функции f (z), регулярной в этой точке, если функция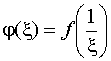 

имеет нуль кратности т в точке  =0.

Если z=а – изолированная особая точка однозначного характера для функции f (z), то f (z) регулярна в некотором кольце {z: 0<|z-a|<r} и ее можно разложить в ряд Лорана, сходящийся в этом кольце,

.

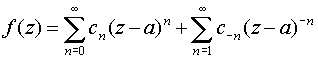Тип изолированной особой точки однозначного характера определяется видом лорановского разложения функции в проколотой окрестности этой точки.

1. Для того чтобы точка а была устранимой особой точкой функции f (z), необходимо и достаточно, чтобы лорановское разложение этой функции в окрестности точки а не содержало главной части.

2. Для того чтобы точка а была полюсом функции f (z), необходимо и достаточно, чтобы главная часть лорановского разложения функцииf (z) в окрестности этой точки содержала лишь конечное число членов (причем полюсом порядка т 1, если главная часть имеет вид

, где с_т0.

3. Точка а тогда и только тогда является существенно особой, когда главная часть лорановского разложения функции f (z) в окрестности этой точки содержит бесконечно много отличных от нуля членов.

Разложение функции f (z) в окрестности бесконечно удаленной точки в ряд Лорана имеет вид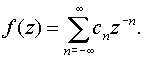 

Здесь роль главной части играют члены с положительными степенями z, а члены с отрицательными степенями образуют правильную часть.

Опираясь на приведенные критерии типа особой точки и определение вычета в точке z=, рекомендуем читателю сформулировать соответствующие утверждения для точки z=.

Основная теорема теории вычетов

Если  аналитична в некоторой замкнутой односвязной области , за вычетом конечного числа особых точек , из которых ни одна не принадлежит граничному контуру , то справедлива следующая формула:

, где  — вычет  в точке .

Для использования теоремы в вычислении вещественных интегралов нужно продолжить интегрируемую функцию на комплексную плоскость и найти ее вычеты, что обычно довольно просто сделать. После этого нужно замкнуть контур интегрирования, добавив к вещественному отрезку полуокружность, лежащую в верхней или нижней комплексной полуплоскости. После этого интеграл по этому контуру можно вычислить, используя основную теорему о вычетах. Зачастую интеграл по полуокружности можно устремить к 0, выбрав ее правильным образом, после чего контурный интеграл станет равен вещественному.

Пример

Интеграл

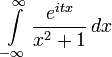
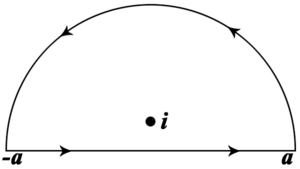
Контур интегрирования.

возникает в теории вероятностей при расчете характеристической функции распределения Коши и не поддается вычислению обычными методами. Вычислим его через интеграл по контуру , указанному на рисунке (). Интеграл равен

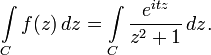
Так как  — целая функция (нет сингулярностей на комплексной плоскости), то функция имеет сингулярности лишь в точках, где . Т.к. , это возможно лишь при  или . В пределах контура лежит лишь одна из этих точек.

Вычет  в  равен

Тогда, по основной теореме о вычетах:

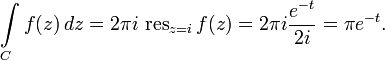
Контур  можно разбить на прямую часть и кривую дугу, так что

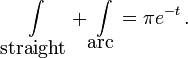
Поэтому

Можно показать, что при :

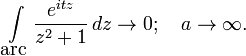
Поэтому, если , то

Аналогичным образом, для дуги, обхватывающей точку  вместо , можно показать, что при :

В итоге получаем:

(При  интеграл вычислим обычными методами анализа и равен )