2) Статистическое имитационное моделирование

Статистическое имитационное моделирование основывается на генерации случайных величин, имитации функционирования системы и статистической обработке результатов моделирования. Методом моделирования может быть исследована СМО любой степени сложности.

Для проведения моделирования могут использоваться как универсальные языки программирования так и проблемно-ориентированные - GPSS, SIMULA и др.

Параметры функционирования системы оцениваются при моделировании по результатам многократного обслуживания требований (многократных испытаний). При имитации работы системы случайные величины (длительность обслуживания в каналах, интервалы между поступлениями требований, время возврата требований в систему, моменты возникновения отказов каналов и их длительность и др.) получают генерацией по ранее приведенным алгоритмам в зависимости от вида распределения (закон, усечение, смещение).

Число обслуживаний (опытов) необходимо принимать таким, чтобы обеспечить оценку интересующих параметров с заданной точностью при принятой доверительной вероятности.

Таким образом, определение числа опытов производится по аналогии с расчетом размера выборки для исследования случайных величин. При этом это число рекомендуется определять в ходе моделирования на основе оценки точности рассчитываемых параметров.

Алгоритмы моделирования ранее рассмотренных систем массового обслуживания приведены на рисунках 2.18 и 2.19. Число моделируемых обслуживаний определяется на основе формулы для нормального закона распределения, а в качестве интересующего показателя принята средняя продолжительность ожидания требованием начала обслуживания. Отноcительная точность оценивания задана равной  с односторонней доверительной вероятностью = 0.95 (квантиль равна 1.645).

Структура алгоритмов следующая:

блок 2– ввод и вывод на принтер исходных данных;

блоки 3-6 – формирование начальных условий моделирования;

блоки 7-10 – поиск канала (источника) с минимальным значением момента времени освобождения от предыдущего обслуживания (прибытия на обслуживание);

блоки 11-18– имитация обслуживания требований и накопление сумм длительностейвремени простоев и обслуживания;

блоки 19-21– принятие решения об окончании моделирования или его продолжении;

блок 22 – наращивание номера опыта (испытания);

блоки 23-24 – вычисление средних значений параметров и вывод их на монитор (принтер).

Оценка адекватности уравнения регрессии данным эксперимента

Для проверки существенности коэффициента множественной корреляции и таким образом оценивания согласованности уравнения регрессии с экспериментальными данными используется статистика критерия Фишера

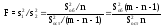или

,

где и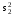– соответственно объясненная и остаточная дисперсия для зависимого параметра.

Чтобы не было оснований отвергнуть гипотезу, что экспериментальные данные согласуются с полученным уравнением регрессии, рассчитанная статистика критерия Фишера должна быть больше табличного значения (F > F_т). Табличное значение F_т определяется в зависимости от уровня значимости γ и числа степеней свободы k₁ и k₂ :

k₁ = n ;

k₂= m - n- 1 .

Уровень значимости (вероятность) рекомендуется принимать 0.01 – 0.05 (чем меньше, тем жестче требования к адекватности модели).

Если F<F_т, то считается, что уравнение регрессии не согласуется с экспериментальными данными.

Оценивание параметров теоретического закона распределения.

Для некоторых законов распределения ниже приведены вид функции плотности вероятности и функции распределения, а также зависимости для вычисления значений параметров.

Нормальный закон распределения

Функция плотности вероятности имеет вид

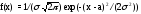
где а и – параметры закона распределения;= 3.1415... .

Функция распределения

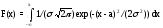
Точечные оценки параметров нормального закона распределения равны: а = x_м,=S.

Логарифмически нормальный закон распределения

Функция плотности вероятности 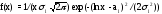, x>0.

Функция распределения .

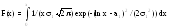Логарифмически-нормальный закон можно описать функцией плотности вероятности нормального распределения, если вместо значений хиспользовать их логарифмы.

Точечные оценки параметров закона распределения:

;

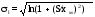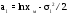
Экспоненциальный закон распределения

Функция плотности вероятности

, x0;

Функция распределения

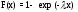, x0

Точечная оценка параметра закона распределения = 1/x_м.

Закон равномерной плотности

,;

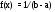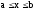Функция распределения

,.

Точечная оценка параметра закона распределения

;

.

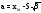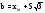Закон распределения Релея

Функция плотности вероятности

, x0;

Функция распределения

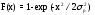, x0;

Точечная оценка параметра закона распределения

.

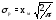Закон распределения Эрланга (гамма-распределение)

Функция плотности вероятности

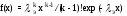, x0;

Функция распределения

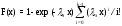, x0;

Точечная оценка параметров закона распределения:

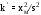и по k' принимается k как ближайшее целое (k=1, 2, 3,...);.

Закон распределения Вейбулла

Функция плотности вероятности

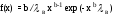, x0;

функция распределения

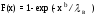, x0;

Точечная оценка параметров закона распределения

;

.

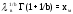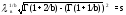Загрузка каналов и их возможные приоритеты в системах массового обслуживания

В системах с приоритетами требований различают относительный приоритет (без прерывания обслуживания), когда при поступлении требования с более высоким приоритетом оно принимается на обслуживание после окончания ранее начавшегося обслуживания требования с меньшим приоритетом, и абсолютный приоритет, когда канал освобождается немедленно для обслуживания поступившего требования с более высоким приоритетом.

Шкала приоритета может быть построена исходя из каких-то внешних относительно системы обслуживания критериев или на показателях, связанных с работой самой системы обслуживания. Практическое значение имеют следующие типы приоритетов:

разделение входящих требований по категориям приоритетности в зависимости от их источников;

приоритет у требований с наименьшим временем обслуживания. Эффективность данного приоритета может быть показана на следующем примере. Поступили последовательно два требования с длительностью обслуживания соответственно 6,0 и 1,0 ч. При приеме их на обслуживание освободившимся каналом в порядке поступления простой составит для 1-го требования 6,0 ч и для второго 6,0+1,0 = 7,0 ч или суммарно для двух требований 13,0 ч. Если дать приоритет второму требованию и его принять на обслуживание первым, то его простой составит 1,0 ч и простой другого– 1,0+6,0 = 7,0 ч или суммарно для двух требований 8,0 ч. Выигрыш от назначенного приоритета составит 5,0ч (13-8) сокращения простоев требований в системе;

приоритет у требований с минимальным отношением времени обслуживания к мощности (производительности) источника требования, например, к грузоподъемности автомобиля.

Механизм обслуживания характеризуется параметрами отдельных каналов обслуживания, пропускной способностью системы в целом и другими данными об обслуживании требований. Пропускная способность системы определяется числом каналов (аппаратов) и производительностью каждого из них.

Определение доверительных интервалов случайных величин

Интервальная оценка параметра распределения случайной величины определяется тем, что с вероятностью 

abs(P – P_м) ≤,

где P – точное (истинное) значение параметра;

P_м – оценка параметра по выборке;

 – точность (ошибка) оценивания параметра Р.

Наиболее часто принимают  от 0.8 до 0.99.

Доверительный интервал параметра [P_м–, P_м+] – это интервал, в который попадает значение параметра с вероятностью . Например, на этой основе находится требуемый размер выборки случайной величины, который обеспечивает оценку математического ожидания при точности  с вероятностью . Вид связи определяется законом распределения случайной величины.

Вероятность попадания случайной величины в заданный интервал [Х₁, Х₂] определяется приращением интегральной функции распределения на рассматриваемом интервале F(Х₂)–F(Х₁). Исходя из этого, при известной функции распределения можно найти ожидаемое гарантированное минимальное Х_гн (x≥ Х_гн) или максимальное значение Х_гв (x≤ Х_гв) случайной величины с заданной вероятностью  (рисунок 2.15). Первое из них является тем значением, больше которого случайная величина будет с вероятностью , а второе – что случайная величина с вероятностью  меньше этого значения. Гарантированное минимальное значение Х_гн с вероятностью  обеспечивается при F(x)= 1- и максимальное Х_гв при F(x)=. Таким образом, значения Х_гн и Х_гв находятся по выражениям:

Х_гн = F^-1 (1-);

Х_гв = F^-1 ().

Пример. Случайная величина имеет экспоненциальное распределение с функцией .

Требуется найти значения Х_гн и Х_гв, для которых случайная величина х с вероятностью =0.95 соответственно больше Х_гн и меньше Х_гв.

Исходя из того, что F^-1 (α) = -1/ ln(1- α) (см.вывод ранее) и α = 1- = 0.05 получаем

Х_гн = -1/ ln(1- α) = -1/0.01 ln(1-0.05)=-100 (-.0513)=5.13.

Для Х_гв α =  = 0.95 аналогично имеем

Х_гв = -1/ ln(1- α) = -1/0.01 ln(1-0.95)=-100 (-2.996)=299.6.

Для нормального закона распределения значения Х_гн и Х_гв могут быть рассчитаны по формулам

Х_гн = х_м + s U_1- = х_м - s U_ ;

Х_гв = x_м + s U_ ,

где x_м – математическое ожидание случайной величины; s – среднеквадратическое отклонение случайной величины; U_ – односторонняя квантиль нормального закона распределения при вероятности .

1.0

F(x)

0.80

0.60



0.40

0.20

1-

x_гн x_гв x

Рисунок 2.15 – Графическая интрепретация определения Х_гн и Х_гв

Описание потоков требований на обслуживание

Входящий поток представляет собой последовательность требований (заявок), прибывающих в систему обслуживания, и характеризуется частотой поступления требований в единицу времени (интенсивностью) и законом распределения интенсивности потока. Входящий поток может быть описан также интервалами времени между моментами поступления требований и законом распределения этих интервалов.

Требования в потоке могут поступать по одному (ординарные потоки) или группами (неординарные потоки).

Свойство ординарности потока заключается в том, что в любой момент времени может поступить только одно требование. Иными словами, свойство заключается в том, что вероятность поступления больше одного требования за малый промежуток времени есть бесконечно малая величина.

В случае группового поступления требований задается интенсивность поступления групп требований и закон ее распределения, а также размер групп и закон их распределения.

Интенсивность поступления требований может изменяться во времени (нестационарные потоки) или зависит только от единицы времени, принятой для определения интенсивности (стационарные потоки). Поток называется стационарным, если вероятность появления n требований за промежуток времени (t₀, t₀+Δt) не зависит от t₀, а зависит только от Δt.

В нестационарном потоке интенсивность изменяется во времени по непериодической или периодической закономерности (например, процессы сезонного характера), а также может иметь периоды, соответствующие частичной или полной задержке потока.

В зависимости от того, имеется ли связь между числом требований, поступивших в систему до и после некоторого момента времени, поток бывает с последействием или с отсутствием последействия.

Ординарный, стационарный поток требований с отсутствием последействия является простейшим.

Критерии согласия Пирсона и Романовского