Статика

1.Аксиомы статики. Основные задачи статики.

АКСИОМЫ СТАТИКИ: I Если на матер тело действуют 2 силы, тело может сохранять состояние покоя, если силы = по модулю, дейст-ют вдоль одной прямой в противоположные стороны

II Действие данной с.с на тело не измен если + к ней или – от неё уравновешенную сис-му сил.

Следствие из 1 и 2 акс: Не изменяя действия данной силы на тело т приложения её можно переносить вдоль линии действия куда угодно.

III Если на матер-ое тело действуют 2 силы, приложенные в одной точке, они имеют равнодействующую, изображаемую диагональю параллелограмма, постр на силах как на сторонах.

IV Всякое действие одного мат тела на др вызывает = по величине , но противопол по направлению противодействие.

Основные задачи статики:

1.Приведение данной системы сил к простейшему виду.

2.Установление условий равновесия данной системы сил.

2.Связи и их реакции.

СВЯЗЬ. РЕАКЦИИ СВЯЗЕЙ. Свободным наз тело, не связанное с др телами, кот из данного положения можно придать любое перемещение в пространстве. Несвободное – тело, перемещению кот-го в пространстве препятствуют др тела.

Основные виды связей.

1 Гладкая пов-сть, плоскость. Полная реакция всегда направлена по нормали соприкасающимся пов-стям.

2 Шарнирно-подв опора. Полная реакция всегда направлена по нормали к пов-сти, по кот перемещ катки. 1 связь – верт; 2 ст св – вращ+гор;

3 Шарнирно неподв опора. 1 связь – верт+гор; 1 ст св – вращ

ПРАВИЛО: Полная реакция произвольным образом расположена в плоскости. Её надо разложить на верт-ую и гориз-ую составляющие.

4 Жёсткое защемление. 3 связи.

5. Стержень. Полная реакция в стержне всегда направлен вдоль оси стержня.

3.Как определить равнодействующую сходящихся сил?

1. Построение параллелограмма

равнодействующая двух сил, приложенных к одной точке, приложена в этой точке и равна диагонали параллелограмма, построенного на данных силах

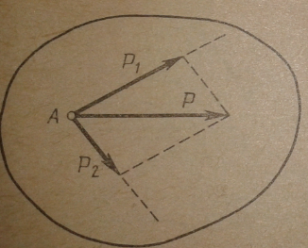
2. Силовой треугольник.

Направление равнодействующей силы R по контуру силового треугольника противоположно направлению обхода контура треугольника, определяемому слагаемыми силами

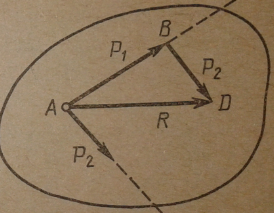
4.Теорема о равновесии трёх непараллельных сил.

Если твердое тело находится в равновесии под действием трёх непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

5.Пара сил. Её характеристики.

Пара сил – система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твёрдое тело.

Плоскость действия пары – плоскость, проходящая через линии действия пары сил.

Плечо пары – расстояния между линиями действия пары сил. Момент пары сил – называется вектор m(или M) модуль которого равен произведению модуля одной из сил пары на её плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящийся повернуть тело против хода часовой стрелки.

6.Можно ли уравновесить пару сил? Если да, то, каким образом?

Нельзя, т.к. пара сил не имеет равнодействующих. И они направлены не по одной прямой.

7.Векторное и аналитическое выражение момента силы относительно точки.

Момент силы относительно точки в пространстве определим как век­торную вели­чину в виде векторного произведения , где- радиус-вектор, прове­дённый из точки в точку приложениясилы

8.Как определить момент силы относительно оси ?

Момент силы относительно оси называется скалярная величина равная моменту проекции этой силы на плоскость перпендикулярной оси взятой относительно точки пересечения оси с плоскостью. Mz(F)=mz(F xy)=m0(Fx,y)=+-Fxyh

9.можно силу перенести параллельно самой себе? Если да, то каким образом?

Силу F не изменяя её действия на твёрдое тело можно перенести из точки её

приложения A в любой цент приведения O приложив при этом к телу с моментом M геометрически равный M₀ этой силы относительно центра приведения.

10.Условия равновесия различных систем сил.

Условия равновесия произвольной системы сил в пространстве. Необходимыми и достаточными условиями равновесия произвольной пространственной системы сил, приложенных к твердому телу, являются обращение в нуль ее главного вектора и главного момента относительно какой-либо точки пространства

Условия равновесия произвольной пространственной системы сил можно выразить в геометрической форме: многоугольники сил и моментов этих сил должны быть замкнутыми.

Таким образом, произвольная система сил, расположенных в одной плоскости, уравновешивается лишь в том случае, когда алгебраические суммы проекций всех сил на две координатные оси (Ох и Оу) и алгебраическая сумма моментов сил относительно произвольной точки этой плоскости равны нулю

Для равновесия системы параллельных сил в прост­ранстве необходимо и достаточно, чтобы алгебраическая сумма проекций сил на ось, им параллельную, равнялась нулю и алгебраическая сумма моментов сил относительно двух дру­гих координатных осей равнялась нулю

для равновесия параллельных сил, расположенных в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций сил на параллельную им ось и алгебраическая сумма моментов этих сил относительно произвольной точки равнялись нулю