Вопрос 1: перемещение,скорость материальной точки, вычесление пути

Линия, описываемая материальной точкой при её движении в пространстве, называется траекторией. Расстояние между двумя положениями точки, измеренное вдоль траектории называется путем, пройденным телом. (Путь – длина траектории.)

Вектор, соединяющий начальное положение тела с конечным положением, называется вектором перемещения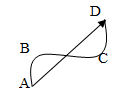

ABCD – траектория

AD - перемещение

Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.

Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор г0 (рис. 3). В течение малого промежутка времени t точка пройдет путь s и получит элементарное (бесконечно малое) перемещение г

РИС 3

Если путь s, пройденный материальной точкой за промежуток времени t₂-t₁, разбить на достаточно малые участки Ds_i, то для каждого i-го участка выполняется условие

Тогда весь путь можно записать в виде суммы

При стремлении всех Dt_i к нулю это приближенное равенство становится точным, то есть

Вопрос 2 нормальное и тангенциальное ускорение

Таким образом, ускорение а есть векторная величина, равная первой производной скорости по времени.

Разложим вектор Dv на две составляющие. Для этого из точки А (рис. 4) по направлению скорости v отложим вектор , по модулю равный v1. Очевидно, что вектор , равный Dv, определяет изменение скорости за время Dt по модулю: Dv = v1 - v. Вторая же составляющая Dvn вектора Dv характеризует изменение скорости за время Dt по направлению.

Тангенциальная составляющая ускорения

т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому Ds можно считать дугой окружности некоторого радиуса г, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует , но так как AB=vDt, то

В пределе при Dt  0 получим v1  v.

Поскольку v1 = v, угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол ADE между v и Dvn стремится к прямому. Следовательно, при Dt  0 векторы Dvn и v оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор Dvn, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением). Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 5):

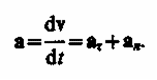
Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения — быстроту изменения скорости по направлению (направлена к центру кривизны траектории).