3 Прямые общего положения. Следы прямой

Прямые общего положенияне параллельны, а соответственно, и не перпендикулярны плоскостям проекцийH,VиW. Поэтому на чертеже их проекции не параллельны и не перпендикулярны осям проекций Х, У иZи искажают натуральную величину этих прямых.

Теорема о принадлежности точки прямой: если точка принадлежит прямой, то на чертеже проекции точки лежат на одноименных проекциях прямой.Следы прямойназываются точки ее пересечения с плоскостями проекций.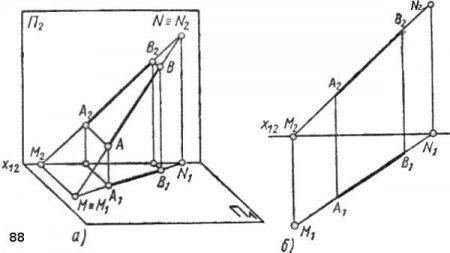

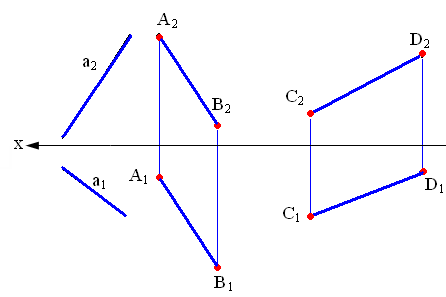
4 Прямые частного положения. Особенности их проекций

Прямые частного положенияпараллельны и перпендикулярны одной или двум плоскостям проекций. По этому признаку их разделяют на две группы: прямые уровня и проецирующие прямые.Прямые уровня– прямые, параллельные одной плоскости проекций: фронтальные – параллельны плоскости проекцийV; горизонтальные – параллельны плоскости проекцийH; профильные – параллельны плоскости проекцийW.

Характерные признаки расположения проекций фронтальной прямой на чертеже: фронтальная проекция расположена к оси проекций Х под углом, который определяет ее наклон к плоскости проекций Н, она определяет натуральную величину прямой; горизонтальная проекция параллельна оси Х; профильная проекция параллельна осиZ;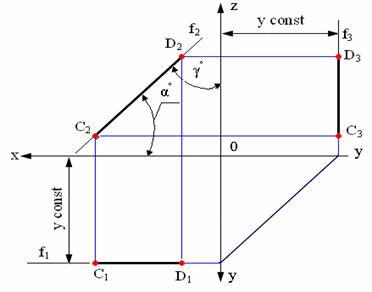

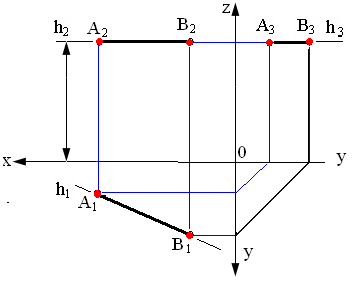
Характерные признаки расположения проекций горизонтальной прямой на чертеже: фронтальная проекция параллельна оси проекций Х; горизонтальная проекция расположена к оси проекций Х под углом, который определяет ее наклон к плоскостиV, она определяет натуральную величину прямой; профильная проекция параллельна оси проекций У;

Характерные признаки расположения проекций профильной прямой на чертеже: фронтальная проекция перпендикулярна оси Х; горизонтальная проекция перпендикулярна оси Х; профильная проекция расположена под углом к плоскости проекцийVи под углом к плоскости проекций Н, она определяет натуральную величину прямой.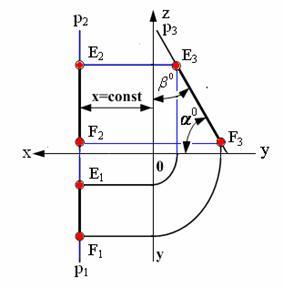

Проецирующие прямые – прямые, перпендикулярные одной плоскости проекций (параллельны двум плоскостям проекций):

Фронтально-проецирующие– перпендикулярны плоскостиV(параллельны плоскостям Н иW); Характерные признаки: фронтальная проекция представляет собой точку; горизонтальная проекция расположена перпендикулярно оси Х, и опр. Натур. Велич. Прямой; профильная проекция располож. Перпендикулярно осиZи также опр. Натур. Велич.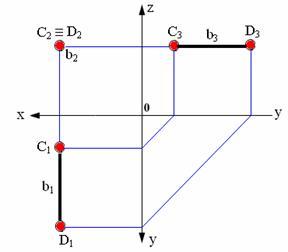

горизонтально-проецирующие– перпендикулярны плоскости проекций Н (параллельны плоскостямVиW); Характерные признаки: фронтальная проекция перпендикулярна оси Х и опр. Натур. Велич.; горизонтальная проекция представляет собой точку; профильная проекция перпендик. Оси У и также опр. Натур. Велич. Прямой.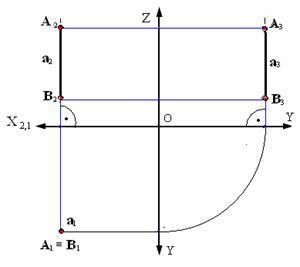

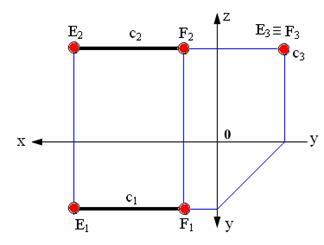
профильно-проецирующие – перпендикулярны плоскостиW. Характерные признаки: фронтальная проекция параллельна оси Х и опр. Натур. Велич. Прямой; горизонтальная проекция параллельна оси Х и также опр. Натур. Велич. Прямой; профильная проекция представляет собой точку.

5 Взаимное расположение прямых. Конкурирующие точки. Теорема о проецировании прямого угла.

Взаимное положение прямых: параллельные прямые– прямые параллельные в пространстве имеют одноименные проекции также параллельные на чертеже;пересекающиеся прямые– прямые пересекающиеся в пространстве, на чертеже проекции точки пересечения прямых лежат на одной линии связи.Скрещивающиеся прямые – это две не параллельные и не пересекающиеся прямые, которые в пространстве скрещиваются. На чертеже их проекции могут накладываться, образуя конкурирующие точки, лежащие на одном проецирующем луче.

Конкурирующие точки – точки лежащие на одном проецирующем луче, точки могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. С их помощью можно определить видимость проекции на чертеже.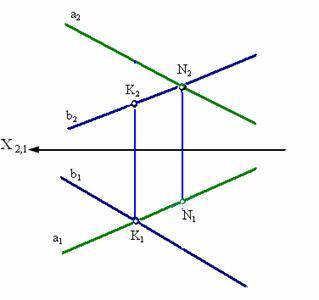

Теорема о проецировании прямого угла: если одна сторона прямого угла параллельна какой-либо плоскости проекций, а вторая сторона ей не перпендикулярна и не параллельна, то на эту плоскость проекций угол проецируется в натуральную величину, т е прямым.