
- •4.Связь напряженности с потенциалом Эл.П.
- •2. Напряженность Эл.П. Принцип суперпозиции.
- •3.Работа электростатического поля. Потенциал.
- •60 Применение теоремы Гаусса к расчету электростатических полей
- •13.Энергия электрических зарядов заряженных проводников и конденсаторов.
- •7 Статическое поле в веществе. Электрический диполь. Поляризованные заряды. Поляризованность
- •20. Закон Ома в классической электронной теории
- •21. Сила Ампера. Вектор магнитной индукции
- •22. Закон Био-Савара-Лапласа
- •23. Магнитное поле прямолинейного проводника с током.
- •24. Определение единицы силы тока-Ампера
- •26.Закон полного тока
- •27. Магнитное поле Тороида и длинного соленоида
- •29. Эффект Холла. Мгд генератор (магнитогидродинамический)
- •28. Сила Лоренца
- •30. Магнитный поток. Теорема Остроградского-Гаусса.
- •31.Контур и виток с током в магнитном поле.
- •65. Пьезоэлектрический и пироэлектрический эффекты.
- •32. Явление электромагнитной индукции. Правило Ленца.
- •33 Фарадеевская и Максвеловская трактовка явления электромагнитной индукции
- •34° Самоиндукция. Индуктивность. Коэффициент взаимной индукции.
- •35° Магнитная энергия тока. Плотность магнитной энергии.
- •Вопрос 36. Магнитное поле в веществе. Намагниченность.
- •Вопрос 38. Типы магнетиков. Диа- и парамагнетики.
- •39. Феромагнетики. Доменная структура. Техническая кривая намагниченности.
- •40. Ток смещения. С-ма ур-ий электродинамики Максвела в интегр. Форме.
- •42. Скорость распространения электромагнитных возмущений. Волновое уравнение.
- •47 Дифракция света
- •49)Дифр.Френеля на угол отверстия.
- •51. Дифракционная решётка.
- •53. Дифракция на пространственной решетке. Формула Вульфа-Брэгга.
- •54. Излучение Вавилова-Черенкова.
- •55. Дисперсия света в области нормальной и аномальной дисперсии.
- •56.Поглащение и рассеивание света
- •57.Поляризация света.Естественная поляризация.Поляр-я при отражении
- •58.Двойное лучепреломление
- •59° Поляроиды и поляризационные призмы.
- •60 Поляризация света. З-н Малюса .
- •61.Искусственная оптическая оспизотропия. Эффект Керра.
- •62.Контактная разность потенциалов. Законы Вольта.
- •63.Явление термоэлектр. Эффект Зеебека.
- •64.Эффекты Пельтье и Томсона.
60 Применение теоремы Гаусса к расчету электростатических полей
Теорема Гаусса совместно с принципом суперпозиции позволяет вычислять поля при симметричном расположении зарядов.
а) поле бесконечной, равномерно заряженной плоскости.
Пусть
плоскость заряжена с поверхностной
плотностью заряда σ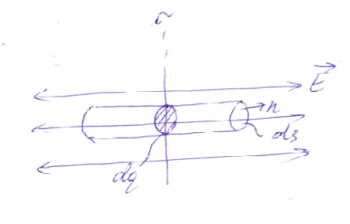
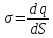
За Гауссовую поверхность возьмем прямой круговой цилиндр с осью перпендикулярной плоскости и основаниям dS . Поток напряженности через боковую поверхность цилиндра равен 0
En=0 ,остается поток через основание цилиндра
dNE=EdS+EdS=2EdS
Заряд внутри dq=σdS
dNE=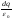 2EdS=
2EdS=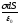
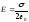
Если в среде:
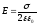
б) Поля двух равномерно заряженных плоскостей. Пусть плоскости заряжены с поверхностной плоскостью заряда σ
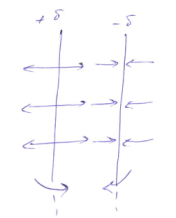
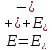
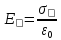 -
внутри
-
внутри
Вне E=0
Среда
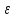 ,
,
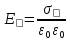
в) Поле заряженной сферы
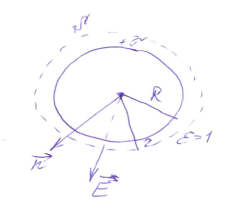
Рассмотрим
заряженную сферу с поверхностной
плотностью заряда
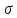
За Гауссовую поверхность возьмем сферу с r.
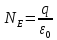
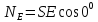
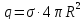
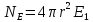
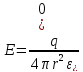
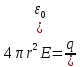
Среда
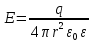
Г)
Поле
заряженного шара. Пусть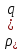 -
объемная плотность электрического
заряда, тогда совершенно аналогично
получаем выражение для напряженности
поля, создаваемого зарядами шара в
точке на расстоянииr
от центра шара.
-
объемная плотность электрического
заряда, тогда совершенно аналогично
получаем выражение для напряженности
поля, создаваемого зарядами шара в
точке на расстоянииr
от центра шара.
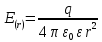
д) Поле заряженной бесконечной нити


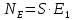
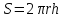
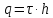
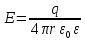
13.Энергия электрических зарядов заряженных проводников и конденсаторов.
![]() W=q1×q2/4πεε0r.
W=q1×q2/4πεε0r.
Рассмотрим теперь заряженный проводник,чтобы увеличить заряд проводника на dq надо переместить этот заряд из бесконечности на проводник и совершить при этом работу, против сил электрического поля проводника:
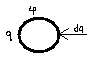 dA=dq(φ-φ∞)
, φ∞=0,
dA=dqφ
, dA=Cφdφ.
Эта работа идет на увеличение энергии
проводника, dA=dW,
dW=Cφdφ,
W=Cφ2/2+const.
dA=dq(φ-φ∞)
, φ∞=0,
dA=dqφ
, dA=Cφdφ.
Эта работа идет на увеличение энергии
проводника, dA=dW,
dW=Cφdφ,
W=Cφ2/2+const.
Рассмотрим энергию заряженного конденсатора, пусть малый заряд dq проходит между обкладками конденсатора тогда работа по перемещению заряда dq/dA=Udq. Т.к. q=CU , dq=CdU , dA=CUdU-это работа по перемещению заряда , W=CU2/2=U2/2C=qu/2.
7 Статическое поле в веществе. Электрический диполь. Поляризованные заряды. Поляризованность
По электропроводности материалы делятся:
Проводники (металлы, электролиты)
Полупроводники (германий, кремний)
Диэлектрики (стекло, вата)
Диэлектрики
проводят электрический ток 1015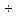 1020
раз хуже чем проводники
1020
раз хуже чем проводники
Молекулы и атомы, диэлектрики в целом электрически нейтральны. Электрические заряды в атомах и молекулах связаны друг с другом и не могут перемещаться по всему объему диэлектрика. Также заряды называются поляризованными, связанными. Заряды, которые могут перемещаться называются свободными (сторонними).
В зависимости от строения молекул различают три типа диэлектриков
1.Неполярные
2.Полярные
3.Кристаллические
Если в отсутствии внешнего электрического поля E=0 ,центры распределения положительных и отрицательных зарядов смещаются в противоположные стороны на малое расстояние по сравнению с размерами молекул.
Такую молекулу рассматривают как упругий диполь.
![]()
Электрический диполь – система двух равных по величине, но противоположные по знаку электрических зарядов, находящихся близко друг к другу по сравнению с расстояниями, на которых рассматривается этот диполь.
Основная характеристика диполя – электрический дипольный момент
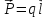
Это произведение положительного заряда на плечо.
Если в отсутствии внешнего электрического поля распределения положительных и отрицательных зарядов молекул не совпадают из-за ассиметричного строения молекулы называется полярной, а диэлектрик –полярным.
Полярным диэлектриком является вода.
При отсутствии внешнего поля дипольные моменты отдельных молекул ориентированы хаотично в силу теплового движения молекул и в целом диэлектрик не имеет дипольного момента.
Во внешнем электрическом поле диполи ориентируются по полу и дипольный момент диэлектрика отмечают 0.
Кристаллические диэлектрики имеют ионное строение, во внешнем поле происходит смещение положительных и отрицательных ионов ,диэлектрики приобретают дипольный момент.
Поляризация диэлектрика:
Во внешнем эл.поле есть переход диэлектрика в такое состояние , когда дипольный момент всего объема отличен от 0.
За
меру поляризации диэлектрика принимают
поляризованность .
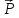 –дипольный
момент единицы объема
–дипольный
момент единицы объема
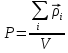
Суммирование происходит по всем дипольным моментам находящимся в объеме V.
Единицы измерения дипольного момента
[p]=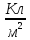
17. Законы Ома И Джоуля-Ленца в диф. форме.
Законы Ома и Джоуля- Ленца в дифференциальной форме
Из Опыта известно что сопротивление R цилиндрического проводника длиною l и площадью поперечного сечения S:
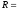 ρ
ρ
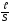 S
S
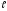


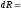 ρ
ρ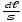 [ρ]=
Ом∙м ρ
= ρ
[ρ]=
Ом∙м ρ
= ρ (1+α)
(1+α)
I=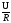 I=
I=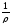 ∙
∙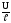 ∙S
│:S
∙S
│:S
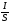 =
=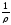 ∙
∙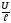
Это эквивалентно выражению ј =σE
ј= σE (над всеми вектора)-это закон Ома в диф.форме
Если напряжённость поля E(с вектором) складывается из E электр. и E стор.
ј
=σ(Eэл+Eстор)
(вектора над всеми кроме σ)

Закон Джоуля-Ленца (1841-1842)
При прохождении заряда q через проводник I=q/t q=It
Тогда совершается работа A=qU=IUt
Если проводник неподвижный и отсуствует хим.реакции, то работа А идёт на увеличение внутренней энергии проводника.
Q=IUt
Чаще в такой форме Q=I2Rt
Если ток переменный I=I(t) dQ=I2 (t)Rt
Q=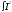 (t)Rdt
(t)Rdt
Получим теперь закон в диф.форме(локальной форме)
Объёмной плотностью тепловой мощности называется тепловая энергия в единице объёма за единицу времени.
ω
=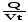
Поскольку Q=IUt то получим
ω
= =
=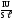 =
јE
=
јE
ω= јE (всё с векторами кроме ω) –закон Джоуля-Ленца в диф.форме
ω=σE2 т.к E=ј/σ
ω=
ρ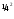
18 Правило Киргоффа расчёта разветвлённых электр.цепей.
Рассмотрим электр. цепь.
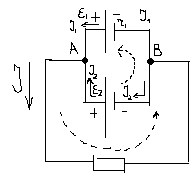
Узлом называется точка в которой сходятся 3 и более проводника.
1 правило киргоффа-
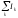 =0
=0
ток
входящий в узел +
ток выходящий - -
узел A: I1-I2-I=0 (1)
узел B:-I1-I2+I=0 (2)
2 правило:
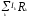 =
=
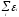
Алгебраическая сумма произведений токов на сопротивления соответствующих участков в цепи равеая алгебраической сумме ЭДС на рассматриваемом контуре.При этом выбирают определённое направление обхода контура.если направление тока совпадает с направлением обхода контура то его считают положительным.
ЭДС считают + если при выбранном направлении ток проходит от – к +
При этом число независимых уравнений получается меньше чем общее число контуров…
r
1
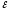 1R1
:
1R1
:
I1r1+IR=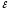 1
(3)
1
(3)
Контур
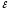 1
r 1
1
r 1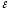 2
r 2 :I1r1-I2r2=
2
r 2 :I1r1-I2r2=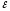 1-
1-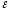 2
(4)
2
(4)
Контур
R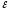 2
r 2 :I2 r2+IR=
2
r 2 :I2 r2+IR=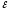 2
(5)
2
(5)
(4)+(5) 3
3
(1) (3) (4) позволяют найти токи I1 I2 I
