2.2. Закономерности движения реальной жидкости в цилиндрической трубе

Пусть имеется жидкость, различные слои которой движутся с различными скоростями (рисунок 1), причем скорости слоев, отстоящих на расстоянии Δy, отличаются на величину Δv. Тогда отношение Δv/Δy показывает, насколько быстро меняется скорость жидкости от одного слоя к другому. Для двух бесконечно близких слоев (Δy0) эта величина записывается в виде dv/dy и представляет собой градиент скорости grad(v) в направлении перпендикулярном скорости движения слоев.

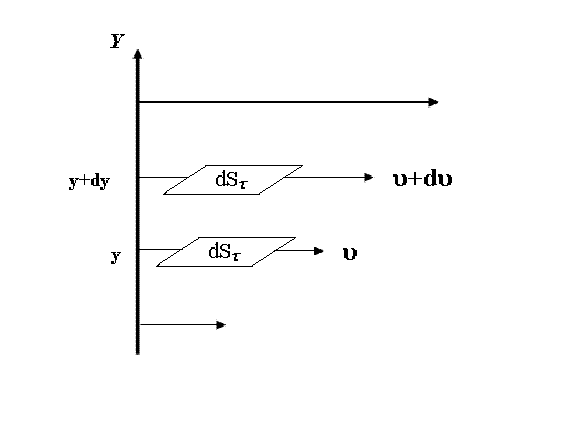
Рис.1. Схематическое изображение слоев.

Ньютон впервые предположил, что сила вязкости или сила внутреннего трения dF_в между двумя слоями жидкости прямо пропорциональна площади их соприкосновения dS_τ, а также градиенту скорости:

. (1)

Коэффициент пропорциональности _, зависящий от природы жидкости и ее температуры, называется коэффициентом вязкости или просто вязкостью. Коэффициент вязкости  измеряется в Па·с.

Рассмотрим более подробно ламинарное течение жидкости по трубе круглого сечения радиуса R длиной l. Если разность давлений ΔP = P₁ – P₂ (P₁ > P₂) на концах трубы поддерживается постоянной, то установится стационарный режим течения, при котором за равные промежутки времени t через любое поперечное сечение трубы S будут протекать равные объемы жидкости V. Особенность течения вязкой жидкости по цилиндрической трубе состоит в том, что внешний слой жидкости, примыкающий к внутренней поверхности трубы, прилипает к ней и остается неподвижным, а скорость каждого из последующих слоев увеличивается по мере приближения к центру трубы. Течение жидкости можно представить в виде движения цилиндрических слоев, параллельных оси трубы. Мысленно выделим произвольную цилиндрическую область жидкости радиуса r и длины l (рисунок 2).

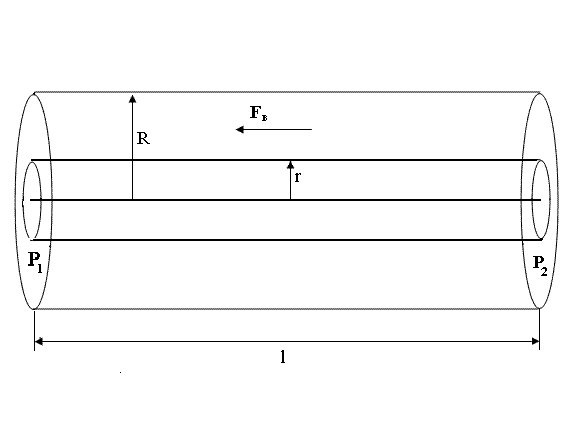
Рис.2. Схематическое изображение цилиндрической области жидкости.

На ее боковую поверхность S_=2rl со стороны внешнего слоя, текущего с другой скоростью, действует, согласно (1), сила вязкости:

. (2)

Кроме того, на основания цилиндра действует сила, связанная с разностью давлений:

. (3)

При стационарном течении жидкости скорость движения жидкости постоянна, поэтому силы, действующие на цилиндрический слой, должны быть равны и противоположны по направлению F_B=F_P, следовательно

. (4)

Выразим из этого уравнения dv и проинтегрируем получившееся выражение для того, чтобы найти скорость:

Пределы определенного интеграла выбраны из условия, что на стенке трубы (т.е. при r = R), скорость v должна обращаться в нуль. В результате получим

. (5)

Таким образом, скорость частиц движущейся жидкости изменяется от максимального значения (на оси трубы) до нуля (на стенках трубы) по параболическому закону (рисунок 3).

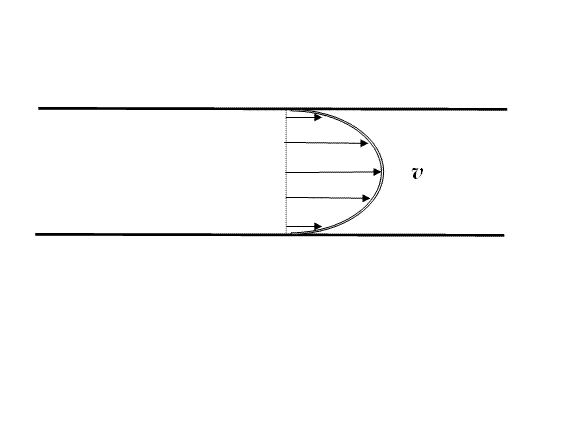
Рис.3. Распределение скоростей слоев жидкости в трубе.

Подсчитаем объем жидкости, протекающей через поперечное сечение трубы за время t. Для этого рассмотрим тонкий цилиндрический слой радиуса r, толщиной dr, текущий с постоянной скоростью v. За время t через кольцевую площадку площадью dS = 2πrdr, которая представляет собой поперечное сечение этого тонкого слоя, протечет объем жидкости – dV =dS vt = 2πrdr vt или, используя формулу (5),

(6)

Объем жидкости V, протекающей за время t через все поперечное сечение трубы S, находится путем интегрирования выражения (6) по r от 0 до R.

(7)

Разделив данное выражение на время t, получим объем жидкости, вытекающий из трубы за единицу времени или расход жидкости Q=V/t, а формула (7) будет иметь вид:

(8)

Формула (8) является количественным выражением закона Пуазейля. Из нее, в частности, следует, что расход жидкости обратно пропорционален длине трубы – l, и прямо пропорционален разности давлений на концах трубы и четвертой степени ее радиуса, то есть, чрезвычайно сильно возрастает с увеличением радиуса трубы.

Если предположить, что все частицы жидкости движутся не с различными скоростями, а с некоторой средней скоростью v_ср, то расход жидкости Q, то

. (9)

Эксперименты показали, что закон Пуазейля оказывается справедливым лишь при относительно небольших скоростях движения жидкости. Осборн Ре΄йнольдс впервые заметил, что при достижении некоторой критической скорости движение жидкости теряет ламинарной характер и становится турбулентным (вихревым), то есть, струйка подкрашенной жидкости быстро расходится по всему сечению трубы в виде вихревых образований. Кроме того, было замечено, что значение критической скорости зависит также от размеров трубки и свойств самой жидкости. Так, например, если одна и та же жидкость течет по трубам различного диаметра, то в более широкой трубе переход от ламинарного течения к турбулентному будет происходить при меньших скоростях движения, чем в узкой. Таким образом, узкая труба оказывает более сильное, упорядочивающее влияние на характер движения жидкости. С другой стороны оказалось, что более вязкая жидкость сохраняет ламинарность течения при относительно более высоких скоростях движения.

Рейнольдс предложил характеризовать течение жидкости безразмерной величиной, названной числом Рейнольдса:

. (10)

Здесь  и  - плотность и вязкость жидкости, v_ср - средняя скорость ее течения, R – радиус трубы.

Экспериментальные исследования показали, что ламинарный режим наблюдается при течениях, которым соответствуют значения чисел Рейнольдса не более ~1000. Переход от ламинарного к турбулентному течению происходит в области значений от 1000 до 2000, а при значениях Re > 2000 течение становится турбулентным.