Параллельное соединение потребителей

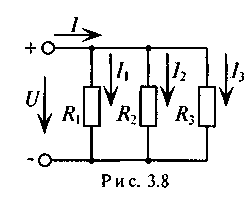
Параллельным соединением участков электрической цепи называ­ют соединение, при котором все участки цепи присоединяются к од­ной паре узлов, т. е. находятся под действием одного и того же на­пряжения (рис. 3.8). Токи параллельно включенных участков об­ратно пропорциональны сопротивлениям этих участков.

При параллельном соединении сопро­тивлений R₁, R₂ и R₃ токи потребителей соответственно равны

Воспользовавшись первым законом Кирхгофа, можно определить ток Iв не-разветвленной части цепи

Таким образом, обратная величина общего (эквивалентного) со­противления R параллельно включенных потребителей равна сумме обратных величин сопротивлений этих потребителей.

Величина, обратная сопротивлению, определяет проводимость при параллельном соединении потребителей определяется сум­мой проводимостей потребителей

Если параллельно включены п одинаковых потребителей с со­противлениемR` каждый, то эквивалентное сопротивление этих потребителейR =. Если параллельно включены два потребите ля с сопротивлениямиR₁ иR₂, то их общее (эквивалентное) со­противление в соответствии с (3.12) равно

Откуда

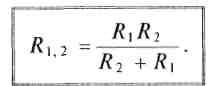
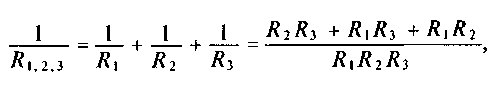
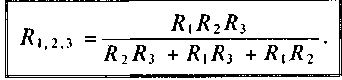
Если параллельно включены три потребителя с сопротивления­ми R₁ R₂ иRз, то общее их сопротивление (см. (3.12))

Изменение сопротивления какого-либо из параллельно соеди­ненных потребителей не влияет на режим работы (напряжение) других потребителей, включая изменяемое. Поэтому параллель­ное соединение нашло широкое практическое применение. При параллельном соединении потребителей на большем со­противлении тратится меньшая мощность:

Рассчитаем общее сопротивление цепи рисунок1

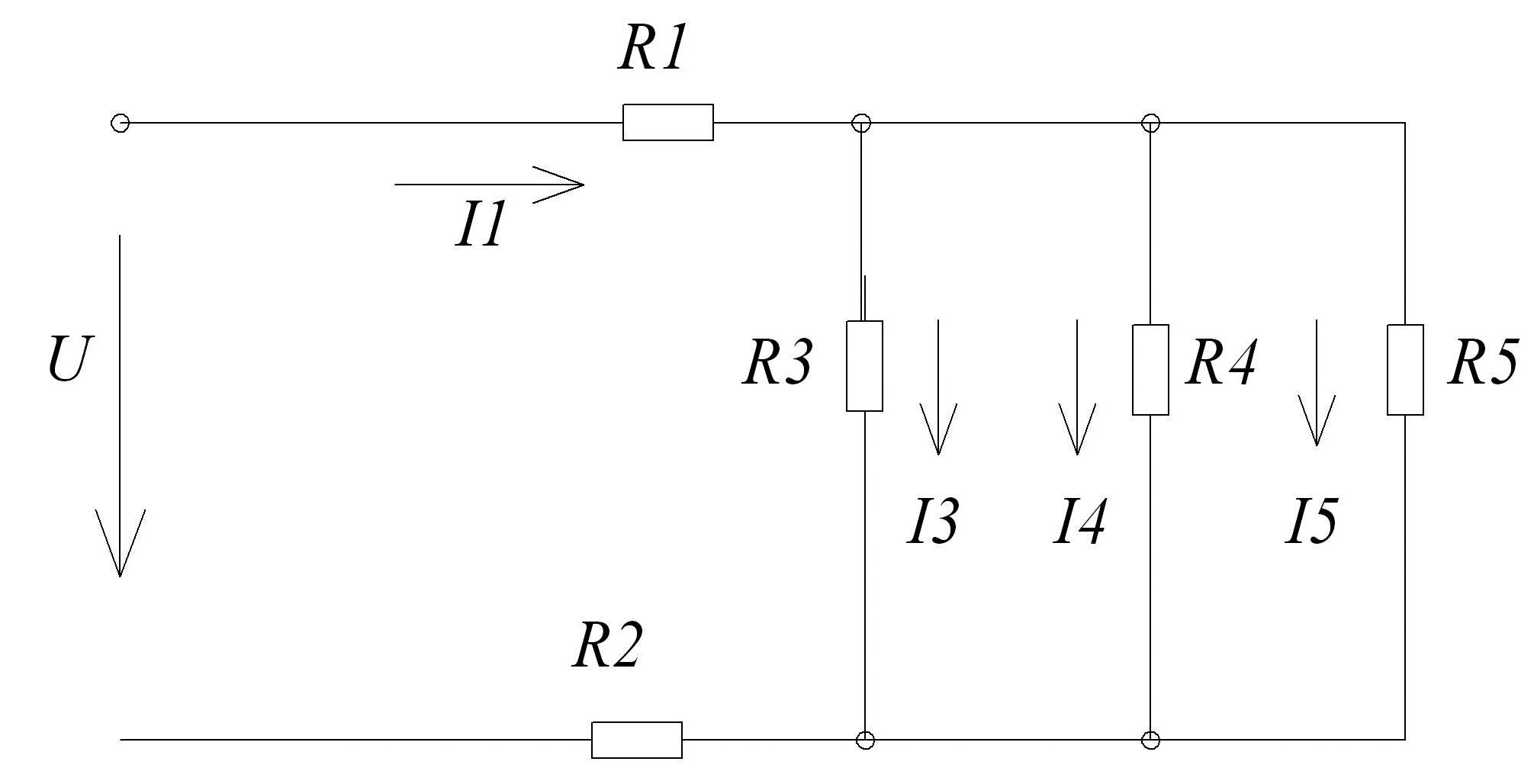
Рисунок 1- Схема электрическая

R₃₄₅=R₃R₄R₅/(R₃ R₄+R₅R₃+R₅ R₄)

R_общ=R₁+R₃₄₅+R₂

12. Запишите алгоритм расчета электрической цепи постоянного тока методом узловых и контурных уравнений для схемы рисунок 3 .

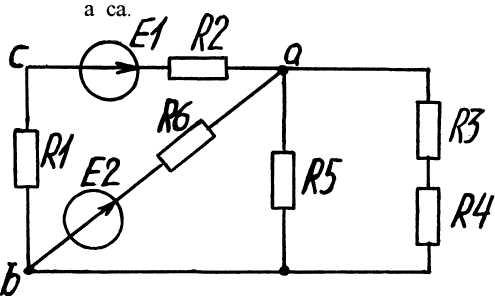
Рисунок 3- Схема электрическая

Алгоритм:

1. Выбираем направление действительных токов

2. Составляем систему уравнений (количество уравнений в системе равно количеству токов в цепи)

3. По первому закону Кирхгофа составляем m-1 уравнений, где m – это число узлов

4. Оставшиеся уравнения составляем по второму закону Кирхгофа. n-m+1 кол-во оставшихся уравнений, где n – число ветвей, m – число узлов

5. Решая данную систему, находим действительные токи

6. Составляем баланс мощностей

В цепи четыре тока, следовательно, в системе четыре уравнений.

По 1 закону Кирхгофа составляем 1 уравнение

I1 + I2– I3 – I4 = 0

По 2 закону Кирхгофа составляем ещё 3 уравнения

E1–E2 = I1∙(R1 + r1+ R2) – I2∙(R6+ r2 )

E2 = I2∙( r2+ R6) – I3∙R5

0 =– I3∙R5 + I4∙R4 + I4∙R3

Получим систему уравнений:

I1 + I2– I3 – I4 = 0

E1–E2 = I1∙(R1 + r1+ R2) – I2∙(R6+ r2 )

E2 = I2∙( r2+ R6) – I3∙R5

0 =– I3∙R5 + I4∙R4 + I4∙R3

Составляем баланс мощностей

E₁∙ I1+E₂∙ I2=I₁²∙( R1 + r1+ R2)+ I₂²∙(R6 + r2)+I₃²∙R5 +I₄²∙R4 +I₄²∙R3

13.Запишите алгоритм расчета электрической цепи постоянного тока методом контурных токов для схемы рисунок 4

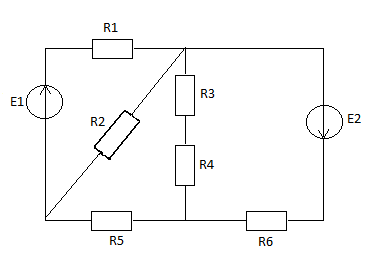
Рисунок 4- Схема электрическая

Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1.

Достигается это разделением схемы на независимые контуры и введением для каждого контура своего тока, являющегося расчетной величиной.

Алгоритм решения задач:

1. Выбираем направление действительных токов.

2. Определяем независимые контуры и выбираем в них направление контурных токов.

3. Составляем систему уравнений (количество уравнений равно количеству независимых контуров).

4. Уравнения составляем по правилу: левая часть представляет собой алгебраическую сумму ЭДС, входящих в контур. Правая часть уравнения представляет собой сумму из нескольких слагаемых. Первое слагаемое (оно всегда положительное)- это произведение контурного тока и собственного сопротивления контура (сумма всех сопротивлений в данном контуре). Следующее слагаемое – это произведение смежного контурного тока на общее сопротивление двух контуров. Оно положительно, если контурные токи протекают через резистор в одном направлении или отрицательно, если в разном.

5. Решив систему, найдём контурные токи.

6. Действительные токи находим как алгебраическую сумму частных.

7. Проверку производим с помощью уравнения баланса мощностей.

Произвольно задаём направление действительных токов.

Для независимых контуров задаём направление контурных токов.

Составляем уравнения:

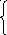E₁=II(R₁+R₂)-IШR₂

0=IIII(R₄+R₃+R₂+R₅)-IIR₂-III(R₄+R₃ )

E₂=III(R₆+R₃+R₄)- IШ (R₄+R₃ )

Решив систему, найдём контурные токи.

Действительные токи находим как алгебраическую сумму контурных токов:

I₁= II I₄= IIII

I₂= II- IIII I₅= III

I₃= IIII - III

Составляем баланс мощностей

Е₁∙I₁+E₂∙I₅= I₁²∙R₁+I₂²∙R₂+I₃^2∙(R₄+R₃ )+I₄^2∙R₅+I₅^2∙R₆