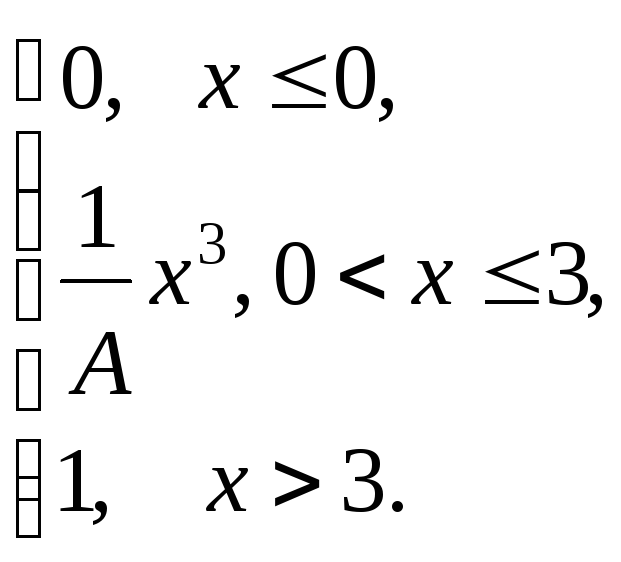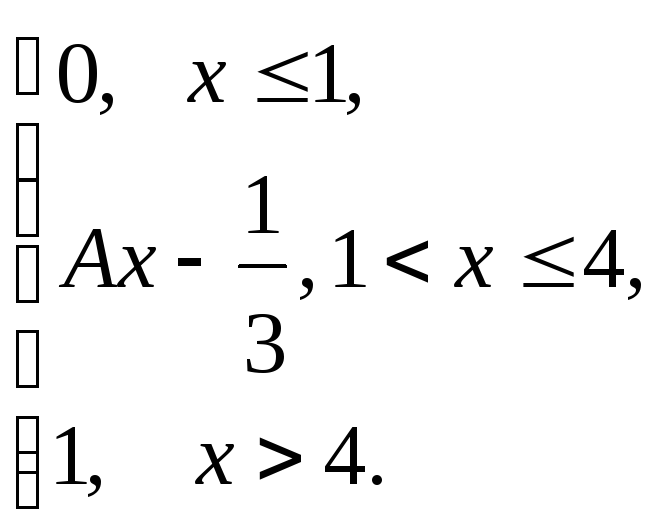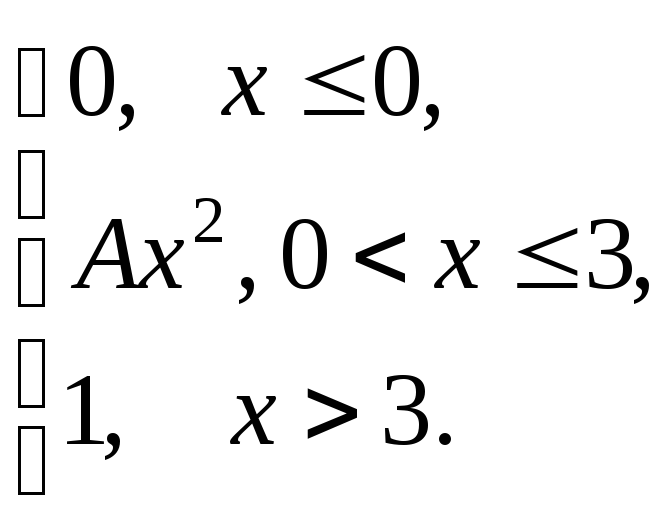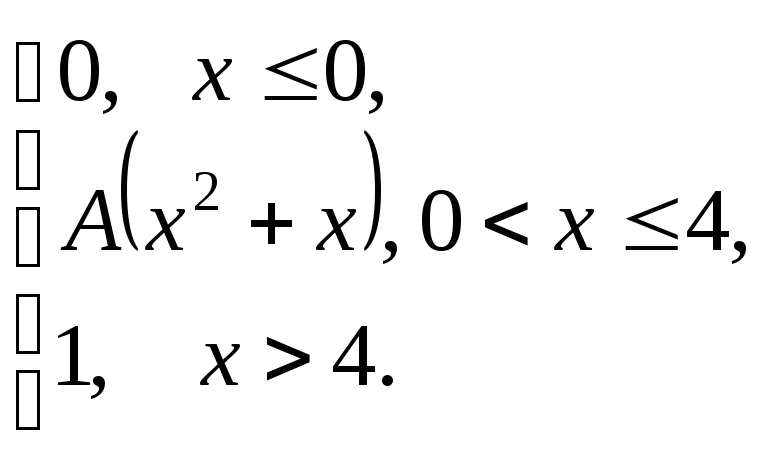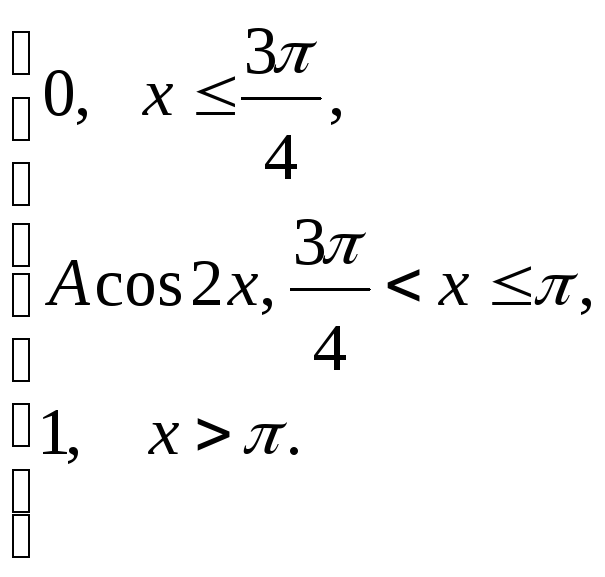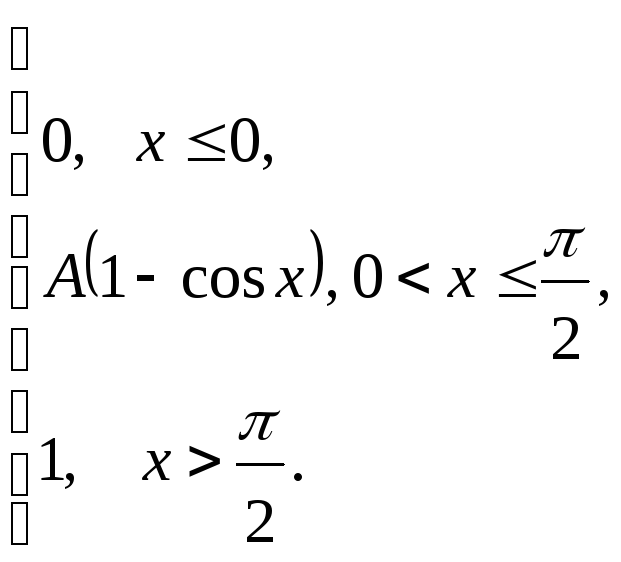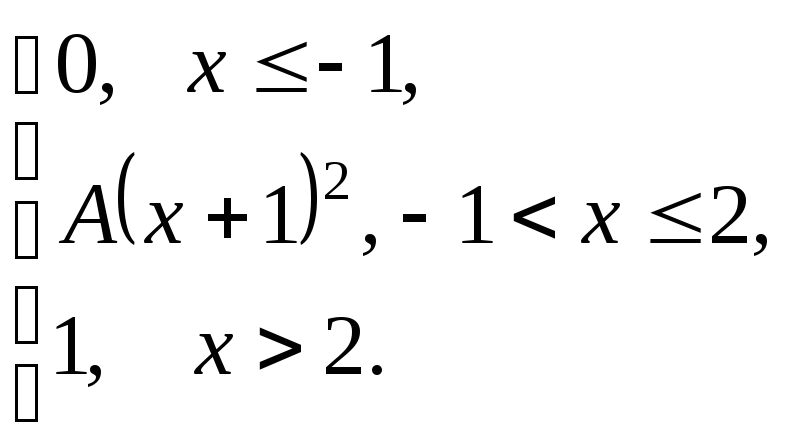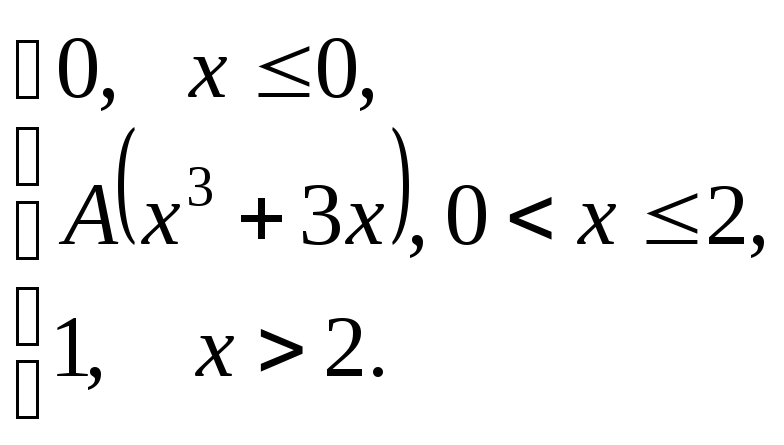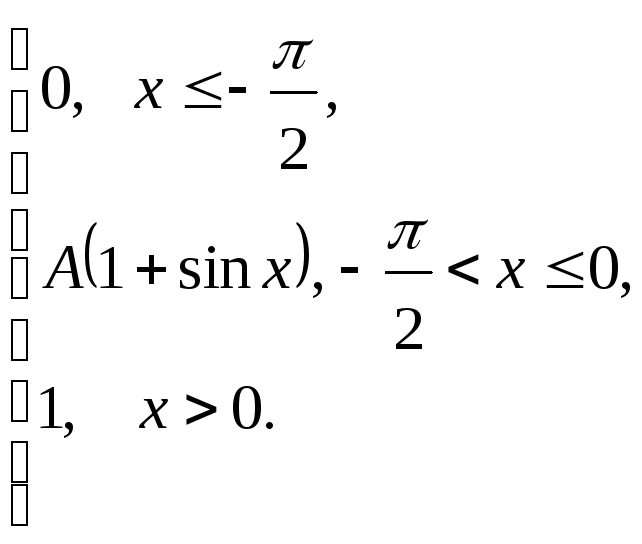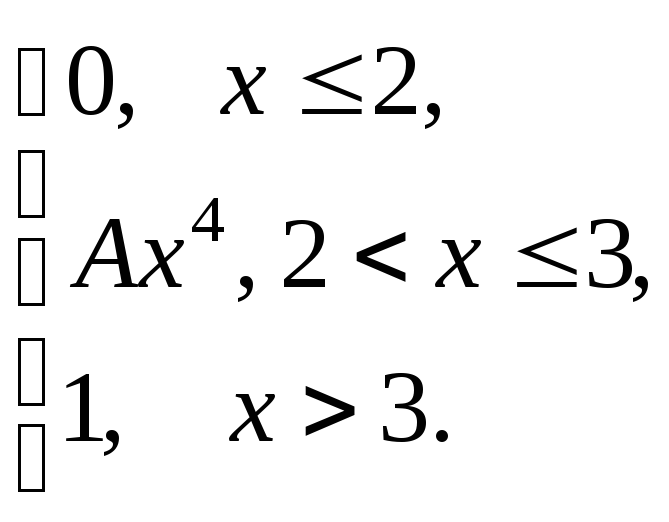- •Содержание
- •Введение
- •Раздел 1. Элементы линейной и векторной алгебры
- •Раздел 2. Аналитическая геометрия
- •Раздел 3. Введение в математический анализ
- •Раздел 4. Дифференциальное исчисление функции одной переменной.
- •Раздел 5. Функции нескольких переменных
- •Раздел 6. Неопределенный интеграл
- •Раздел 7. Определенный интеграл
- •Раздел 8. Дифференциальные уравнения
- •Раздел 9. Ряды
- •Раздел 10. Элементы теории вероятностей
- •Раздел 11. Элементы математической статистики
- •Перечень рекомендуемой литературы Учебники
- •Задачники
- •Контрольная работа №1
- •Контрольная работа № 2
- •Контрольная работа № 3
Контрольная работа № 3
Задания 131-140. Исследовать числовой ряд на сходимость.
|
131. |
132. |
|
133. |
134. |
|
135. |
136. |
|
137. |
138. |
|
139.
|
140. |
Задания 141-150. Найти область сходимости степенного ряда.
|
141.
|
142.
|
|
143.
|
144.
|
|
145.
|
146.
|
|
147.
|
148.
|
|
149.
|
150.
|
151. В течение года три фирмы могут обанкротиться независимо друг от друга с вероятностями 0,2; 0,3; 0,5. Найти вероятность того, что в конце года 1)обанкротятся ровно две фирмы; 2) хотя бы одна фирма.
152. Вероятность аудиторской проверки в течение года для Беларусбанка равна 0,8, а для Приорбанка – 0,9. Найти вероятность того, что в течение года будут проверены 1) оба банка; 2) хотя бы один банк.
153. Вероятность того, что потребитель увидит рекламу по каждому из трех телеканалов соответственно равна 0,4; 0,6; 0,7. Какова вероятность того, что потребитель увидит рекламу 1) только по одному из каналов; 2) по всем трем каналам.
154. Вероятность получения заказа в текущем году для первой строительной фирмы равна 0,95, для второй – 0,8, для третьей – 0,5. Найти вероятность того, что в текущем году 1) ни одна фирма не получит заказа; 2) две фирмы получат заказ.
155. Надежность первой компании в течение времени t оценивается на уровне 95%, второй – 70%, третьей – 80%. Найти вероятность того, что в течение времени t 1) все три компании не станут банкротами; 2) хотя бы две компании станут банкротами.
156. Вероятность того, что в течение недели покупатель посетит гипермаркет А, равна 0,85, а гипермаркет В – 0,9. Какова вероятность того, что в течение недели: 1) покупатель посетит оба магазина; 2) только один из них.
157. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый, второй и третий вопрос, соответственно, равна 0,92; 0,8 и 0,75. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить 1) на все вопросы; 2) по крайней мере на два вопроса.
158. Вероятности того, что сальдо внешней торговли будет положительным для трех стран соответственно равны 0,74; 0,83 и 0,9. Найти вероятности событий: 1) только две страны будут иметь положительное сальдо; 2) все страны будут иметь отрицательное сальдо.
159. Строительная отрасль выпускает акции трех видов А, В и С. Вероятности того, что акции через месяц поднимутся в цене соответственно равны 0,85; 0,9; 0,93. Какова вероятность того, что через месяц поднимутся в цене 1) акции только одного вида; 2) акции всех видов.
160. Предприятие состоит из трех независимо работающих подразделений. Предполагается, что вероятность их рентабельной работы за два месяца соответственно равна 0,65; 0,7; 0,82. Найти вероятность того, что в течение двух месяцев рентабельным будет 1) хотя бы одно из подразделений; 2) ровно два подразделения.
161. В бухгалтерии банка имеются два списка должников. В первом – фамилии 10 мужчин и 12 женщин, во втором – 8 мужчин и 4 женщин. Одна фамилия случайно переносится из первого списка во второй. Затем фамилия одного из должников случайно выбирается из второго списка. Найти вероятность того, что это будет фамилия мужчины.
162. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит аналогичный, равна 0,91, а при наличии конкурирующего – 0,32. Вероятность выпуска конкурентом товара равна 0,45. Найти вероятность того, что товар будет пользоваться спросом на рынке.
163. Лизинговая компания предоставляет в аренду на определенных условиях дорогостоящее оборудование с вероятностью 0,9, если экономическая ситуация в стране не будет ухудшаться в течение времени t. Если же экономическая ситуация будет ухудшаться, то эта вероятность равна 0,65. Экономист-консультант полагает, что в течение времени t с вероятностью 0,72 ситуация в стране будет становиться хуже. Чему равна вероятность того, что лизинговая компания предоставит оборудование в аренду?
164. Отдел маркетинга полагает, что в ближайшее время ожидается рост спроса на услуги данной строительной фирмы с вероятностью 0,7. Фирма, занимающаяся прогнозом рыночной ситуации, подтверждает предположение о росте спроса. Положительный прогноз фирмы сбывается на 90%, а отрицательный – на 80%. Найти вероятность того, что рост спроса действительно произойдет.
165. Три фирмы поставляют товар в данный регион в соотношении 2:3:5. Среди продукции первой фирмы высококачественные изделия составляют 85%, у второй – 90%, у третьей – 80%. Взятый наугад товар оказался отличного качества. Найти вероятность того, что он изготовлен третьей фирмой.
166. Курс евро повышается в течение полугода с вероятностью 0,7, остается неизменным с вероятностью 0,2 и понижается с вероятностью 0,1. При повышении курса предприятие надеется получить прибыль с вероятностью 0,2, при неизменном курсе – с вероятностью 0,5, при понижении курса – с вероятностью 0,8. Найти вероятность того, что предприятие получит прибыль.
167. На заводе строительного оборудования первый цех выпускает 25% всех изделий, второй – 45%, третий – 30% . В их продукции брак составляет соответственно 3%, 2%, 4%. Какова вероятность того, что случайно выбранное изделие является дефектным?
168. У студента S
есть три любимых места для прогулок,
которые он посещает с одинаковой
вероятностью. Вероятность того, что он
встретит своего друга в первом месте,
равна
![]() ,
во втором
,
во втором![]() ,
в третьем
,
в третьем![]() .
Известно, что встреча произошла. Какова
вероятность того, что студентS
выбрал первое место?
.
Известно, что встреча произошла. Какова
вероятность того, что студентS
выбрал первое место?
169. Вероятность
того, что коэффициент Джини G,
который показывает равномерность
распределения доходов среди населения
страны, будет находиться в области
![]() равна 0,07, в области
равна 0,07, в области![]() 0,8,
в области
0,8,
в области![]() 0,13.
Вероятности социальной нестабильности
общества для коэффициентаG
из областей
0,13.
Вероятности социальной нестабильности
общества для коэффициентаG
из областей
![]()
![]()
![]() соответственно равны 0,015; 0,08; 0,6. Найти
вероятность того, что данная страна
социально стабильна.
соответственно равны 0,015; 0,08; 0,6. Найти
вероятность того, что данная страна
социально стабильна.
170. Имеются две неотличимые по внешнему виду игральные кости: обычная и фальшивая, при случайном подбросе которой «шестерка» выпадает с вероятностью 1/3, «единица» - с вероятностью 1/9, а остальные цифры выпадают с одинаковой вероятностью. Подброшена наудачу выбранная кость и в результате выпала «четверка». Найти вероятность того, что была подброшена обычная игральная кость.
Задания 171-180.
Непрерывная
случайная величина (СВ) Х
задана функцией распределения![]() .
Найти:
.
Найти:
коэффициент А;
плотность распределения вероятностей
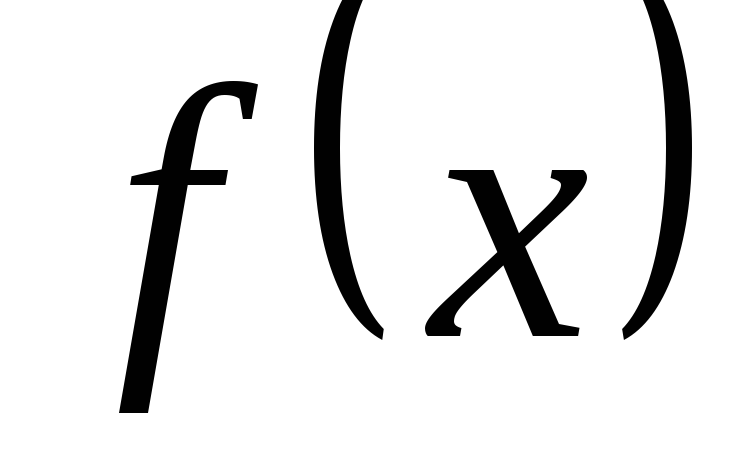 ;
;математическое ожидание СВ Х;
вероятность события
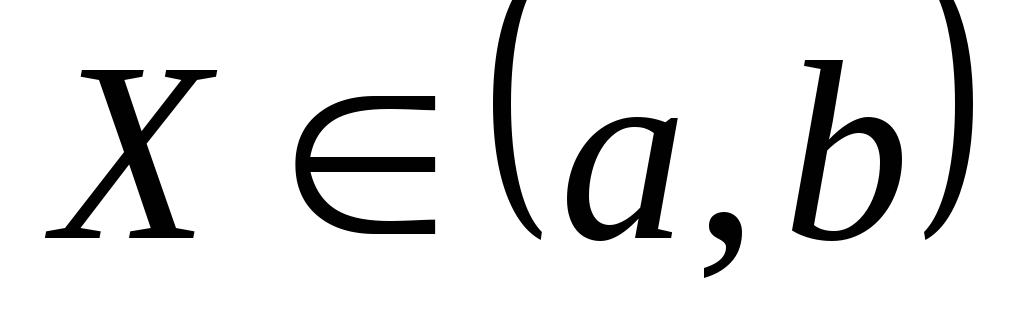 .
.
|
171. |
|
|
|
172. |
|
|
|
173. |
|
|
|
174. |
|
|
|
175. |
|
|
|
176. |
|
|
|
177. |
|
|
|
178. |
|
|
|
179. |
|
|
|
180. |
|
|
Задания 181-190.
Зависимость выпуска валовой продукции (СВ Y) от стоимости основных фондов (СВ Х) 50 предприятий представлена корреляционной таблицей.
Требуется:
Найти уравнение прямой линии регрессии Y на Х.
Найти уравнение прямой линии регрессии Х на Y.
Построить графики полученных прямых.
Оценить тесноту корреляционной связи, используя выборочный коэффициент корреляции.
|
181. |
Х Y |
0,8 |
2,4 |
4,0 |
5,6 |
7,2 |
mi |
|
0,7 |
2 |
1 |
|
|
|
3 | |
|
2,1 |
|
6 |
5 |
|
|
11 | |
|
3,5 |
|
|
3 |
20 |
3 |
26 | |
|
4,9 |
|
|
4 |
3 |
1 |
8 | |
|
6,3 |
|
|
|
|
2 |
2 | |
|
mj |
2 |
7 |
12 |
23 |
6 |
50 |
|
182. |
Х Y |
0,7 |
2,1 |
3,5 |
4,9 |
6,3 |
mi |
|
0,4 |
1 |
2 |
|
|
|
3 | |
|
1,2 |
2 |
4 |
3 |
|
|
9 | |
|
2,0 |
|
|
19 |
4 |
3 |
26 | |
|
2,8 |
|
|
1 |
8 |
2 |
11 | |
|
3,6 |
|
|
|
|
1 |
1 | |
|
mj |
3 |
6 |
23 |
12 |
6 |
50 |
|
183. |
Х Y |
0,8 |
2,0 |
3,2 |
4,4 |
5,6 |
mi |
|
0.6 |
3 |
4 |
1 |
|
|
8 | |
|
1,4 |
1 |
5 |
10 |
8 |
|
24 | |
|
2,2 |
1 |
3 |
1 |
5 |
1 |
11 | |
|
3,0 |
|
|
|
2 |
3 |
5 | |
|
3,8 |
|
|
1 |
|
1 |
2 | |
|
mj |
5 |
12 |
13 |
15 |
5 |
50 |
|
184. |
Х Y |
1,2 |
2,4 |
3,6 |
4,8 |
6,0 |
mi |
|
1,8 |
2 |
2 |
|
|
|
4 | |
|
3,6 |
|
4 |
5 |
|
|
9 | |
|
5,4 |
|
1 |
3 |
20 |
2 |
26 | |
|
7,2 |
|
|
4 |
3 |
1 |
8 | |
|
8,0 |
|
|
|
|
3 |
3 | |
|
mj |
2 |
7 |
12 |
23 |
6 |
50 |
|
185. |
Х Y |
0,6 |
1,2 |
1,8 |
2,4 |
4,0 |
mi |
|
1,4 |
1 |
1 |
|
|
|
2 | |
|
2,8 |
2 |
10 |
2 |
|
|
14 | |
|
4,2 |
1 |
3 |
19 |
|
|
23 | |
|
5,6 |
|
|
4 |
4 |
|
8 | |
|
7,0 |
|
|
|
1 |
2 |
3 | |
|
mj |
4 |
14 |
25 |
5 |
2 |
50 |
|
186. |
Х Y |
0,7 |
1,4 |
2,1 |
2,8 |
3,5 |
mi |
|
1,6 |
4 |
3 |
1 |
|
|
8 | |
|
3,2 |
1 |
5 |
12 |
7 |
|
25 | |
|
4,8 |
1 |
3 |
1 |
6 |
|
11 | |
|
6,4 |
|
|
1 |
2 |
2 |
5 | |
|
8,0 |
|
|
|
|
1 |
1 | |
|
mj |
6 |
11 |
15 |
15 |
3 |
50 |
|
187. |
Х Y |
0,9 |
1,8 |
2,7 |
3,6 |
4,5 |
mi |
|
1,1 |
1 |
2 |
|
|
|
3 | |
|
2,2 |
1 |
5 |
|
|
|
6 | |
|
3,3 |
|
1 |
20 |
8 |
|
29 | |
|
4,4 |
|
|
6 |
1 |
3 |
10 | |
|
5,5 |
|
|
|
|
2 |
2 | |
|
mj |
2 |
8 |
26 |
9 |
5 |
50 |
|
188. |
Х Y |
1,6 |
3,2 |
4,8 |
6,4 |
8,0 |
mi |
|
1,2 |
2 |
5 |
|
|
|
7 | |
|
2,4 |
|
1 |
9 |
2 |
|
12 | |
|
3,6 |
|
1 |
16 |
3 |
2 |
22 | |
|
4,8 |
|
|
1 |
1 |
5 |
7 | |
|
6,0 |
|
|
|
|
2 |
2 | |
|
mj |
2 |
7 |
26 |
6 |
9 |
50 |
|
189. |
Х Y |
1,3 |
2,6 |
3,9 |
5,2 |
6,5 |
mi |
|
1,9 |
1 |
2 |
|
|
|
3 | |
|
3,8 |
3 |
6 |
3 |
|
|
12 | |
|
5,7 |
|
2 |
18 |
4 |
|
24 | |
|
7,6 |
|
|
1 |
7 |
1 |
9 | |
|
9,5 |
|
|
|
|
2 |
2 | |
|
mj |
4 |
10 |
22 |
11 |
3 |
50 |
|
190. |
Х Y |
0,4 |
0,8 |
1,2 |
1,6 |
2,0 |
mi |
|
0,5 |
3 |
2 |
1 |
|
|
6 | |
|
1,0 |
1 |
2 |
7 |
1 |
|
11 | |
|
1,5 |
1 |
3 |
2 |
18 |
2 |
26 | |
|
2,0 |
|
|
|
|
5 |
5 | |
|
2,5 |
|
|
|
|
2 |
2 | |
|
mj |
5 |
7 |
10 |
19 |
9 |
50 |
Методические указания для выполнения контрольной работы № 1.
Решение задания типа 1-10.
При условном
делении экономики на три отрасли задана
матрица коэффициентов прямых затрат
 и вектор конечной продукции
и вектор конечной продукции![]() .
Требуется:
.
Требуется:
Записать уравнение линейного межотраслевого баланса в координатной форме.
Найти плановые объемы выпуска валовой продукции отраслей. Систему линейных алгебраических уравнений решить методом Гаусса. Решение системы записать в неправильных дробях.
Выполнить проверку результата.
Записать приближенный ответ с точностью до сотых.
1. Уравнение
линейного межотраслевого баланса имеет
вид
![]() ,
где
,
где![]() вектор
валового выпуска продукции,
вектор
валового выпуска продукции,![]() вектор
конечного потребления,
вектор
конечного потребления,![]() матрица
прямых материальных затрат. Известны
вектор конечного потребления
матрица
прямых материальных затрат. Известны
вектор конечного потребления![]() и матрица прямых материальных затрат
и матрица прямых материальных затрат .
.
Подставим в
уравнение Леонтьева
![]() векторы
векторы![]() и матрицуА:
и матрицуА:
![]()

![]() .
.
Используя правила умножения матриц, сложения векторов и определение равенства векторов, получаем систему уравнений:
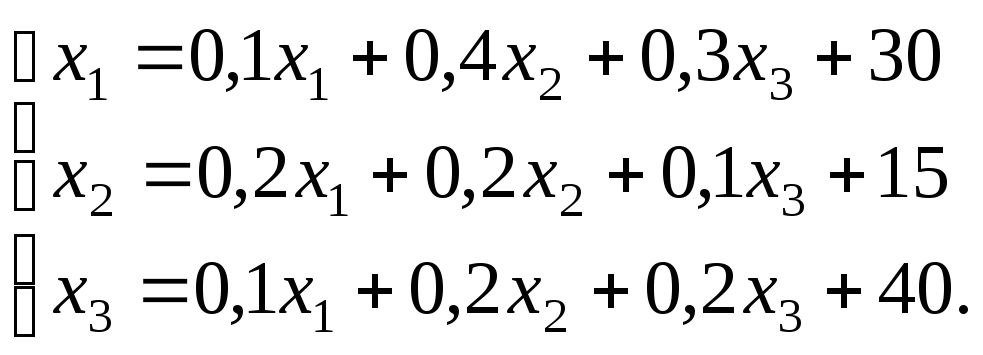
Полученная система – это векторное уравнение линейного межотраслевого баланса в координатной форме.
Для решения этой системы приведем подобные члены:
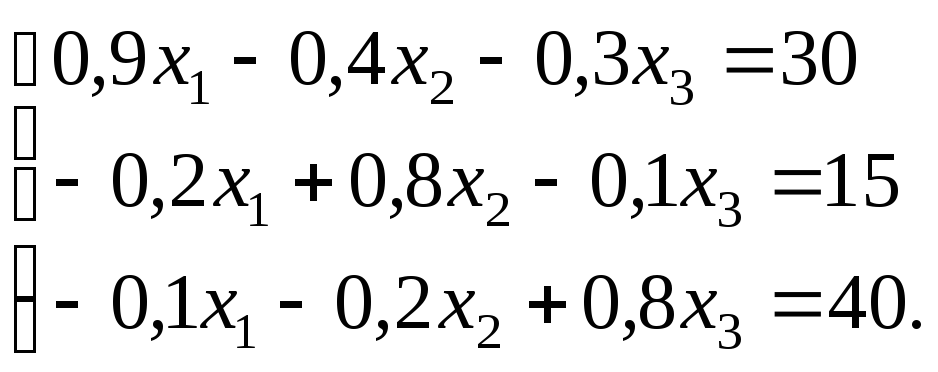
Все уравнения умножим на 10:
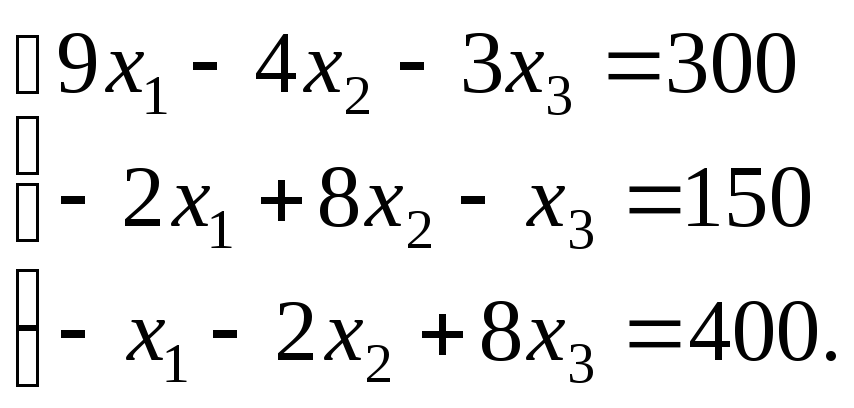
2. Решим полученную систему методом Гаусса. Основная его идея состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему специального вида, где одно из уравнений содержит все неизвестные, второе – на одно неизвестное меньше, и т.д., последнее уравнение содержит лишь одно из неизвестных. Эти преобразования называют прямым ходом метода Гаусса.
Для удобства вычислений третье уравнение поставим первым, и оно будет ведущим на первом этапе вычислений:
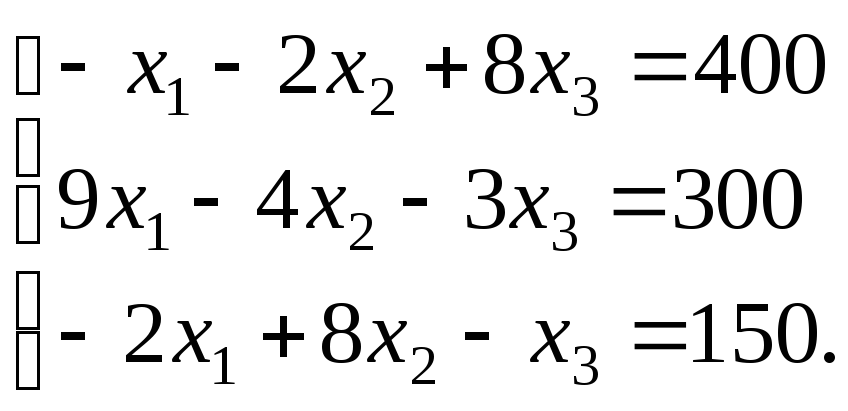
Исключим неизвестную
![]() из второго уравнения. Для этого умножим
первое уравнение на 9 и прибавим ко
второму:
из второго уравнения. Для этого умножим
первое уравнение на 9 и прибавим ко
второму:
![]() .
.
Исключим неизвестную
![]() из третьего уравнения. Для этого умножим
первое уравнение на (–2) и прибавим к
третьему:
из третьего уравнения. Для этого умножим
первое уравнение на (–2) и прибавим к
третьему:
![]()
Получаем систему:
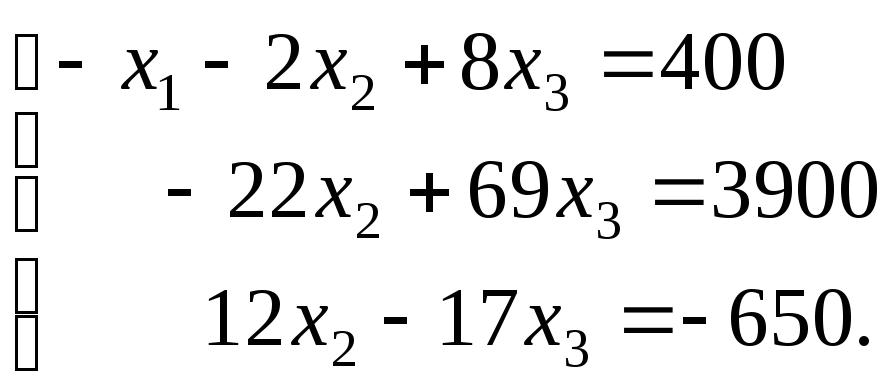
Исключим неизвестную
![]() из третьего уравнения. Для этого второе
уравнение разделим на 22, умножим на 12 и
прибавим к третьему:
из третьего уравнения. Для этого второе
уравнение разделим на 22, умножим на 12 и
прибавим к третьему:
![]() или 454х3
= 32500 или 227х3
= 16250.
или 454х3
= 32500 или 227х3
= 16250.
Получаем систему:
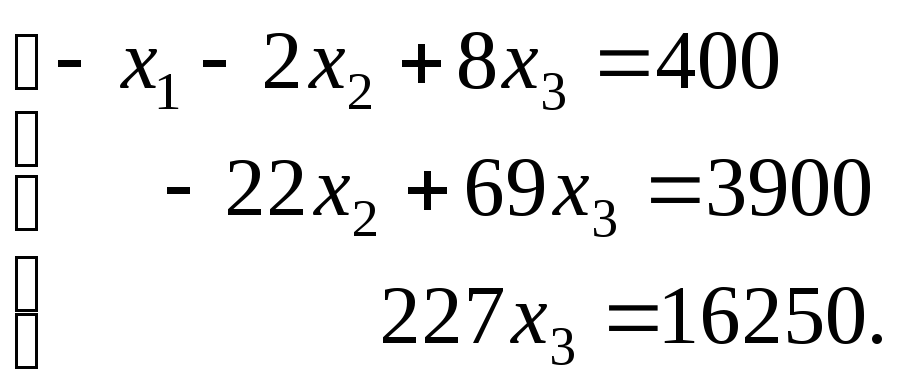
Замечание.
Преобразования в методе Гаусса удобнее выполнять не с самой системой уравнений, а с расширенной матрицей системы, которая состоит из коэффициентов при неизвестных и столбца свободных членов:
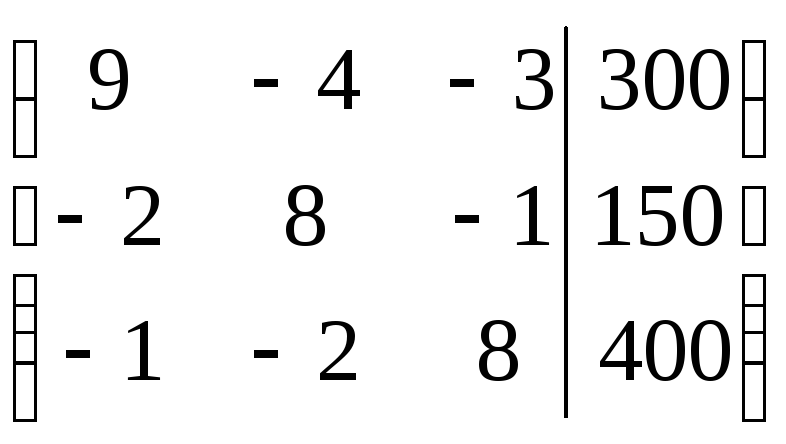
 ~
~
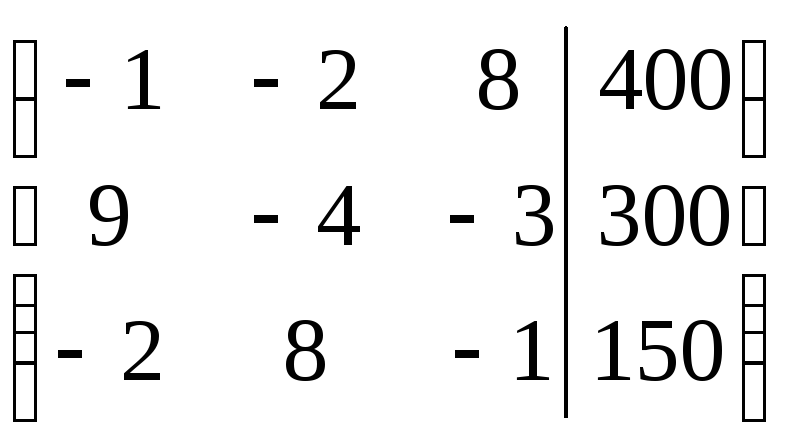
 ~
~
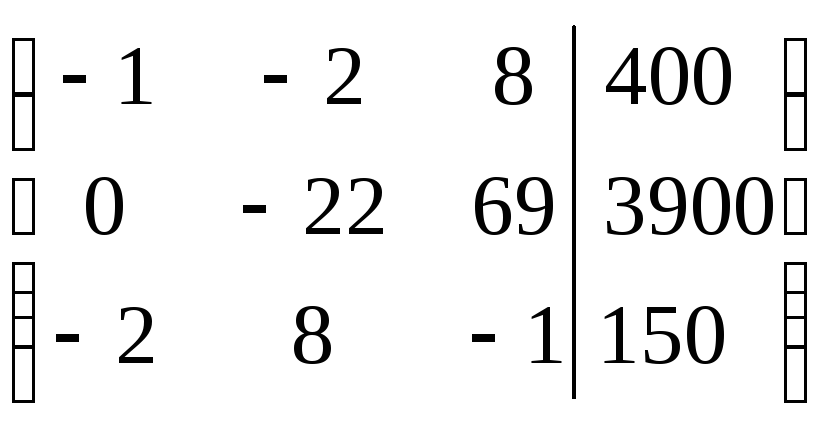
 ~
~
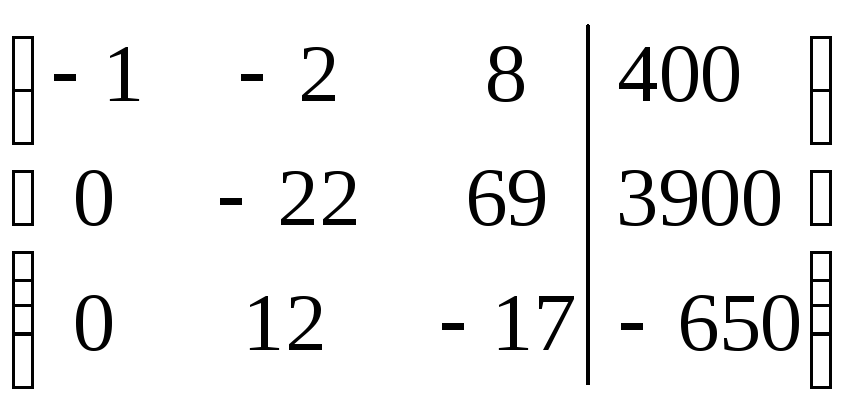
 .
.
Используя полученную матрицу, выпишем преобразованную систему:
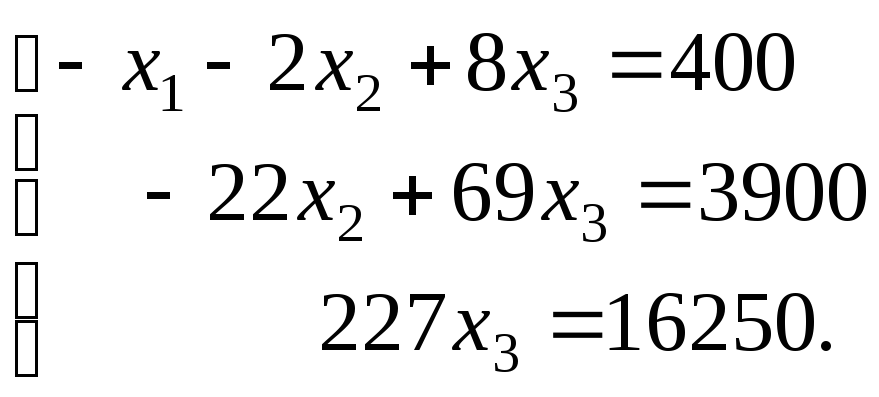
Прямой ход метода
Гаусса закончен. Обратный ход заключается
в том, что из последнего уравнения
находят неизвестную
![]() ,
затем из второго –
,
затем из второго –![]() ,
а из первого –
,
а из первого –![]() .
Выполним это:
.
Выполним это:
![]() ,
,
![]() =
=![]()
![]() ,
,
![]() =
=![]() .
.
Итак, решение
системы в неправильных дробях будет
иметь вид:
![]() ,
,![]() ,
,![]() .
Они будут выражать плановые объемы
выпуска валовой продукции отраслей.
.
Они будут выражать плановые объемы
выпуска валовой продукции отраслей.
3. Выполним проверку полученного результата. Для этого подставим эти значения в исходную систему:
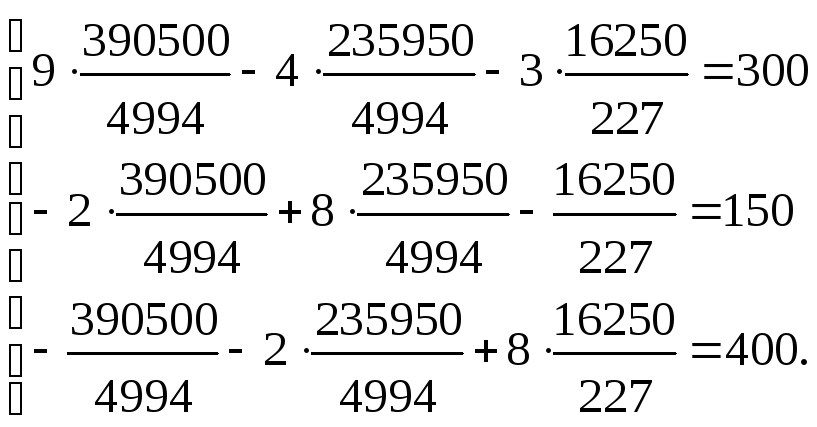
Вычисляя, получаем верные равенства.
4. Запишем приближенный
ответ с точностью до сотых:
![]() ;
;![]() ;
;![]() .
.
Решение задания
типа 11-20.
Даны векторы
![]() в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы![]() образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора![]() в этом базисе. Систему линейных уравнений
решить по формулам Крамера.
в этом базисе. Систему линейных уравнений
решить по формулам Крамера.
Например,
![]()
Решение. Для того,
чтобы векторы
![]() образовывали базис, необходимо показать,
что векторы некомпланарны, т.е. их
смешанное произведение
образовывали базис, необходимо показать,
что векторы некомпланарны, т.е. их
смешанное произведение![]() отлично от нуля.
отлично от нуля.
Вычислим смешанное
произведение
![]() с помощью определителя третьего порядка:
с помощью определителя третьего порядка:
![]() =
=
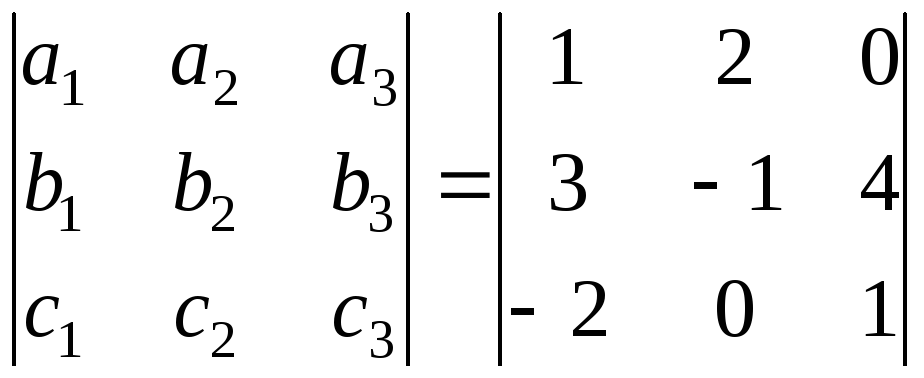 = -23.
= -23.
Поскольку
![]() = -23
= -23![]() 0,
то векторы
0,
то векторы![]() образуют базис в пространствеR3.
образуют базис в пространствеR3.
Следовательно,
любой вектор
![]() этого пространства единственным образом
можно представить в виде
этого пространства единственным образом
можно представить в виде![]() =
=![]() ,
где
,
где![]() - координаты вектора
- координаты вектора![]() в базисе
в базисе![]() .
.
От векторного равенства перейдем к равенствам над соответствующими компонентами:
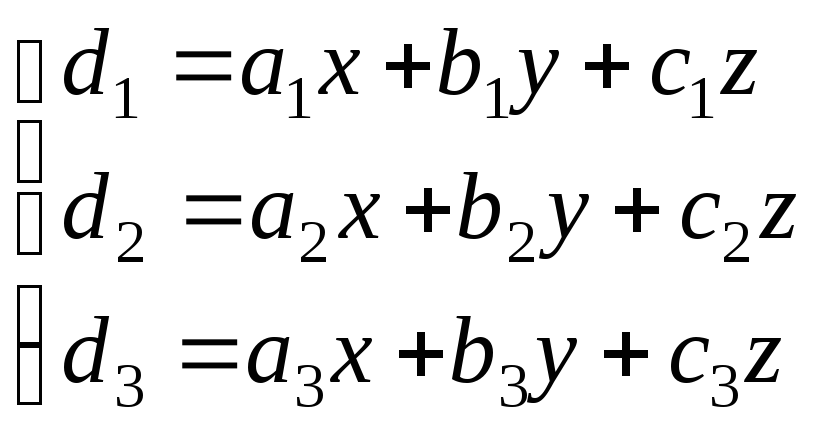 или
или
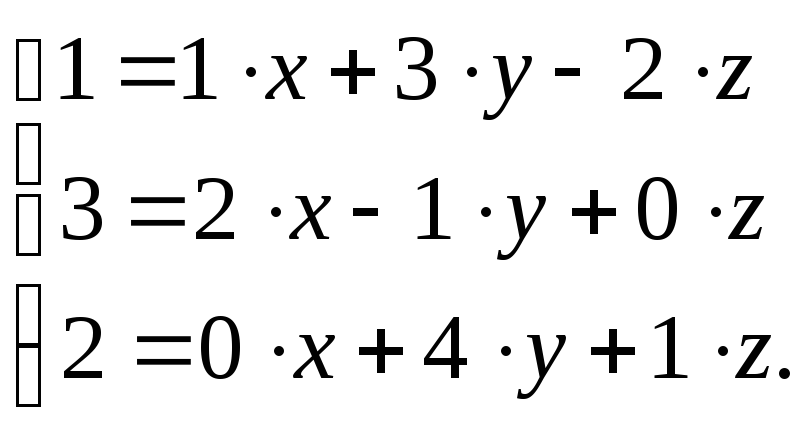
Получили систему
трех линейных уравнений с тремя
неизвестными
![]() координаты вектора
координаты вектора![]() в новом базисе.
в новом базисе.
Решаем полученную систему методом Крамера, в соответствии с которым:
1) система трех
линейных уравнений с тремя неизвестными
имеет единственное решение, если
![]() - определитель третьего порядка,
составленный из коэффициентов системы,
не равен 0.
- определитель третьего порядка,
составленный из коэффициентов системы,
не равен 0.
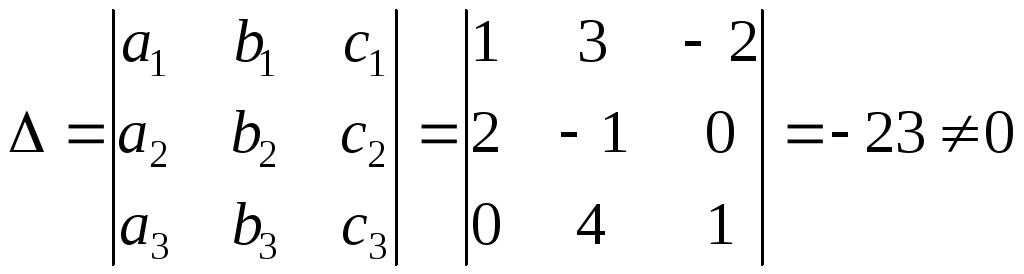
2) неизвестные
![]() находим по формулам Крамера
находим по формулам Крамера
![]() ,
,
где
![]() - определители третьего порядка,
составленные из определителя системы
- определители третьего порядка,
составленные из определителя системы![]() заменой коэффициентов, стоящих в системе
перед
заменой коэффициентов, стоящих в системе
перед![]() ,
свободными членами соответственно:
,
свободными членами соответственно:
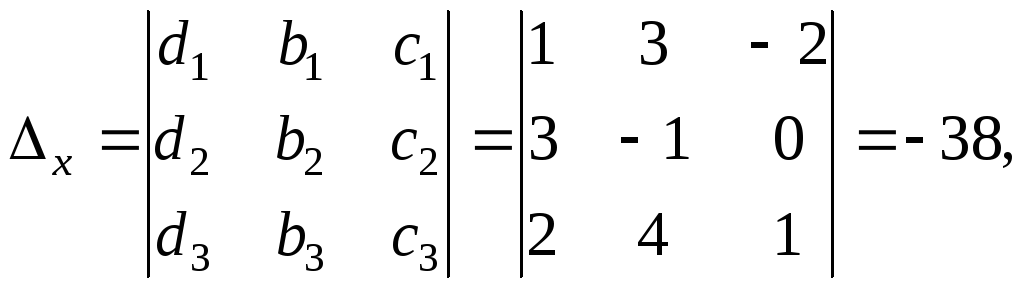
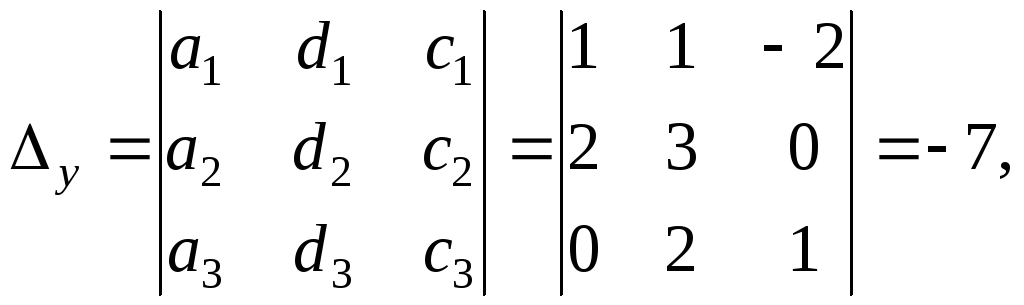
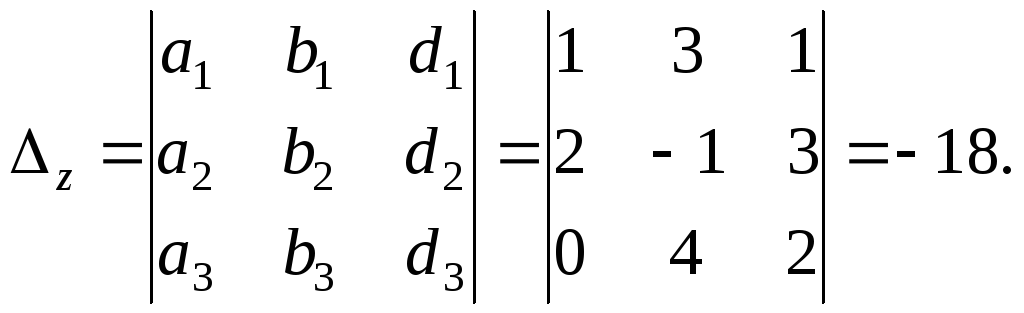
Тогда по формулам Крамера:
![]()
Проверка.
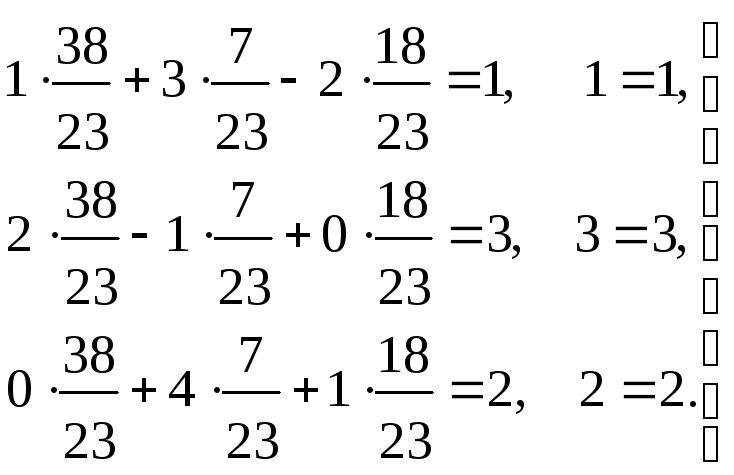
Получили тождества. Следовательно, система решена верно.
Ответ: 1) векторы
![]() образуют базис, 2) вектор
образуют базис, 2) вектор![]() в базисе
в базисе![]() имеет следующее разложение:
имеет следующее разложение:
![]() =
=![]() .
.
Решение типового задания 21-30.
Даны координаты
вершин пирамиды
![]() ,
,![]() ,
,![]() ,
,![]() .
Найти: 1). площадь грани
.
Найти: 1). площадь грани![]() ;
2). объем пирамиды; 3). уравнения прямой
;
2). объем пирамиды; 3). уравнения прямой![]() ;
4). уравнение плоскости
;
4). уравнение плоскости![]() ;
5). уравнения высоты
;
5). уравнения высоты![]() ,
опущенной из вершины
,
опущенной из вершины![]() на грань
на грань![]() ;
6). длину высоты
;
6). длину высоты![]() ;
7). координаты точки пересечения высоты
;
7). координаты точки пересечения высоты![]() с плоскостью
с плоскостью![]() .
.
Например, A1(3;5;4), A2(6;9;4), A3(0;7;2), A4(2;3;7).
1) Для нахождения
площади грани
![]() воспользуемся геометрическим смыслом
модуля векторного произведения
воспользуемся геометрическим смыслом
модуля векторного произведения![]() ,
равного площади параллелограмма,
построенного на векторах
,
равного площади параллелограмма,
построенного на векторах![]()
![]() и
и![]() как на сторонах.
как на сторонах.
Найдем векторное произведение
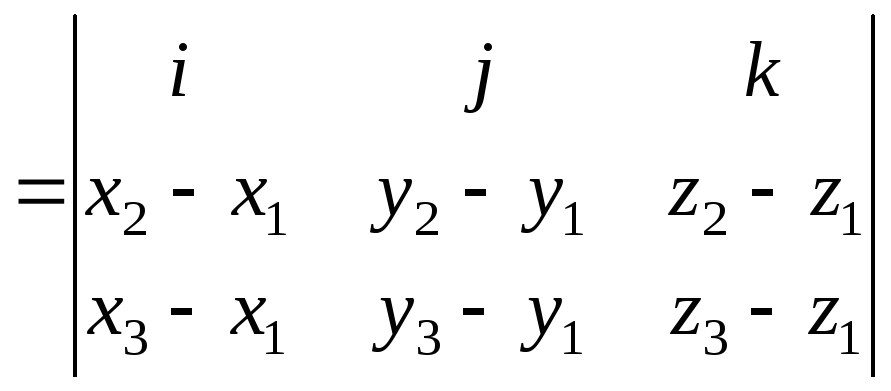
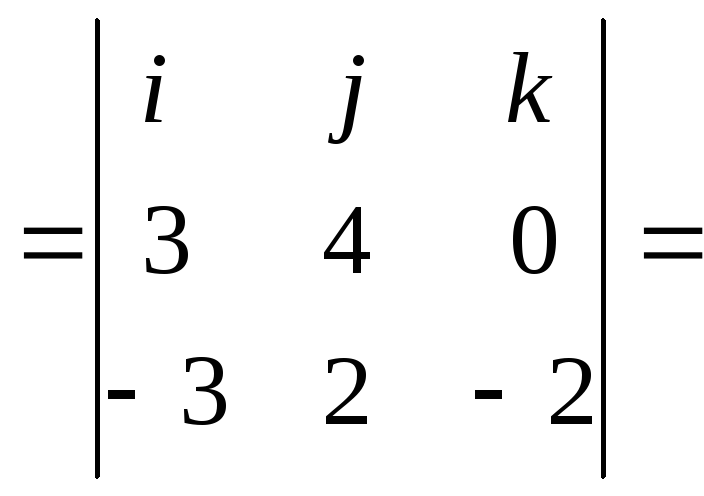
![]()
![]()
![]()
Тогда искомая
площадь грани
![]() равна:
равна:
![]() =
=![]() (ед2).
(ед2).
2) Объем пирамиды
найдем, используя геометрический смысл
модуля смешанного произведения
![]() ,
равного объему параллелепипеда,
построенного на векторах
,
равного объему параллелепипеда,
построенного на векторах![]() как на ребрах.
как на ребрах.
Вычислим смешанное
произведение векторов
![]() :
:
![]() =
=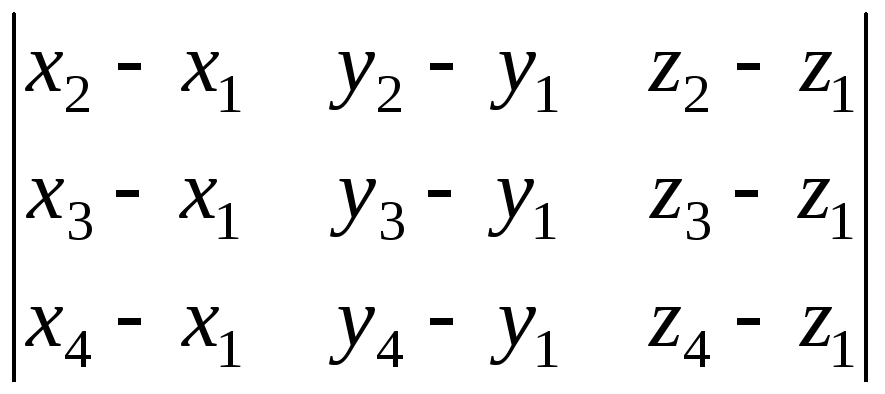 =
=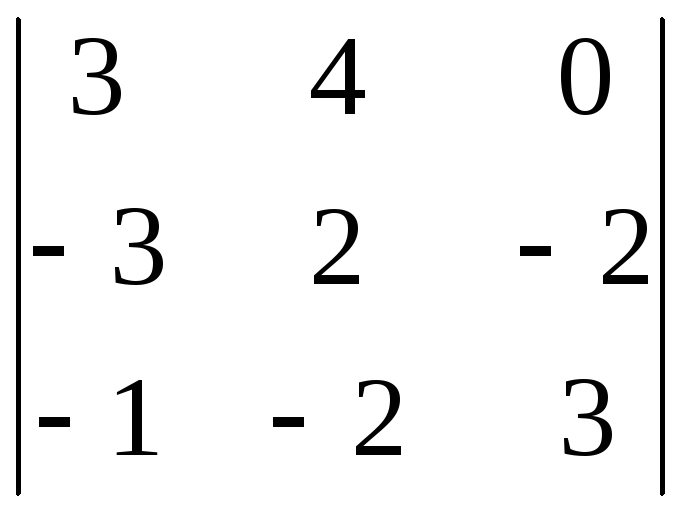 = 38.
= 38.
Так как объем пирамиды составляет шестую часть объема соответствующего параллелепипеда, то
Vпир
=
![]() =
=![]() (ед3).
(ед3).
3) Чтобы найти
уравнения прямой
![]() ,
используем уравнения прямой в пространстве,
проходящей через две известные точки
,
используем уравнения прямой в пространстве,
проходящей через две известные точки![]() и
и![]()
![]() .
.
Уравнения прямой
![]() принимают вид:
принимают вид:
![]() или
или
![]() .
.
4) Для получения
уравнения грани
![]() используем уравнение плоскости,
проходящей через три данные точки
используем уравнение плоскости,
проходящей через три данные точки![]() :
: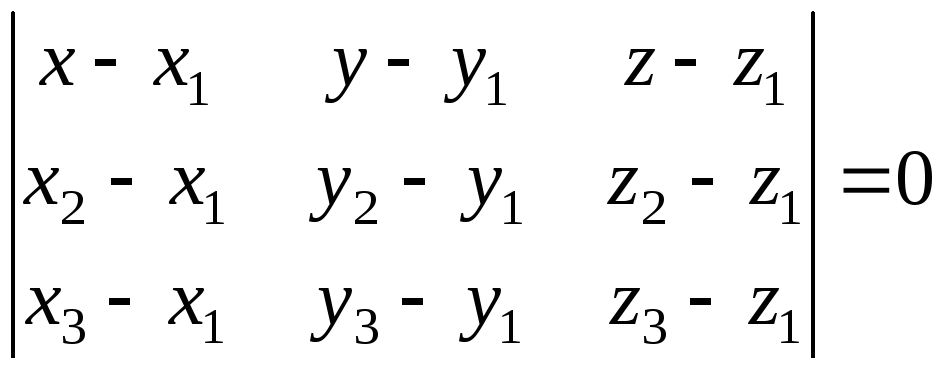 .
.
В нашей задаче: 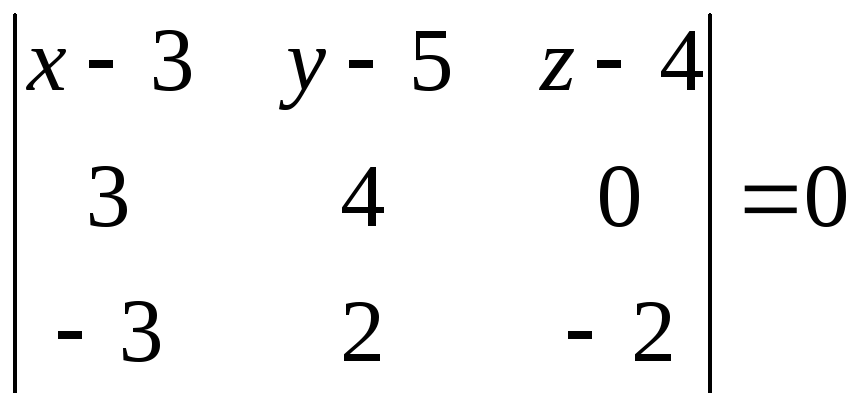 .
.
Определитель вычислим методом разложения по элементам первой строки.
![]() ,
раскрыв скобки, и приведя подобные,
получаем – 8x
+ 6y
+ 18z
– 78 = 0,
сократив на (–2), искомое уравнение будет
иметь вид 4x
– 3y
– 9z
+ 39 = 0.
,
раскрыв скобки, и приведя подобные,
получаем – 8x
+ 6y
+ 18z
– 78 = 0,
сократив на (–2), искомое уравнение будет
иметь вид 4x
– 3y
– 9z
+ 39 = 0.
5) Чтобы найти
уравнения высоты, опущенной из вершины
А4
на грань
![]() ,
используем канонические уравнения
прямой в пространстве, проходящей через
известную точкуА4
с направляющим вектором
,
используем канонические уравнения
прямой в пространстве, проходящей через
известную точкуА4
с направляющим вектором
![]()
![]() .
.
Так как высота
перпендикулярна грани
![]() ,
то в качестве направляющего вектора
,
то в качестве направляющего вектора
![]() можно использовать нормальный вектор
плоскости
можно использовать нормальный вектор
плоскости
![]() ,
координатами которого являются
коэффициенты при
,
координатами которого являются
коэффициенты при![]() в полученном уравнении грани
в полученном уравнении грани![]() :
:![]() .
.
Итак, уравнения высоты примут вид:
![]() .
.
6) Для вычисления
длины высоты
![]() примем формулу расстояния от точки
примем формулу расстояния от точки![]() до плоскости
до плоскости
![]() .
.
![]() ,
,
где
![]() – коэффициенты и свободный член из
уравнения плоскости
– коэффициенты и свободный член из
уравнения плоскости
![]() .
.
Таким образом,
![]() .
.
Координаты точки
пересечения высоты
![]() с плоскостью
с плоскостью
![]() получаются как результат решения
системы, составленной из уравнения
грани
получаются как результат решения
системы, составленной из уравнения
грани![]() и уравнений высоты
и уравнений высоты
![]() .
.
Запишем уравнения
высоты
![]() в параметрической форме:
в параметрической форме:
![]() ,
,
где t
– параметр, тогда
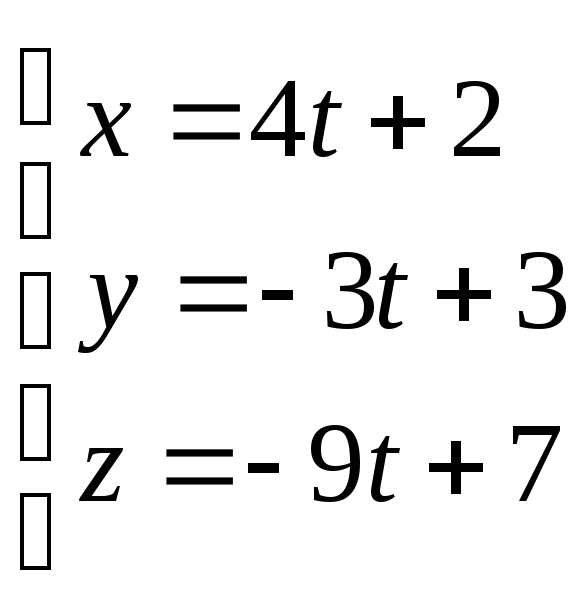 .
Решая систему
.
Решая систему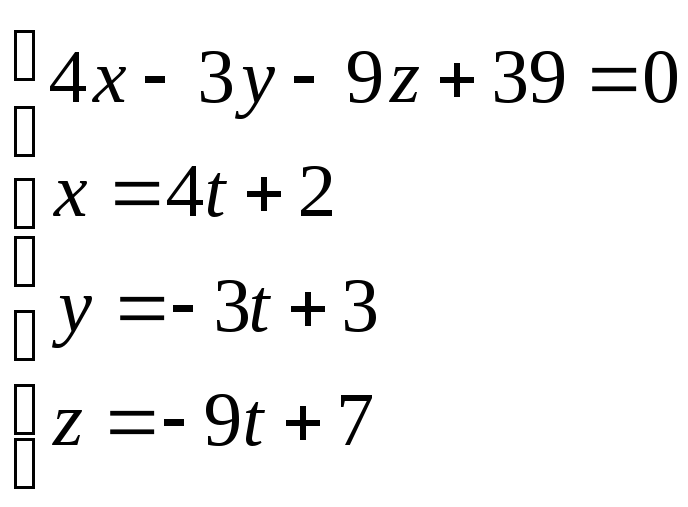 ,
,
найдем значение
параметра t.
Подставляя выражения
![]() в первое уравнение, получим
в первое уравнение, получим
![]()
![]()
![]() .
.
Искомые координаты точки пересечения:
![]() ;
;
![]() ;
;![]() .
.
Решение задания типа 31-40 со следующим условием:
Известны уравнения
двух сторон ромба
![]() и
и![]() и уравнение одной из его диагоналей
и уравнение одной из его диагоналей![]() .
Найти уравнение второй диагонали.
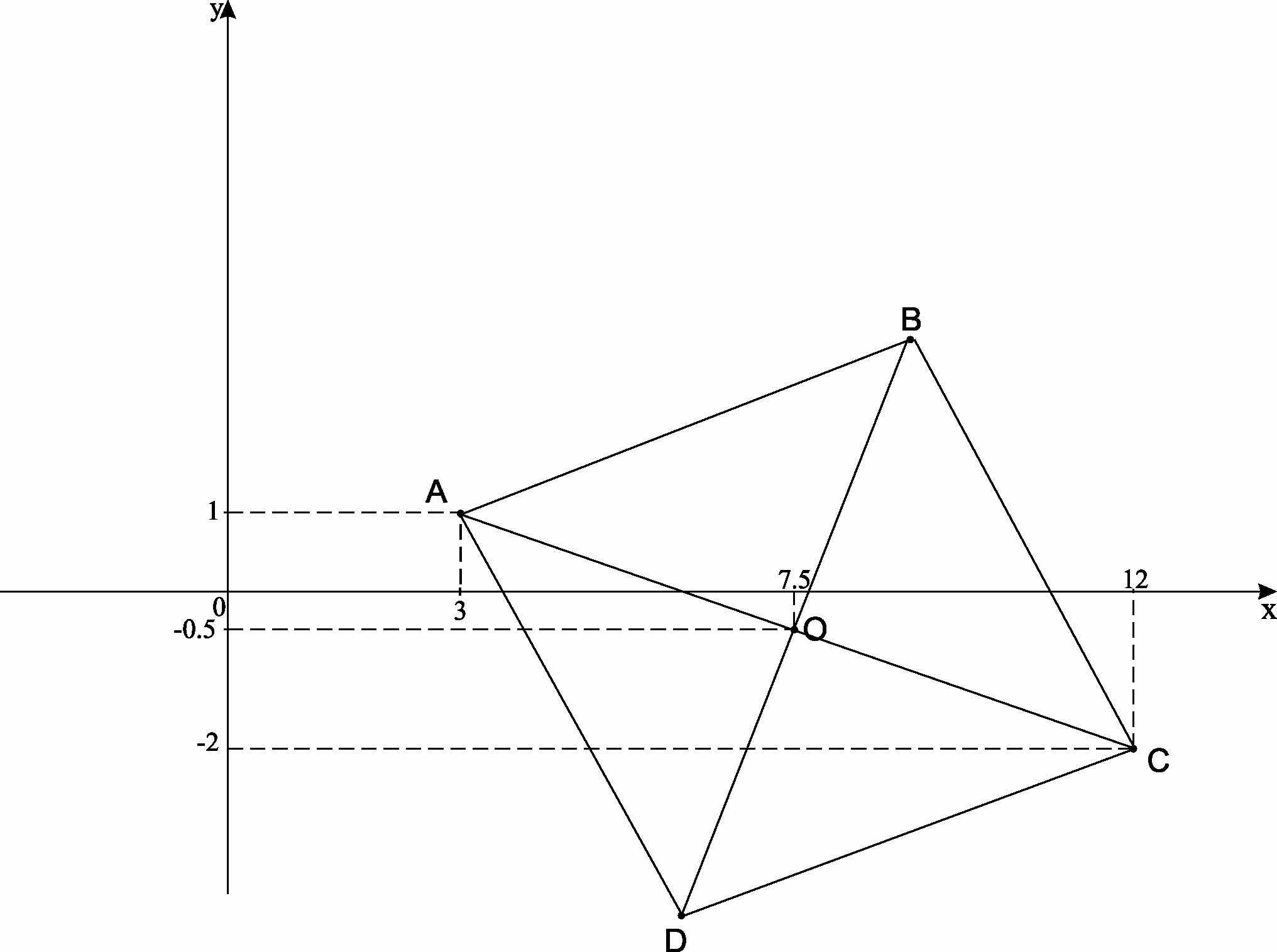
Сделать чертеж.
.
Найти уравнение второй диагонали.
Сделать чертеж.
Решение.
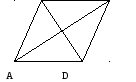
Пусть
![]() - уравнение стороныАВ.
Так как прямые
- уравнение стороныАВ.
Так как прямые
![]() и
и![]() имеют одинаковые нормальные векторы
имеют одинаковые нормальные векторы![]() ,
следовательно, они параллельны. Поэтому
,
следовательно, они параллельны. Поэтому![]() - уравнение противоположной стороныDC.
Одна из диагоналей, например, АС
имеет уравнение
- уравнение противоположной стороныDC.
Одна из диагоналей, например, АС
имеет уравнение
![]() .
Вершина ромбаA
является точкой пересечения прямых АВ
и АС,
следовательно ее можно найти, решив
систему уравнений:
.
Вершина ромбаA
является точкой пересечения прямых АВ
и АС,
следовательно ее можно найти, решив
систему уравнений:
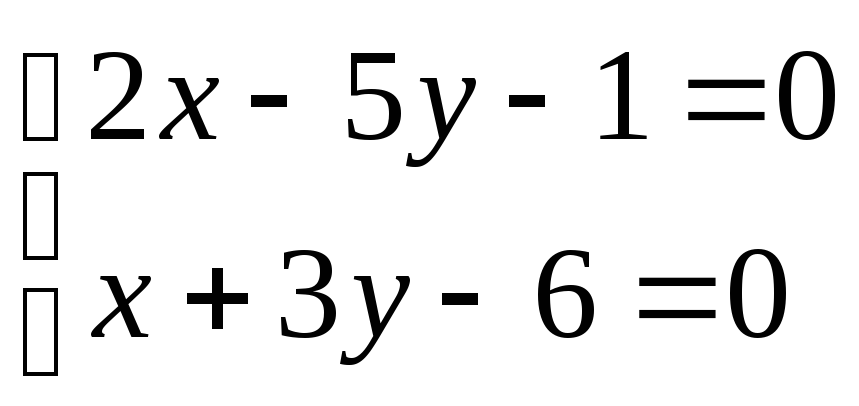 ,
откуда А(3;1).
,
откуда А(3;1).
Вершину ромба С получим решением системы, составленной из уравнения прямых DC и АС:
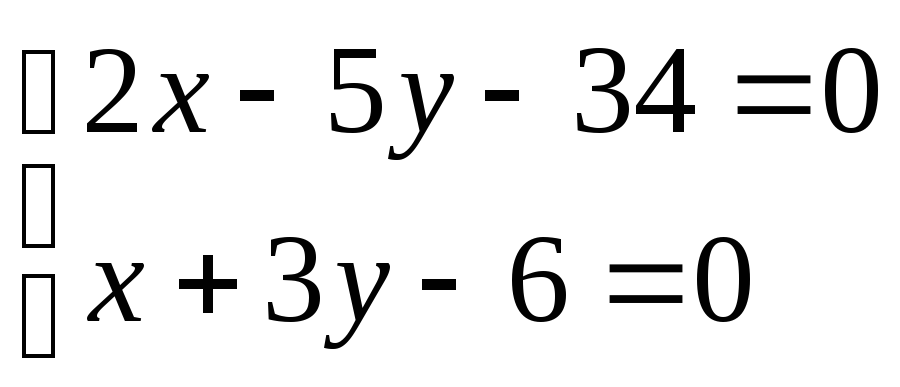 ,
откуда С(12;-2).
,
откуда С(12;-2).
Точка О пересечения диагоналей является серединой отрезка АС, поэтому ее координаты можно найти по формулам:
![]() .
Таким образом
.
Таким образом
![]() .
.
Так как диагонали
ромба перпендикулярны, то угловой
коэффициент искомой диагонали
![]() .
Угловой коэффициент прямойАС
.
Угловой коэффициент прямойАС
![]() ,
найдем из ее уравнения:
,
найдем из ее уравнения:![]() ,
откуда
,
откуда![]() .
Следовательно,
.
Следовательно,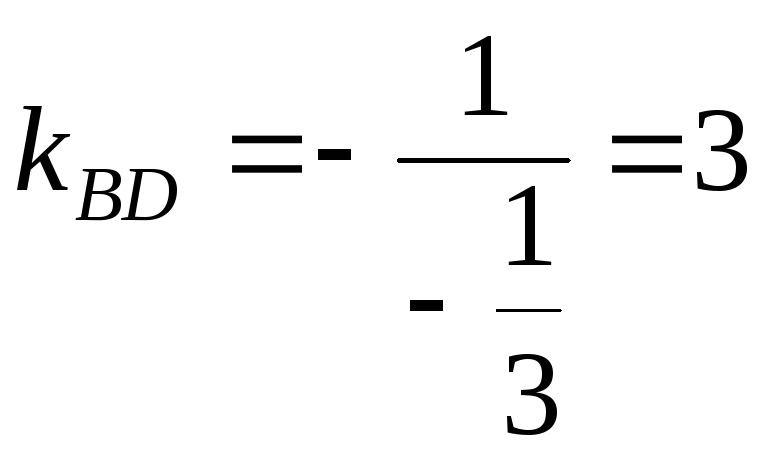 .
.
Уравнение диагонали
BD
найдем, зная угловой коэффициент
![]() и точку
и точку![]() ,
лежащую на ней:
,
лежащую на ней:![]() ,
т.е.
,
т.е.![]() или
или![]() .
.
Ответ:
![]() .
.
Выполним чертеж:
Решения заданий типа 41-50.
Теоретический справочник
При вычислении пределов используются следующие свойства пределов:
![]() ,
где
,
где
![]() ,
т.е. предел постоянной равен самой
постоянной.
,
т.е. предел постоянной равен самой
постоянной.
![]() ,
то
,
то
а)
![]()
![]()
![]() ;
;
б)
![]()
![]()
![]() ;
;
в)
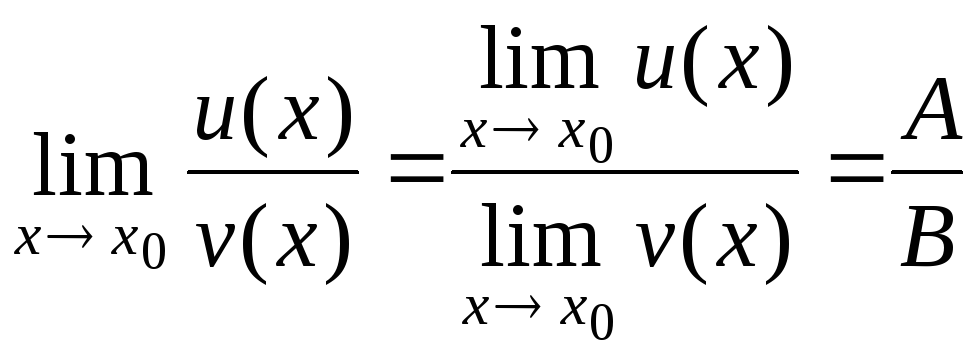 ,
если
,
если![]() .
.
Из свойств 10
и
![]() следует,
что
следует,
что
![]()
![]() ,где
,где
![]() ,
т.е. постоянную можно выносить за знак
предела.
,
т.е. постоянную можно выносить за знак
предела.
![]() Если
Если
![]() ,
то
,
то![]() .
.
![]() Если
Если
![]() ,
то
,
то![]() .
.
![]()
![]()
![]() .
.
![]() Для всех элементарных
функций
Для всех элементарных
функций
![]() в любой точке их области определения
имеет место равенство:
в любой точке их области определения
имеет место равенство:![]() ,
т.е. предел функции находят непосредственной
подстановкой предельного значения
аргумента.
,
т.е. предел функции находят непосредственной
подстановкой предельного значения
аргумента.
Из свойства
![]() следует, что предел суммы, произведения,
частного двух функций равен, соответственно,
сумме, произведению и частному пределов
этих функций, если функции имеют конечные
пределы (в случае частного предел
знаменателя не равен нулю). Если
следует, что предел суммы, произведения,
частного двух функций равен, соответственно,
сумме, произведению и частному пределов
этих функций, если функции имеют конечные
пределы (в случае частного предел
знаменателя не равен нулю). Если![]()
![]() ,
то
,
то![]() приводит к неопределенности типа
приводит к неопределенности типа![]() ;
если
;
если![]()
![]() ,
то
,
то![]() приводит к неопределенности типа
приводит к неопределенности типа![]() ;
если
;
если![]()
![]() ,
то
,
то![]() приводит к неопределенности типа
приводит к неопределенности типа![]() .
Чтобы вычислить такие пределы, т.е.
«раскрыть неопределенность», необходимо
провести дополнительные преобразования.
.
Чтобы вычислить такие пределы, т.е.
«раскрыть неопределенность», необходимо
провести дополнительные преобразования.
Пример 1. Вычислить
предел
![]() .
.
Числитель и
знаменатель дроби являются многочленами
и при
![]() стремятся к бесконечности и, следовательно,
имеем неопределенность
стремятся к бесконечности и, следовательно,
имеем неопределенность![]() .
Для раскрытия такой неопределенности
вынесем в числителе и знаменателе
.
Для раскрытия такой неопределенности
вынесем в числителе и знаменателе![]() .
.
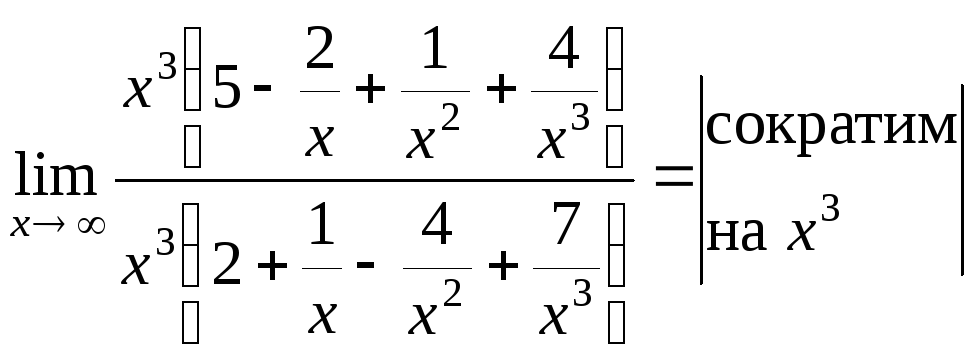 =
=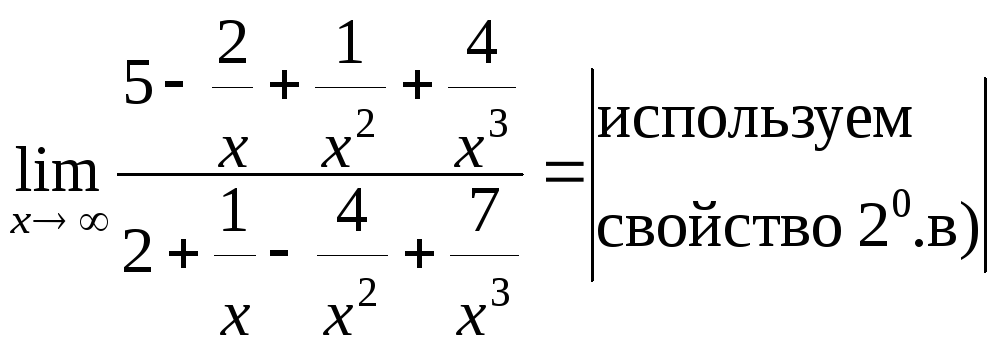 =
=
=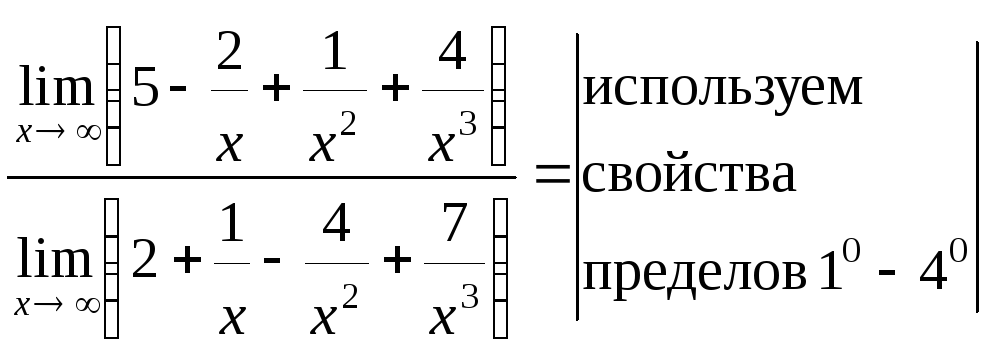 =
=
=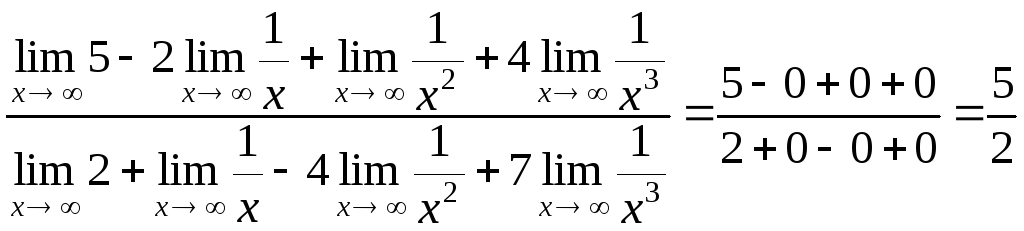 .
.
Рассмотрим случай, когда многочлен, стоящий в числителе имеет меньшую степень по сравнению с многочленом, стоящим в знаменателе:
![]()
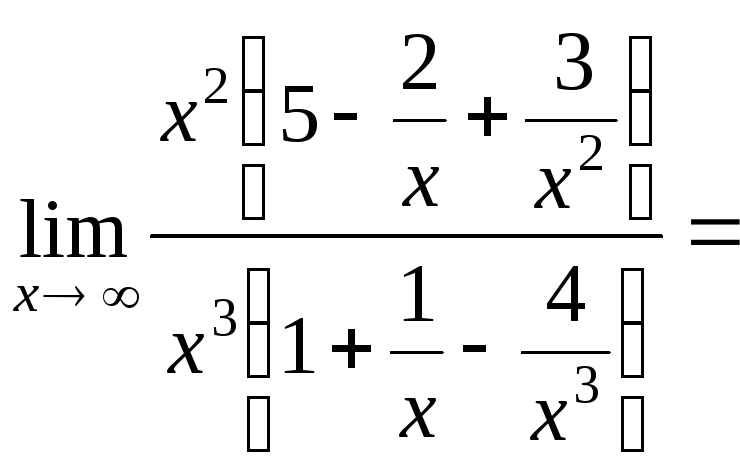
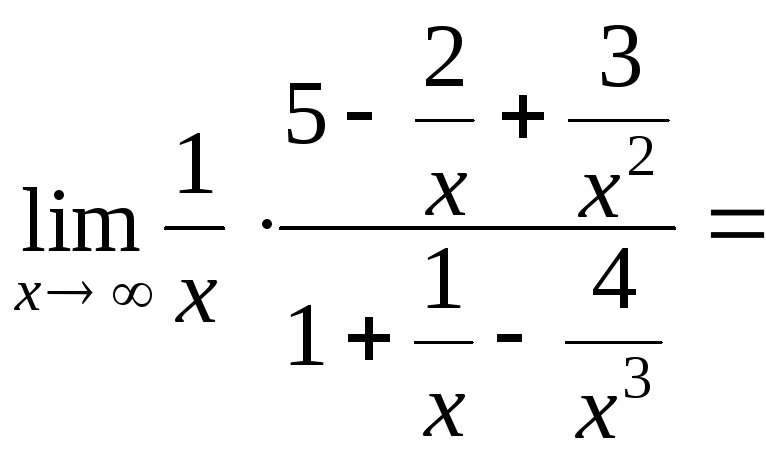
=
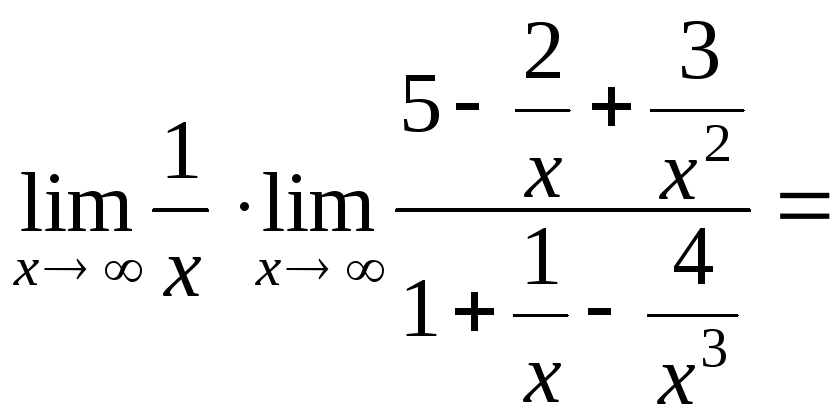
![]() .
.
Рассмотрим случай, когда многочлен, стоящий в числителе имеет большую степень по сравнению с многочленом, стоящим в знаменателе:
![]()
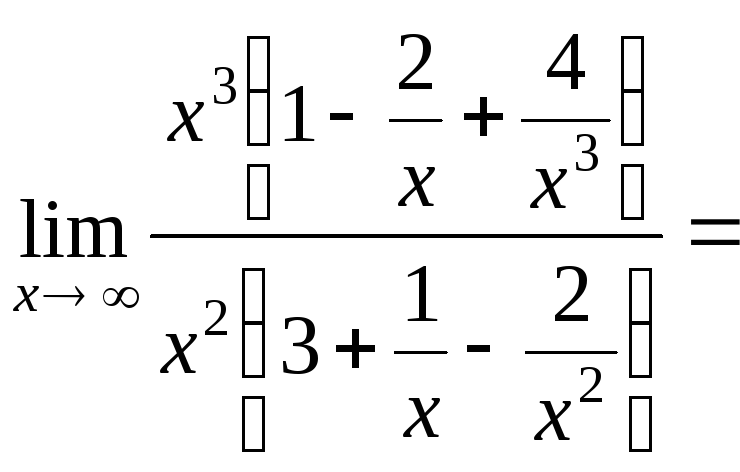
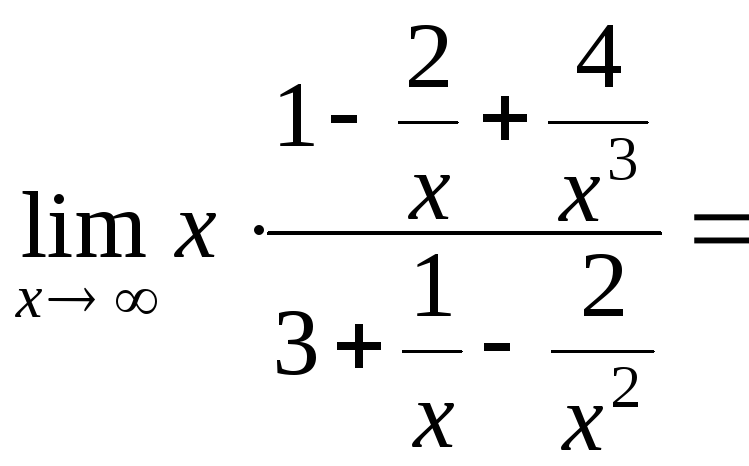
=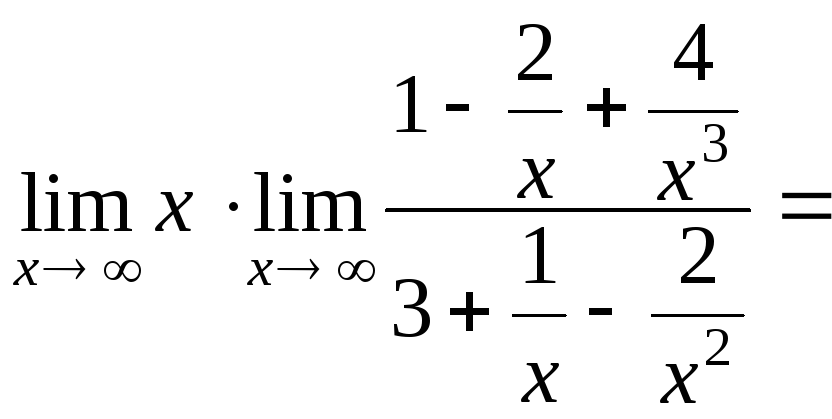
![]()
![]() .
.
Пример 2. Вычислить
![]() .
.
Определим, имеет
ли место неопределенность. Для этого в
выражение, стоящее под пределом подставим
![]() .
Т.о. имеем неопределенность
.
Т.о. имеем неопределенность![]() .
Разложим на множители числитель:
.
Разложим на множители числитель:![]()
=
![]() ,
знаменатель:
,
знаменатель:![]() и подставим это в предел
и подставим это в предел![]() =
=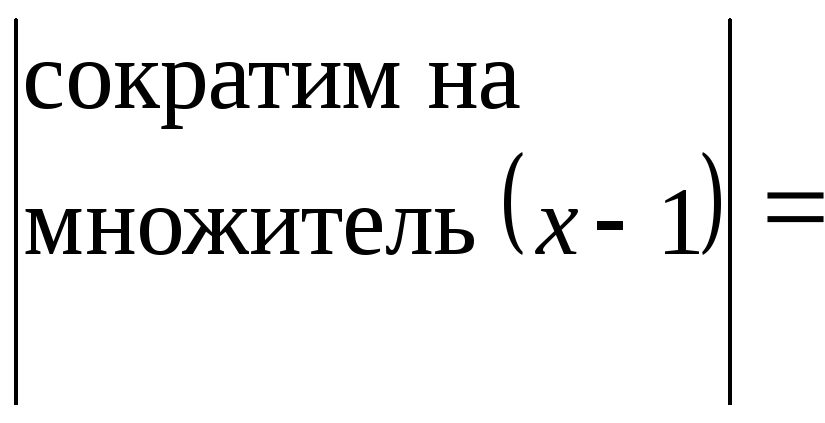
=![]() =
=![]() .
.
Пример 3. Вычислить
![]() .
.
![]() =
=![]() .
Домножим числитель и знаменатель на
выражение сопряженное числителю:
.
Домножим числитель и знаменатель на
выражение сопряженное числителю:![]() .
.
![]()
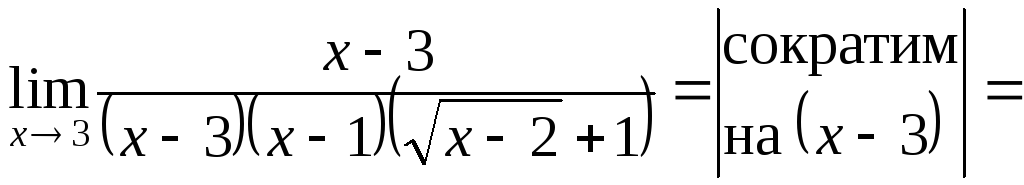
=![]()
![]()
![]()
![]() .
.
Если при раскрытии
неопределенности
![]() ,
дробь содержит тригонометрические
функции, то в этом случае используют
первый замечательный предел:
,
дробь содержит тригонометрические
функции, то в этом случае используют
первый замечательный предел:![]() .
.
Пример 4. Вычислить
![]() .
.
![]() =
=![]() .
Преобразуем выражение
.
Преобразуем выражение
![]() =
=![]() .
Отдельно вычислим:
.
Отдельно вычислим:![]() =
=
=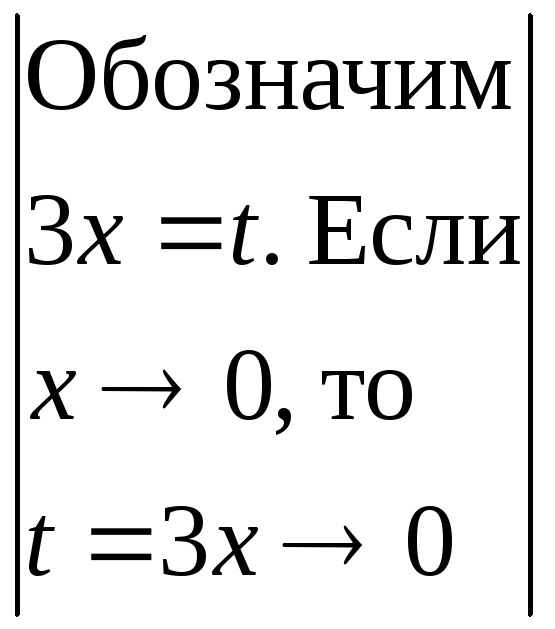 =
=![]() .
Аналогично,
.
Аналогично,![]() =
=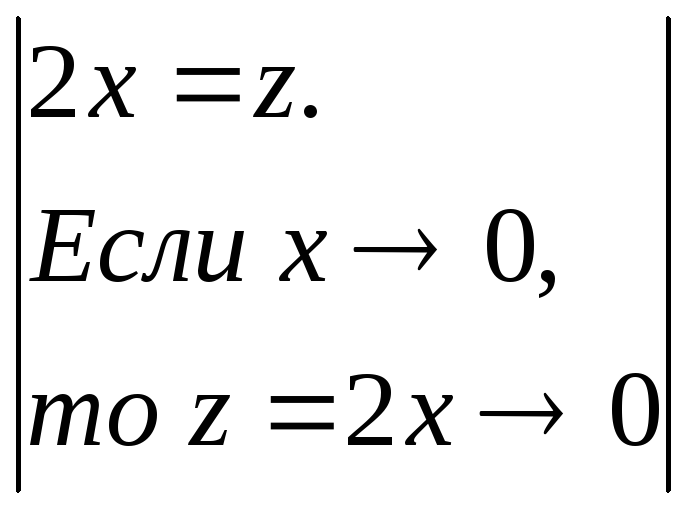 =
=
=![]() =
=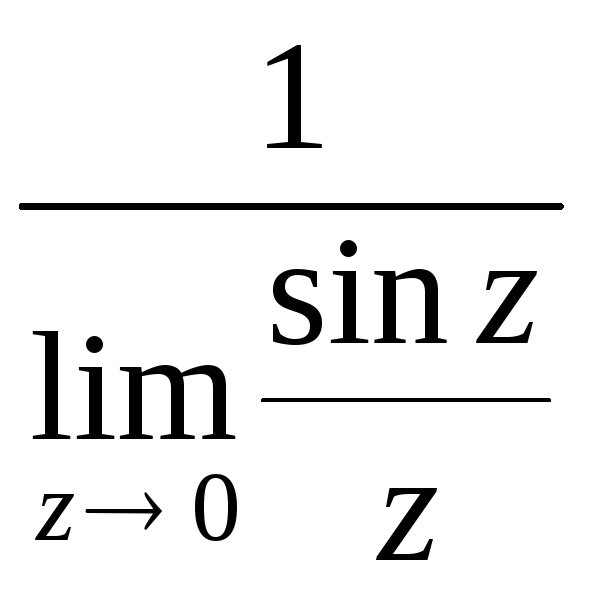 =
=![]() .
.
![]() .
.
Следовательно,
![]() =
=![]() =
=![]() .
.
Пример 5.
![]()
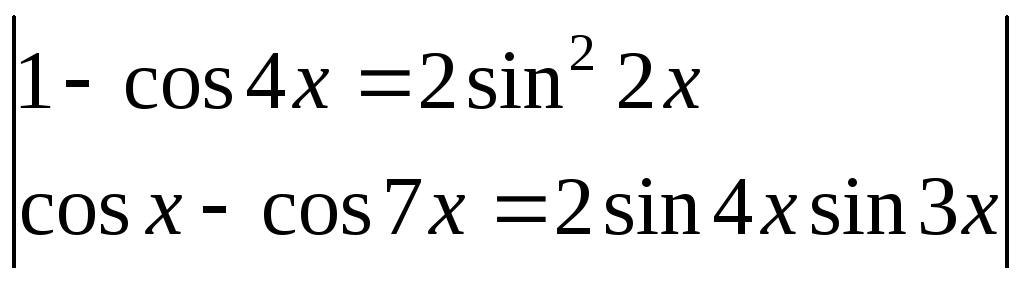 =
=![]() =
=
=![]() =
=![]() =
=
=![]() .
.
При раскрытии
неопределенности
![]() используют второй замечательный предел:
используют второй замечательный предел:![]() или
или![]() .
.
Пример 6. Вычислить
![]() .
.
Вычислим отдельно
предел основания
![]() =
=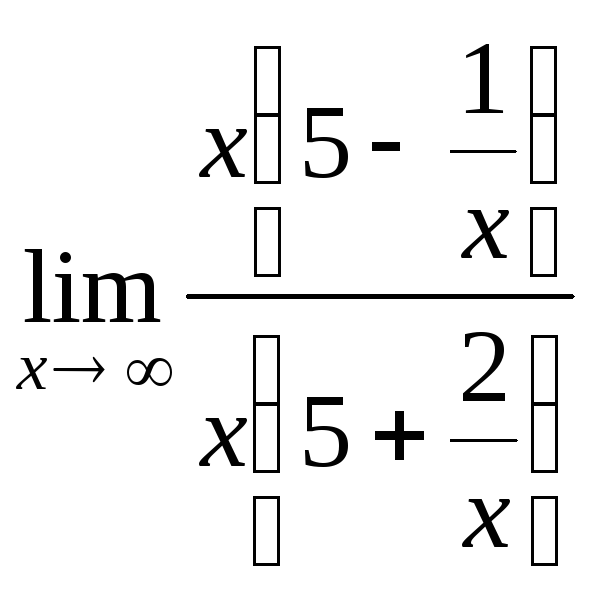 =
=
=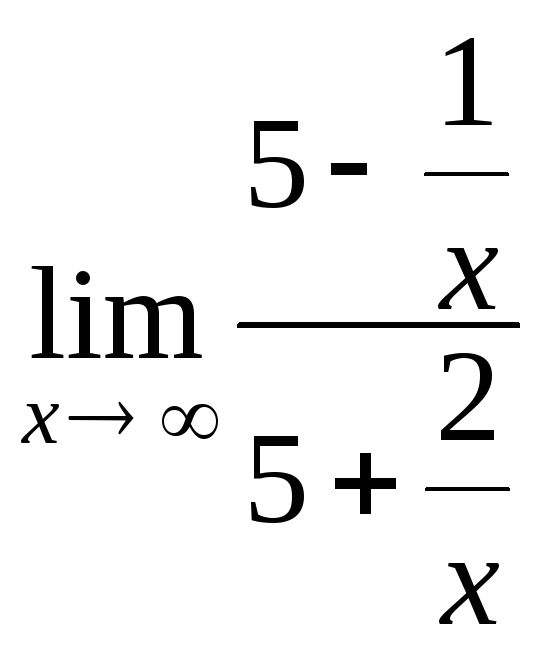 =
=![]() и предел показателя
и предел показателя![]() ,
получаем неопределенность
,
получаем неопределенность![]() .
.
Преобразуем
выражение в скобках к виду
![]()
![]() ,
т.е.
,
т.е.
![]() .
Из второго замечательного предела
следует, что
.
Из второго замечательного предела
следует, что![]() ,
поэтому преобразуем показатель степени
так, чтобы он содержал сомножитель
,
поэтому преобразуем показатель степени
так, чтобы он содержал сомножитель![]() Таким образом
Таким образом![]() =
=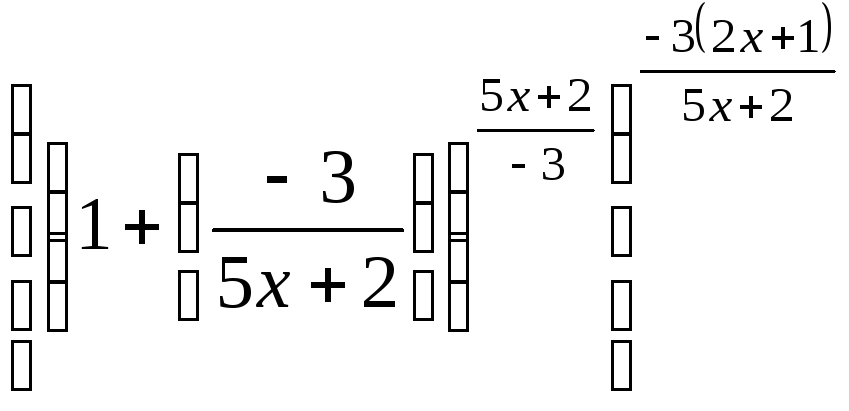 .
Тогда
.
Тогда![]()
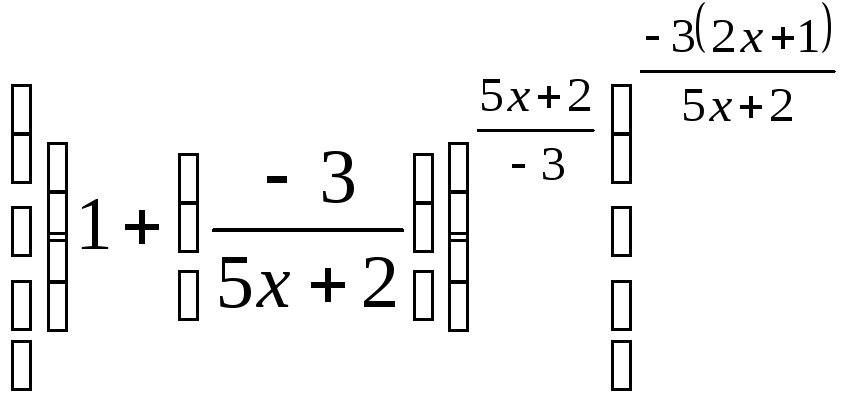 =
=![]() =
=![]() =
=
=![]() =
=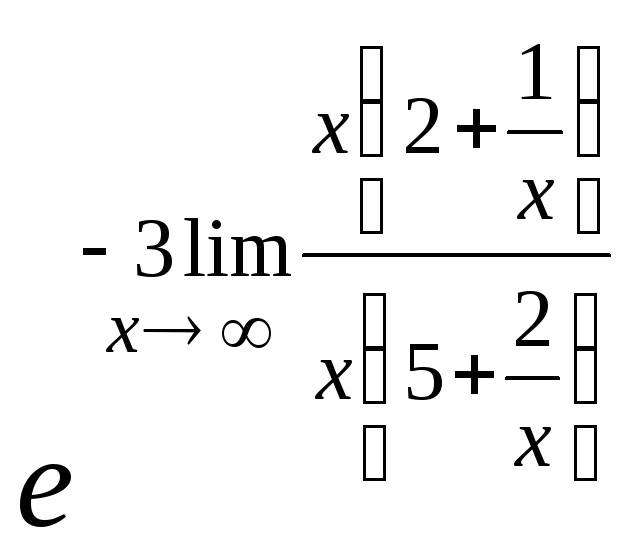 =
=![]() .
.
Пример 7. Вычислить
![]() .
.
Выражение в скобках
запишем в виде
![]() т.е.
т.е.
![]() .
Следовательно, показатель степени
должен содержать сомножитель
.
Следовательно, показатель степени
должен содержать сомножитель
![]() :
:
![]()
![]() =
=![]() =
=
=![]() =
=![]() .
.
Для раскрытия
неопределенностей типа
![]() или
или![]() удобно использовать правило
Лопиталя-Бернулли:
удобно использовать правило
Лопиталя-Бернулли:![]() ,
т.е. предел отношения функций в случае
неопределенности
,
т.е. предел отношения функций в случае
неопределенности![]() или
или![]() равен пределу отношения производных
этих функций.
равен пределу отношения производных
этих функций.
Для применения правила Лопиталя-Бернулли необходимо научиться вычислять производные функций.
Пример 8. Вычислить
![]() .
.
![]() =
=![]()
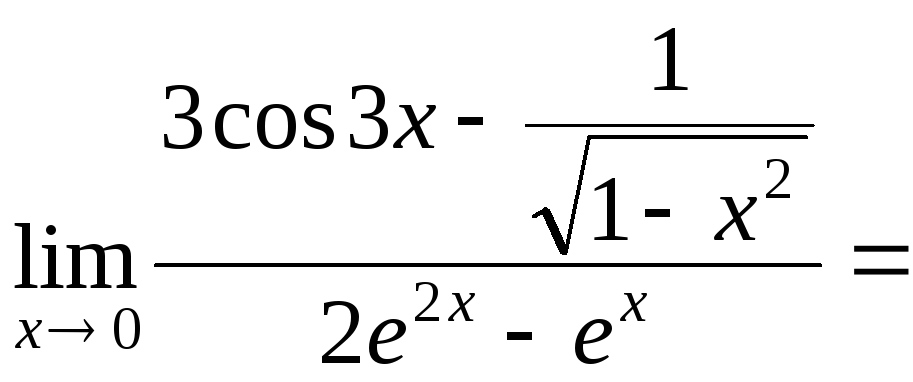
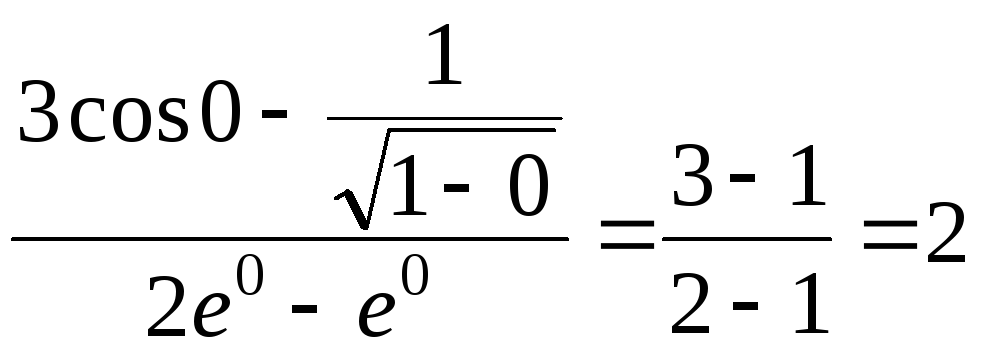 .
.
Правило Лопиталя-Бернулли при вычислении предела можно применять несколько раз.
Пример 9. Вычислить
![]() .
.
![]() =
=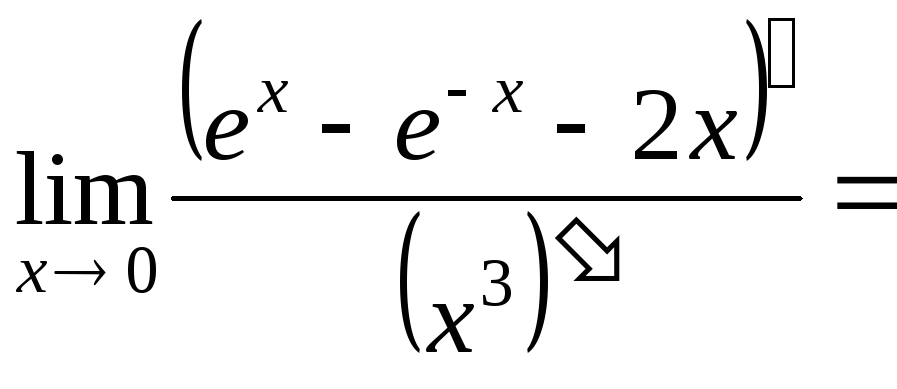
![]() =
=
=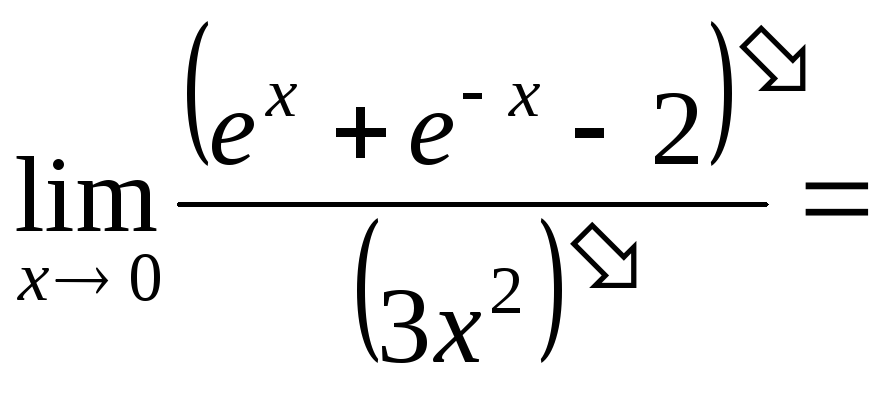
![]() =
=![]()
![]()
![]() .
.
Решения заданий типа 51-60.
Теоретический справочник
Дифференцированием
функции
![]() называют нахождение ее производной
называют нахождение ее производной![]() ,
которое выполняется с помощью правил
дифференцирования и таблицы производных
основных элементарных функций.
,
которое выполняется с помощью правил
дифференцирования и таблицы производных
основных элементарных функций.
Правила дифференцирования
10.
![]() ,
гдес
– постоянная;
,
гдес
– постоянная;
20.
![]() ;
;
Если
![]() – некоторые дифференцируемые функции,
то:
– некоторые дифференцируемые функции,
то:
30.
![]() ;
;
40.
![]() ;
;
50.
![]() ;
;
60.
![]() ;
;
70.
Если
![]() сложная функция, то:
сложная функция, то:![]() или
или![]() .
.
Таблица производных основных элементарных функций
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.![]()
10.![]()
11.![]()
12.![]()
13.
![]() .
.
Пример 1. Найти
производную
![]() функции
функции![]() .
.
Решение. Заменяя
корни степенями с дробными показателями,
получаем
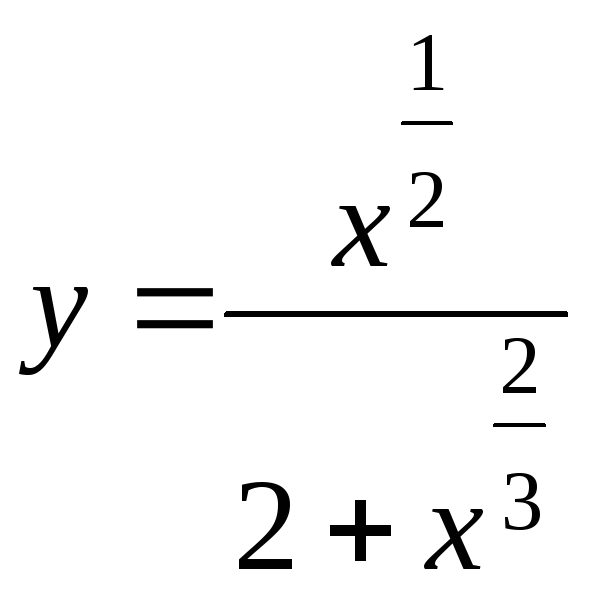 .
По правилу дифференцирования дроби
(60)
и суммы (30)
имеем
.
По правилу дифференцирования дроби
(60)
и суммы (30)
имеем
![]() =
=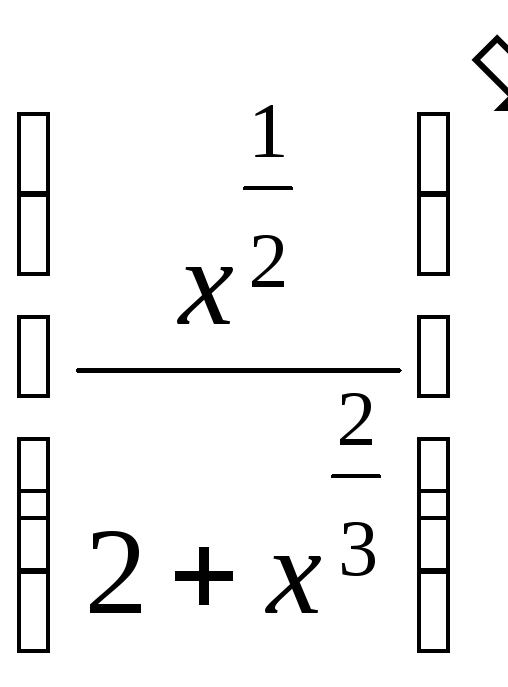 =
=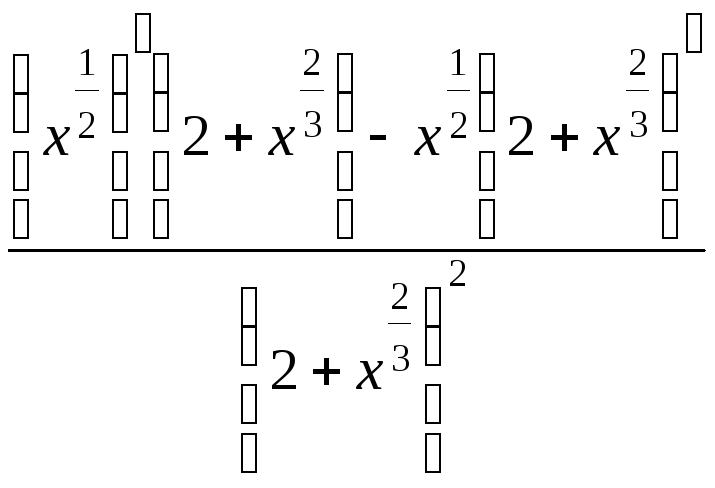 =
=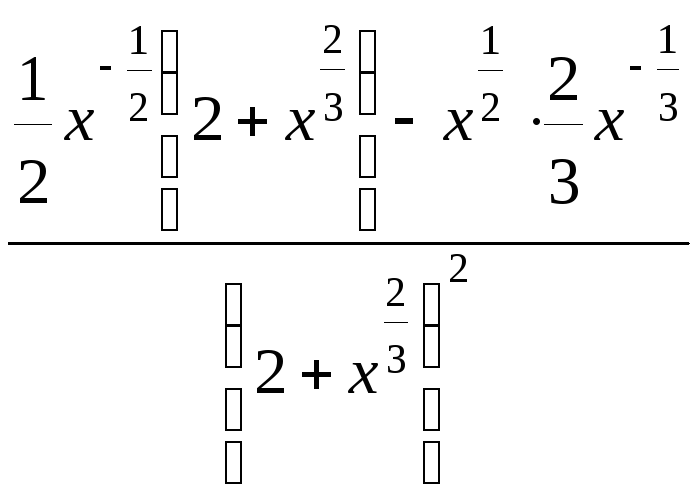 =
=
=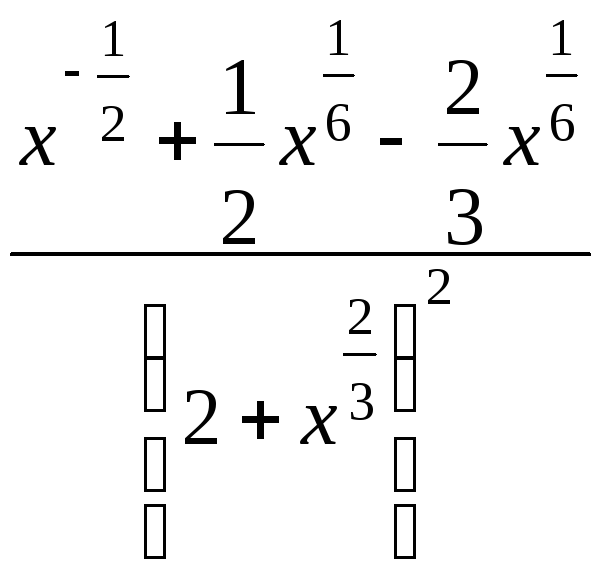 =
= =
=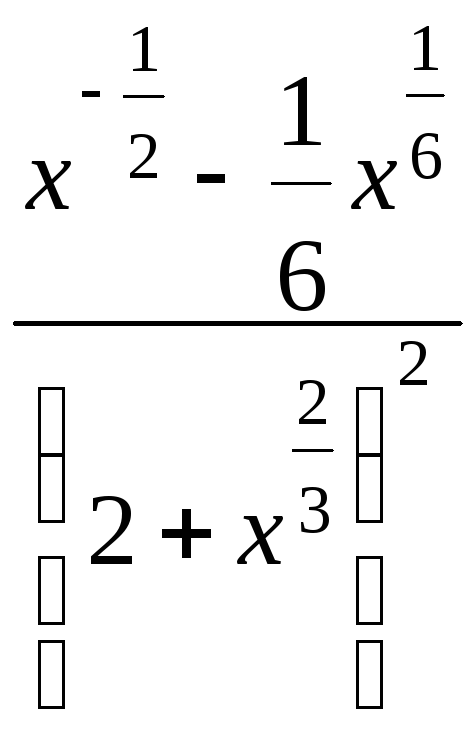 =
= =
=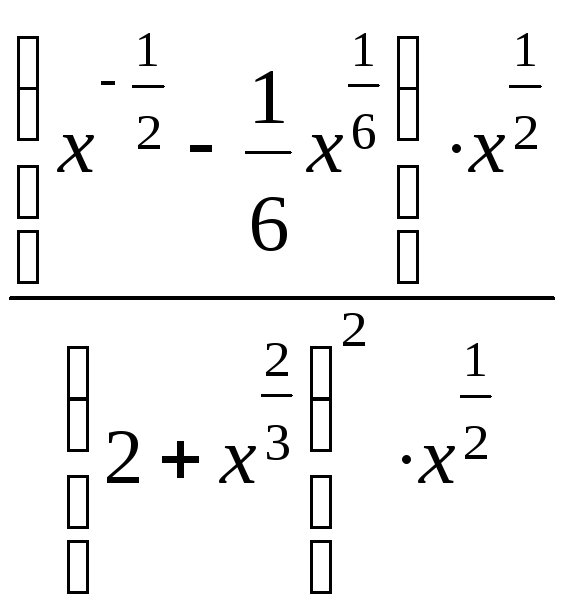 =
=
=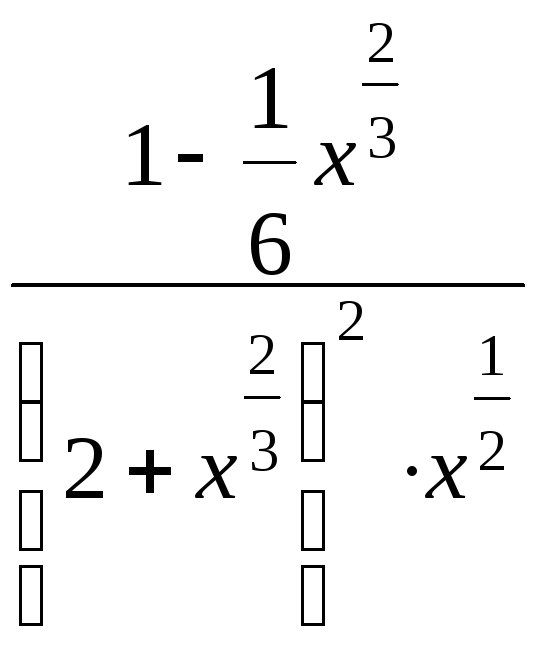 =
=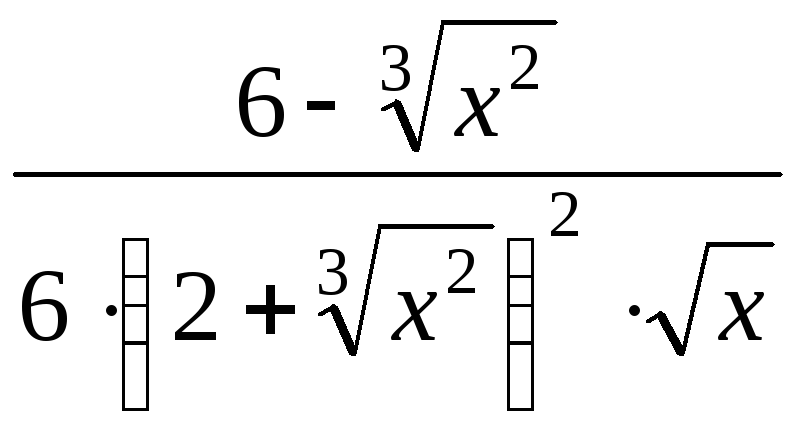 .
.
Пример 2. Найти
производную
![]() функции
функции![]() .
.
Решение. По правилу дифференцирования дроби (60), используя табличные формулы (6,7) и применяя правило дифференцирования сложной функции (70), получим
![]() =
=![]() =
=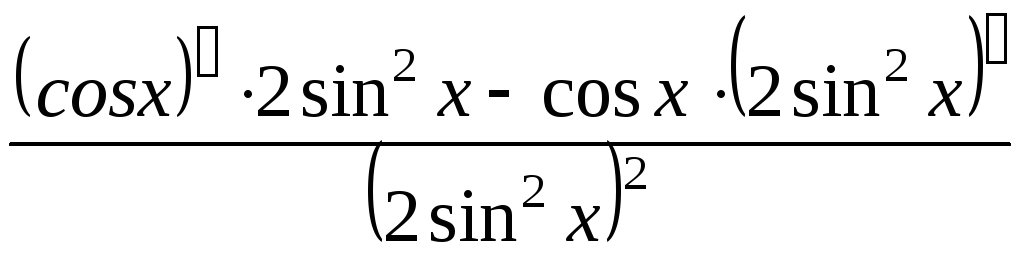 =
=
=![]() =
=![]() =
=
=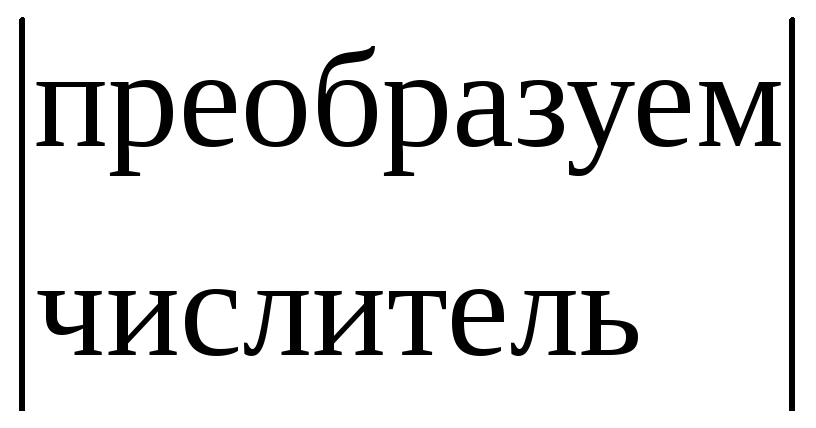 =
=![]() =
= =
=![]() =
=
=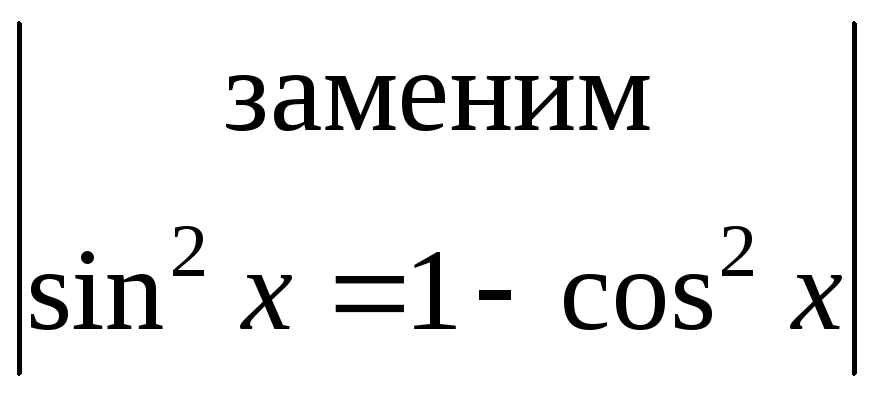 =
=![]() .
.
Пример 3. Найти
производную
![]() функции
функции![]() .
.
Решение. Используя правило дифференцирования произведения (40), правило дифференцирования сложной функции (70) и табличные формулы (1, 12), получим
![]() =
=
=![]() =
=
=![]() =
=![]() =
=
=![]() .
.
Пример 4. Найти
производную
![]() функции
функции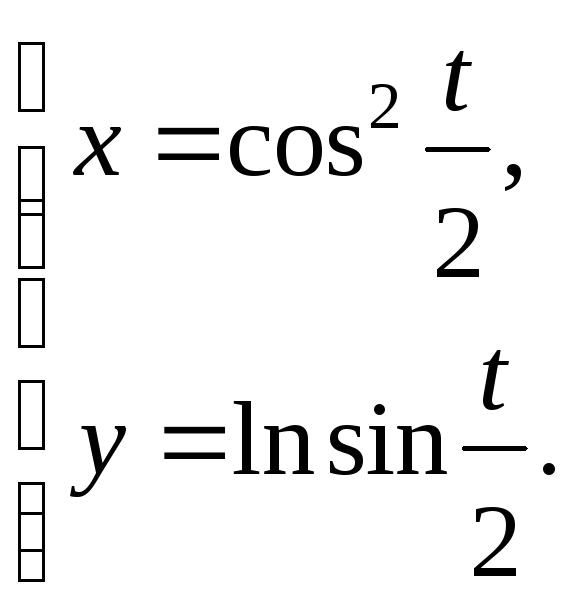
Решение. В этом
примере функция задана параметрическими
уравнениями
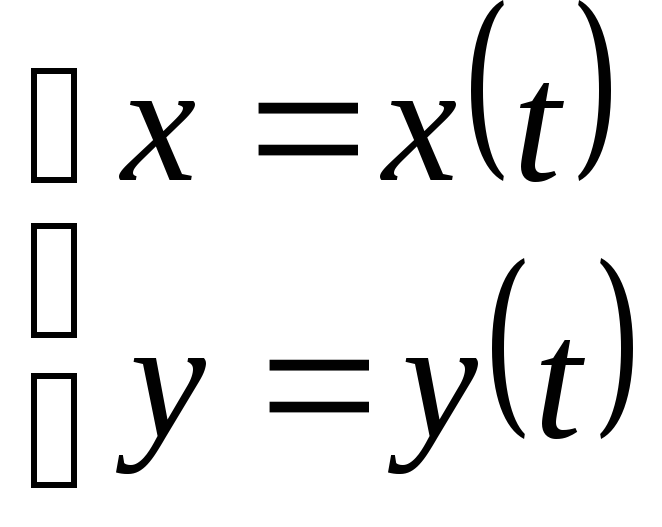 ,
причем функции
,
причем функции![]() и
и![]() дифференцируемы и
дифференцируемы и![]() ,
тогда по правилу дифференцирования
функции, заданной параметрически имеем
,
тогда по правилу дифференцирования
функции, заданной параметрически имеем![]() или
или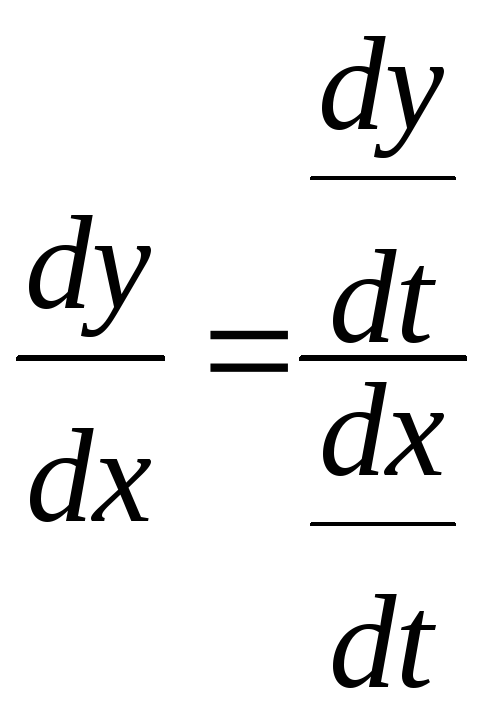 .
Следовательно, нужно найти производные
отх
и у
по параметру t:
.
Следовательно, нужно найти производные
отх
и у
по параметру t:
![]() =
=![]() =
=
=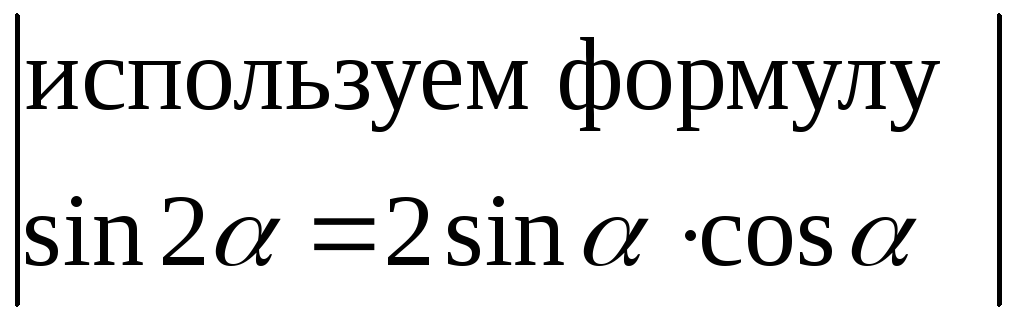 =
=![]() ;
;
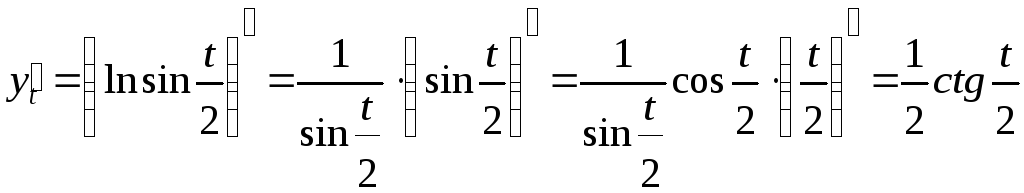 .
.
Отсюда
![]()
![]() =
=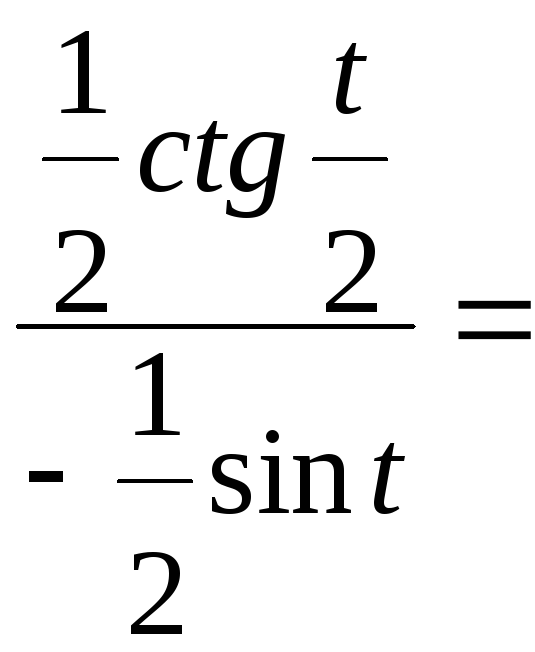
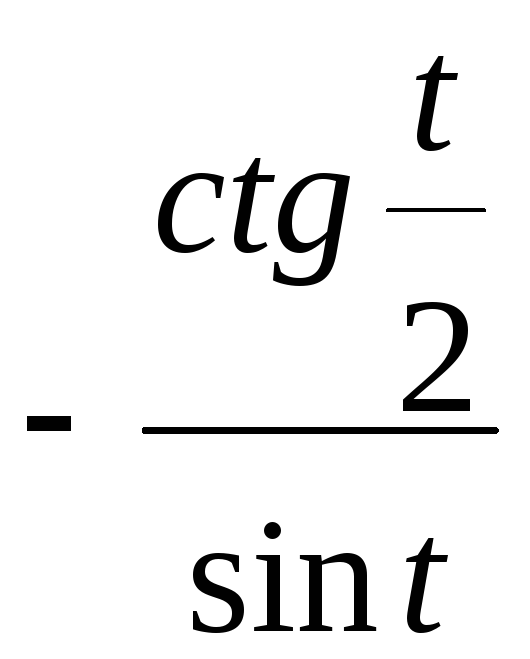 ;
;
Ответ:
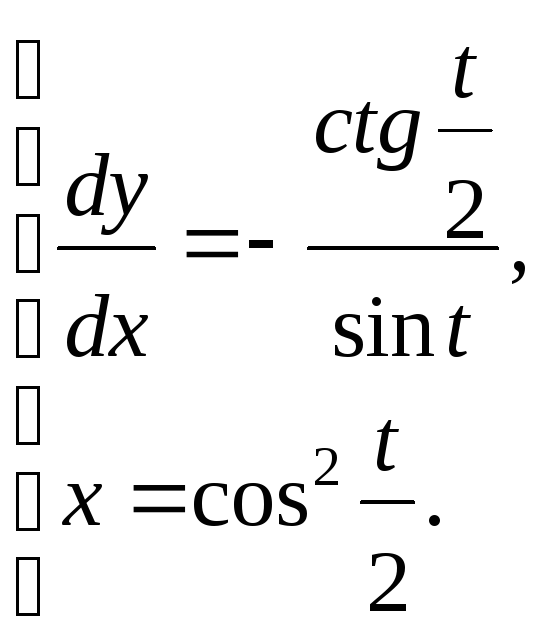
Решение задания типа 61-70.
Исследовать
методами дифференциального исчисления
функцию
![]() и, используя результаты исследования,
построить ее график.
и, используя результаты исследования,
построить ее график.
Решение. Исследование функций и построение их графиков проводится по следующей схеме:
найти область определения функции
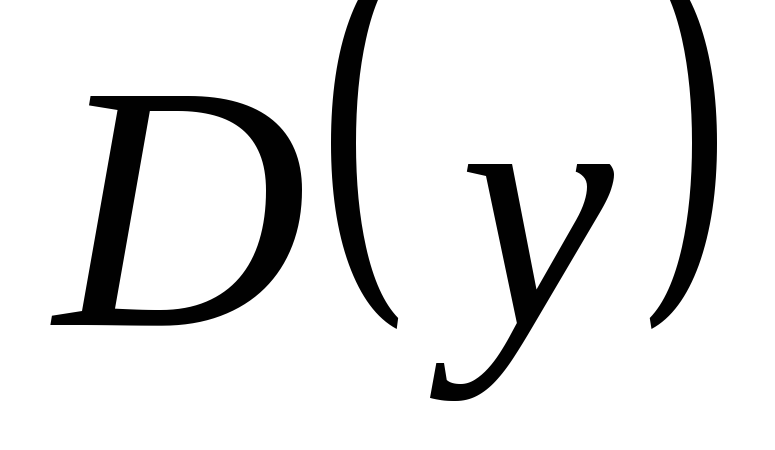 ;
исследовать функцию на четность и
нечетность;
;
исследовать функцию на четность и
нечетность;исследовать функцию на непрерывность; найти точки разрыва (если они существуют) и установить характер разрыва;
найти асимптоты графика функции;
найти интервалы возрастания и убывания функции и ее экстремумы;
найти интервалы выпуклости и вогнутости графика функции и точки перегиба;
найти точки пересечения графика функции с осями координат;
построить график функции.
1) Область определения
функции:
![]() =
=![]() .
Проверим функцию на четность, нечетность:
.
Проверим функцию на четность, нечетность:![]() =
=![]()
![]()
![]() .
Значит функция ни четная, ни нечетная.
.
Значит функция ни четная, ни нечетная.
2) Точка разрыва х
= 2, причем
![]() ,
,![]() ,
следовательно,х
= 2 является вертикальной асимптотой
графика функции.
,
следовательно,х
= 2 является вертикальной асимптотой
графика функции.
3) Найдем наклонные
асимптоты
![]() ,
для этого вычислим
,
для этого вычислим![]() =
=![]()
![]() ;
;
![]() =
=![]() .
.
Таким образом,
прямая
![]() является наклонной асимптотой графика
функции.
является наклонной асимптотой графика
функции.
4) Интервалы возрастания, убывания и экстремумы определим по следующей схеме:
а) находим первую
производную
![]() ;
;
б) находим критические
точки, т.е. точки, в которых
![]() =0
или
=0
или![]() не существует;
не существует;
в) область определения
разбиваем критическими точками на
конечное число интервалов монотонности,
в каждом из которых
![]() имеет строго определенный знак;
имеет строго определенный знак;
г) в соответствии с достаточными условиями определяем интервалы возрастания, убывания функции и ее экстремумы.
Итак,
а)
![]() =
=
=![]() .
.
б) критические
точки находим из уравнения
![]() .
Отсюда
.
Отсюда![]() ,
следовательно,
,
следовательно,![]()
в) область определения разбиваем критическими точками на интервалы монотонности следующим образом:

г) вычисляем экстремумы функции:
![]() ;
;
![]() .
.
5) Найдем интервалы
выпуклости, вогнутости кривой и ее точки
перегиба. Вычислим
![]() :
:
![]() =
=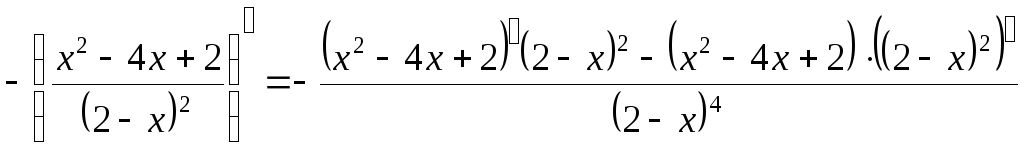 =
=
=![]() =
=
=![]() ;
;
Найдем точки, в
которых
![]() =0
или
=0
или![]() не существует:
не существует:
![]() =
=![]() - нет решений,
- нет решений,![]() не существует, если
не существует, если![]() ,
откуда
,
откуда![]() .
.
Находим интервалы
знакопостоянства для
![]() :
:

Так как
![]() не входит в
не входит в![]() ,
то точек перегиба графика нет.
,
то точек перегиба графика нет.
6) Найдем точки
пересечения графика с осями координат:
если
![]() ,
то
,
то![]() ,
если
,
если![]() ,
то
,
то![]() или
или![]() и
и![]() .
Следовательно, график проходит через
точки
.
Следовательно, график проходит через
точки![]() .
.
7) Используя полученные результаты исследования, строим график функции.
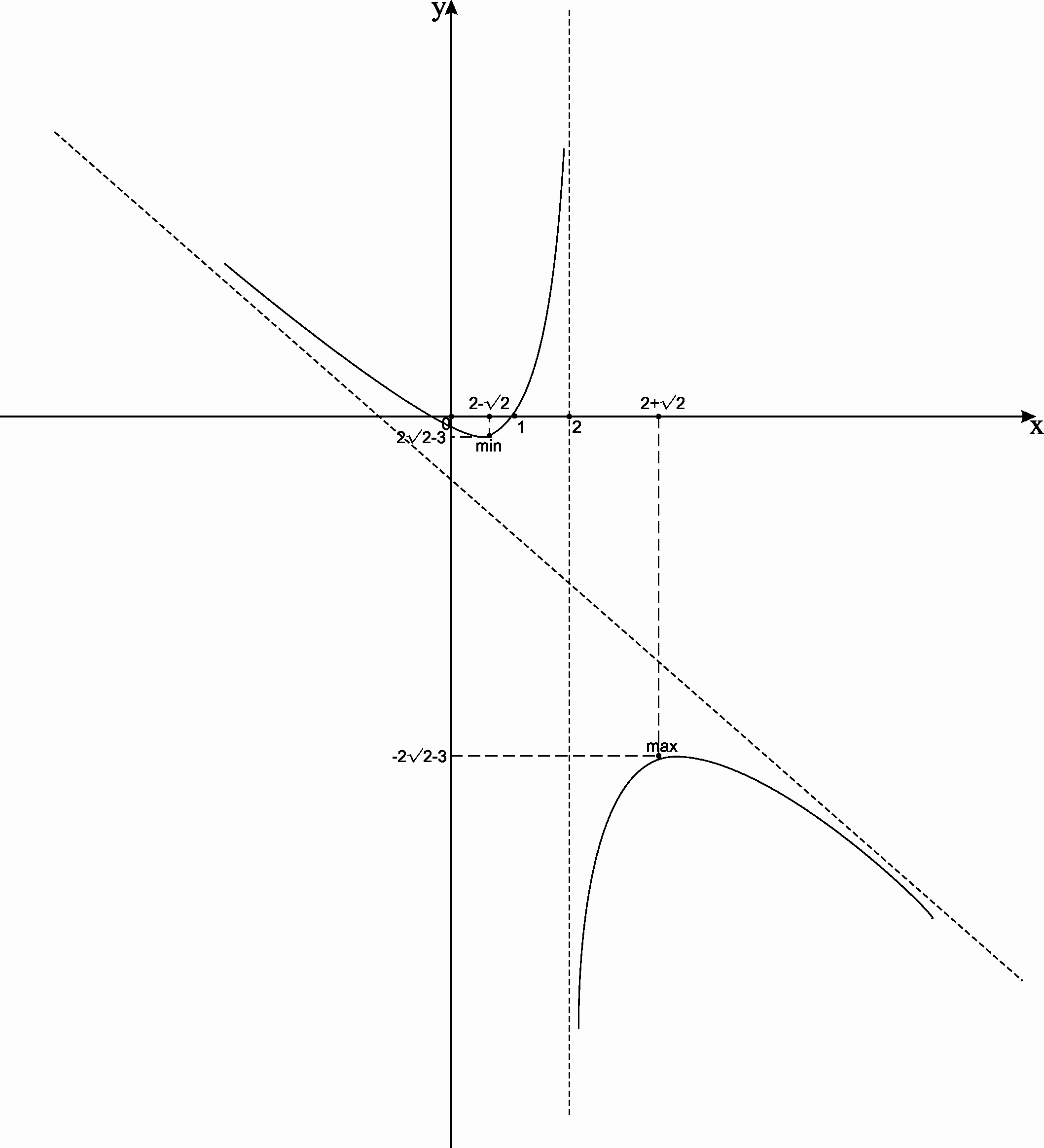
Методические указания для выполнения контрольной работы № 2.
Решение заданий
типа 71-80. Даны
функция трех переменных
![]() ,
точка
,
точка![]() и вектор
и вектор![]() .
Найти: 1) градиент функции
.
Найти: 1) градиент функции![]() в точке
в точке![]() ;
2) производную функции
;
2) производную функции![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() .
.
Например,
![]() ,
,![]() ,
,![]() .
.
Решение. 1) Градиент
функции
![]() в точке
в точке![]() это
вектор, равный:
это
вектор, равный:
![]() ,
где
,
где
![]() значения частных производных функции
значения частных производных функции![]() по переменнымx,y,z,
соответственно, в точке М0.
по переменнымx,y,z,
соответственно, в точке М0.
Найдем частные
производные функции
![]() .
Частная производная по переменнойх
является обыкновенной производной
функции одной переменной х
при фиксированном значении переменных
у
и z
и обозначается
.
Частная производная по переменнойх
является обыкновенной производной
функции одной переменной х
при фиксированном значении переменных
у
и z
и обозначается
![]() .
Т.о.
.
Т.о.![]() =
=![]() .
.
При вычислении
![]() (частной производной по переменнойу)
переменные х
и z
считают постоянными. Тогда
(частной производной по переменнойу)
переменные х
и z
считают постоянными. Тогда
![]() =
=![]() =
=![]() =
=![]() .
.
При вычислении
![]() (частной производной по переменнойz)
переменные х
и y
считают постоянными. Тогда
(частной производной по переменнойz)
переменные х
и y
считают постоянными. Тогда
![]() =
=![]()
=![]() =
=![]() .
.
Вычислим значения
частных производных в точке
![]() :
:
![]() =
=![]() ;
;![]() =
=![]() ;
;![]() =
=![]() .
.
Тогда
![]() .
.
2) Производная
функции
![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() вычисляется по формуле
вычисляется по формуле
![]() =
=![]() ,
,
где
![]() =3,
=3,![]() ,
,![]() вычислены
в предыдущем задании этой задачи, а
вычислены
в предыдущем задании этой задачи, а![]() направляющие
косинусы вектора
направляющие
косинусы вектора![]() ,
которые вычисляются по формулам
,
которые вычисляются по формулам![]() ,
,![]() ,
,![]() .
Для вектора
.
Для вектора![]() они равны
они равны![]() ;
;![]() ;
;![]() .
Тогда производная функции по направлению
вектора
.
Тогда производная функции по направлению
вектора![]() в точке
в точке![]() равна
равна
![]() .
.
Решения заданий
типа 81-90. Производятся
два вида товаров, объемы производства
которых х
и у,
цены на эти товары
![]() и
и![]() ,
соответственно, затраты на производство
задаются функцией издержек
,
соответственно, затраты на производство
задаются функцией издержек![]() .
Определить при каких объемах производства
данных товаров прибыль будет максимальной;
найти ее максимальное значение.
.
Определить при каких объемах производства
данных товаров прибыль будет максимальной;
найти ее максимальное значение.
Например,
![]() =8
(у.е.),
=8
(у.е.),![]() =10
(у.е.),
=10
(у.е.),![]() =
=![]() (у.е.).
(у.е.).
Решение. Так как
товары производятся в объемах х
и у,
то функция прибыли
![]() будет иметь вид
будет иметь вид![]() =
=![]() или
или![]() =
=![]() .
Требуется найти значения переменныхх
и у,
при которых эта функция примет максимальное
значение, при условии, что
.
Требуется найти значения переменныхх
и у,
при которых эта функция примет максимальное
значение, при условии, что
![]() .
Т.е. надо найти максимум функции двух
переменных
.
Т.е. надо найти максимум функции двух
переменных![]() .
.
Для этого найдем
точки возможного экстремума этой
функции, т.е. точки в которых
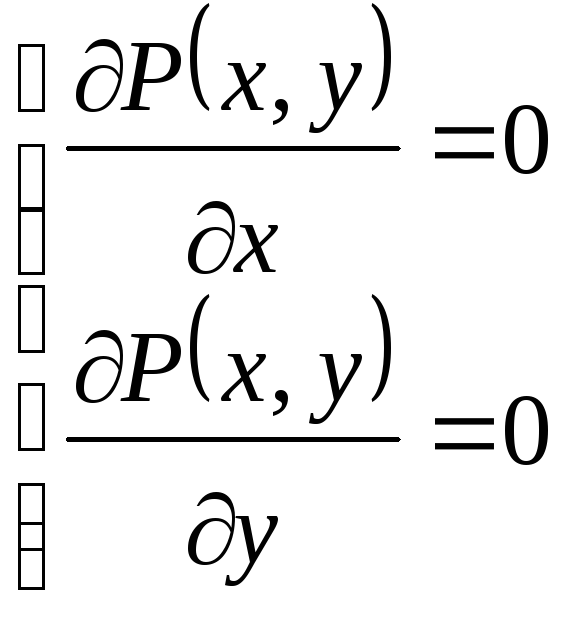 .
В нашей задаче
.
В нашей задаче![]() ;
;![]() ,поэтому система
имеет вид:
,поэтому система
имеет вид: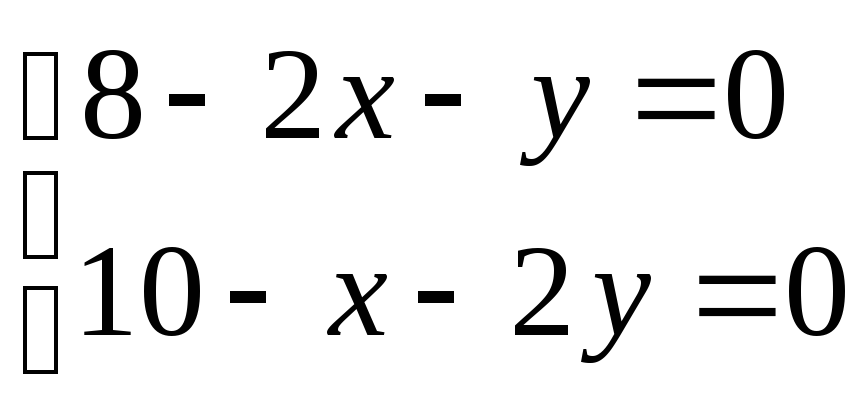 .
Решая ее, находим
.
Решая ее, находим![]() ,
т.е. точка
,
т.е. точка![]() является точкой возможного экстремума.
Если в точке
является точкой возможного экстремума.
Если в точке![]() определитель
определитель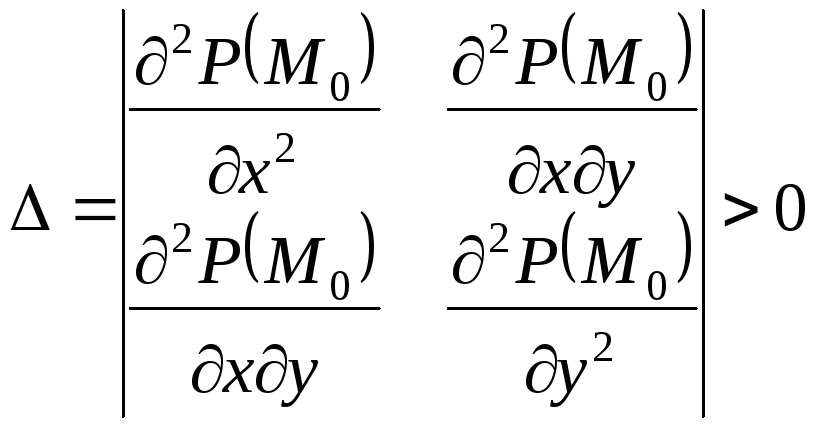 и
и![]() <
0, то точка
<
0, то точка![]() является точкой локального максимума
функции
является точкой локального максимума
функции![]() .
Здесь
.
Здесь![]() ,
,![]() ,
,![]() значения
частных производных второго порядка
функции
значения
частных производных второго порядка
функции![]() в точке
в точке![]() .
.
Вычислим эти
частные производные:
![]() =
=![]() ;
;![]() =
=![]() ;
;![]() .
Тогда
.
Тогда![]() и
и![]() =
=![]() ,
значит точка
,
значит точка![]() является точкой экстремума функции
прибыли
является точкой экстремума функции
прибыли![]() .
Это означает, что, если объемы производства
товаров первого и второго видов будут
равны 2 и 4, соответственно, то прибыль
будет максимальной и ее значение будет
равно
.
Это означает, что, если объемы производства
товаров первого и второго видов будут
равны 2 и 4, соответственно, то прибыль
будет максимальной и ее значение будет
равно![]() (у.е.).
(у.е.).
Решения заданий типа 91-100.
Теоретический справочник
Нахождение
неопределенного интеграла от функции
![]() – это определение множества функций
– это определение множества функций![]() ,
где
,
где![]() – первообразная, т.е.
– первообразная, т.е.![]()
![]() ;с
– произвольная постоянная.
;с
– произвольная постоянная.
Таким образом,
![]() .
.
При интегрировании используют свойства неопределенных интегралов и таблицу.
Свойства неопределенного интеграла
10.
![]()
20.
![]()
30.
![]()
40.
![]() .
.
Таблица основных интегралов
Пусть
![]() дифференцируемая функция.
дифференцируемая функция.
10.
![]()
11.
![]()
12.
![]() .
.
Решения заданий типа 91-100.
Пример 1. Найти
неопределенный интеграл
![]() .
Результат проверить дифференцированием.
.
Результат проверить дифференцированием.
Решение.
![]() =
= =
=![]() .
.
Найдем каждый интеграл отдельно.
![]() =
= =
=
=![]()
![]() =
=![]() =
= =
=![]()
 =
=![]() .
.
Найдем второй интеграл.
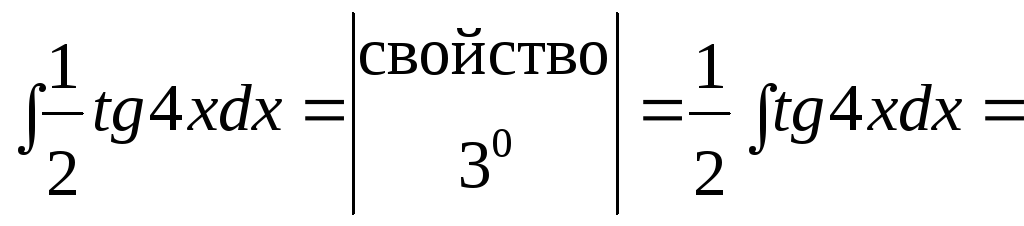
 =
=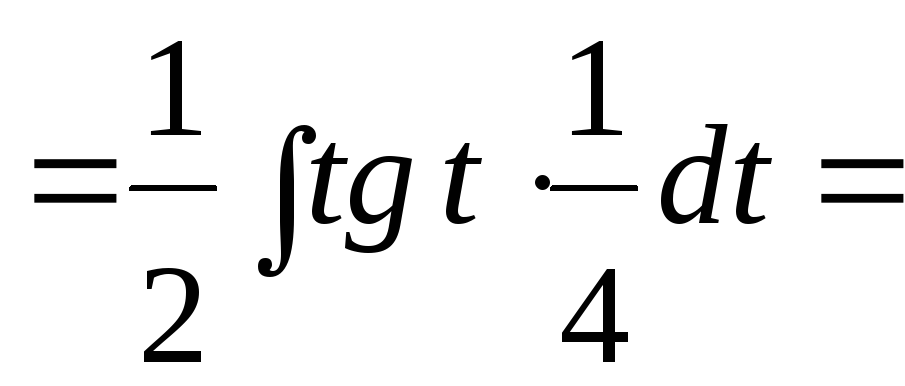
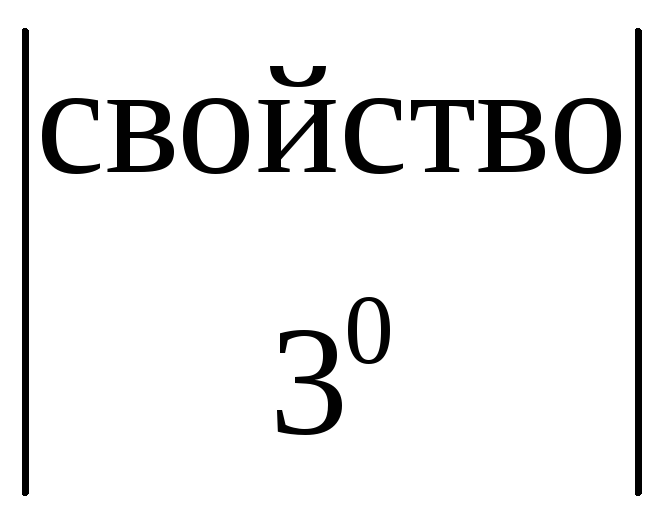 =
=![]()
 =
=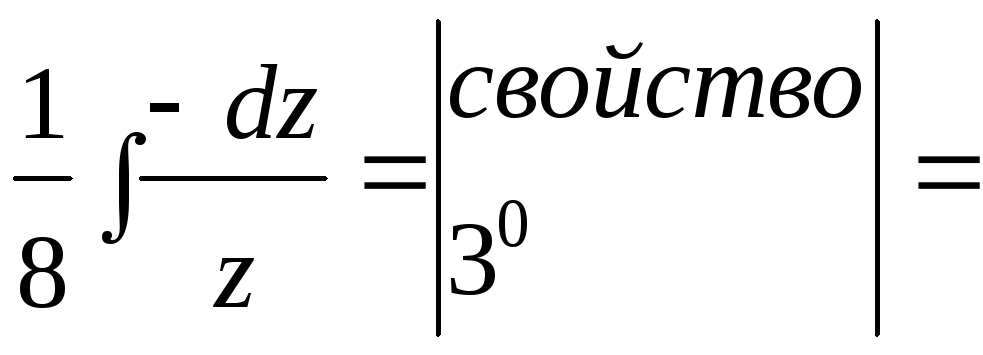
![]()
=
![]()
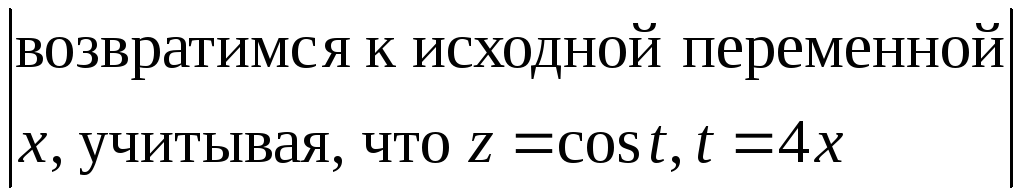 =
=
=![]() .
.
Итак,
![]()
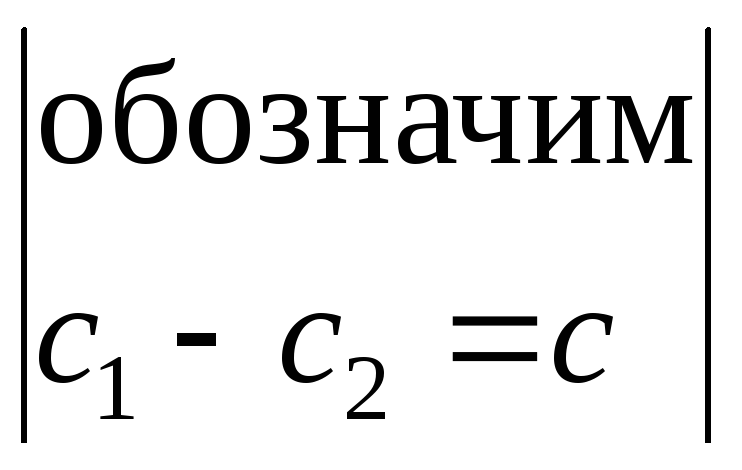 =
=
=![]() .
.
Проверка результата дифференцированием:
![]()
![]() .
Верно.
.
Верно.
Пример 2. Найти
неопределенный интеграл
![]() .
Результат проверить дифференцированием.
.
Результат проверить дифференцированием.
Решение.
![]() =
=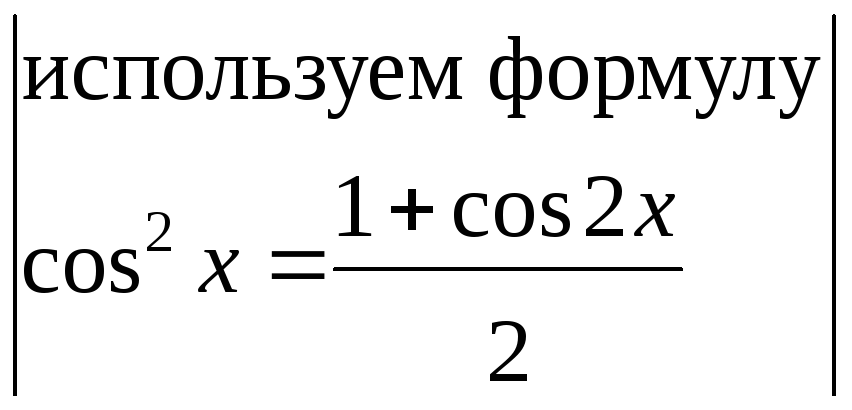 =
=![]() =
=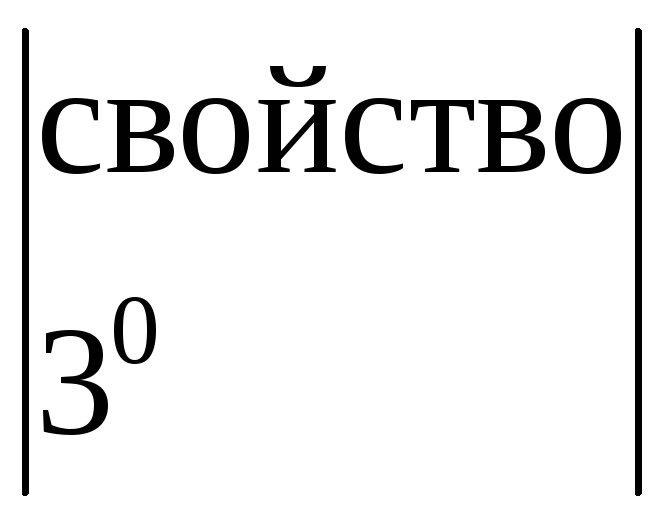 =
=
=![]() =
=![]() =
=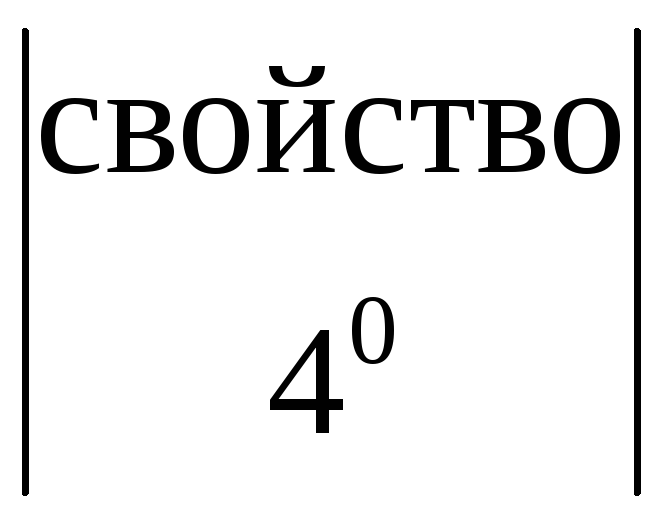 =
=![]() =
=
= =
=![]() .
.
Найдем
![]() с помощью формулы интегрирования по
частям:
с помощью формулы интегрирования по
частям:
![]() ,
,
где функции
![]() и
и![]() выберем таким образом, чтобы интеграл
выберем таким образом, чтобы интеграл![]() получился табличный.
получился табличный.
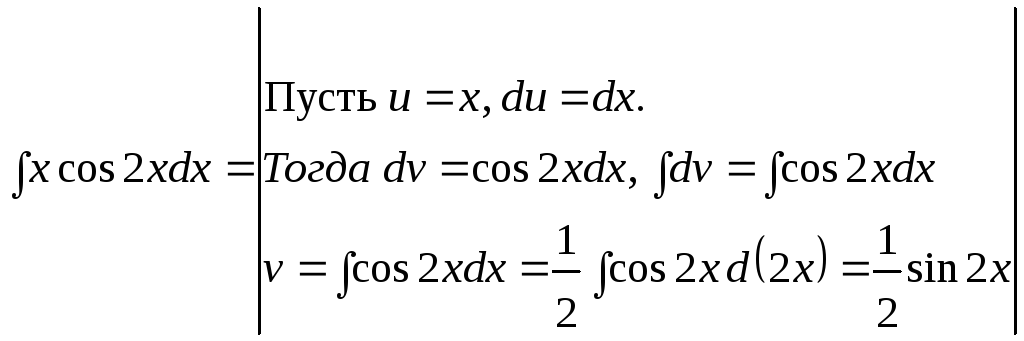 =
=![]() =
=
=![]() =
= =
=![]() .
.
Окончательно,
![]() =
=![]() .
.
Проверка результата дифференцированием:
![]() =
=![]() =
=
=![]() =
=![]() .
Верно.
.
Верно.
Пример 3. Найти
интеграл
![]() .
.
Решение.
![]() =
= =
=![]()
Подынтегральная
функция
![]() является правильной дробью, т.к. степень
числителя строго меньше степени
знаменателя. Разложим знаменатель на
простейшие множители, решив кубическое
уравнение
является правильной дробью, т.к. степень
числителя строго меньше степени
знаменателя. Разложим знаменатель на
простейшие множители, решив кубическое
уравнение![]() .
Подстановкой убеждаемся, чтох
= 1 – корень данного уравнения. Разделим
многочлен
.
Подстановкой убеждаемся, чтох
= 1 – корень данного уравнения. Разделим
многочлен
![]() нах
– 1:
нах
– 1:
![]() .
.
Решая квадратное
уравнение
![]() ,
находим его корни
,
находим его корни![]() и
и![]() Тогда
Тогда![]() ,
а
,
а![]() =
=![]()
![]() .
.
Запишем подынтегральную функцию в виде суммы простейших дробей с неизвестными коэффициентами А, В, С:
![]() =
=![]()
Правую часть приведем к общему знаменателю и сравним числители обеих частей:
![]() .
.
Придавая переменной х произвольные значения, получим значения коэффициентов А, В, С:
при
![]()
при
![]()
при
![]() .
.
Таким образом, исходная подынтегральная дробь разложится на сумму:
![]() =
=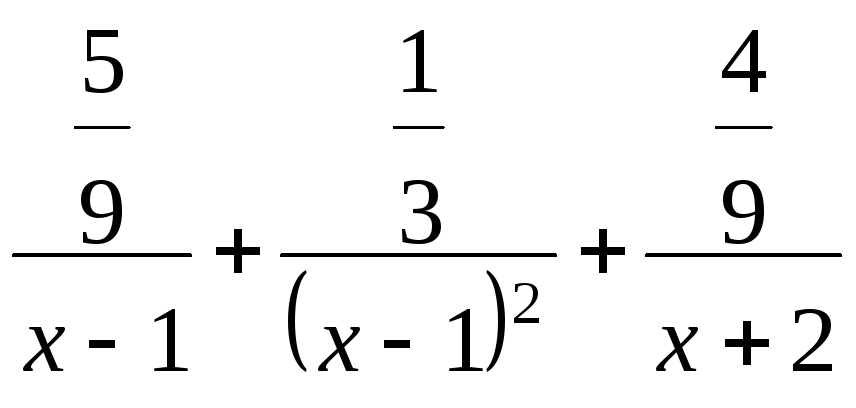 .
.
Возвратимся к интегралу:
![]() =
=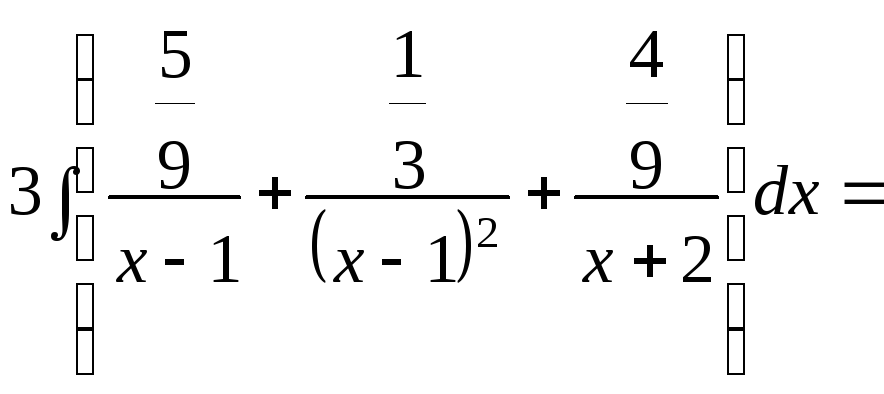
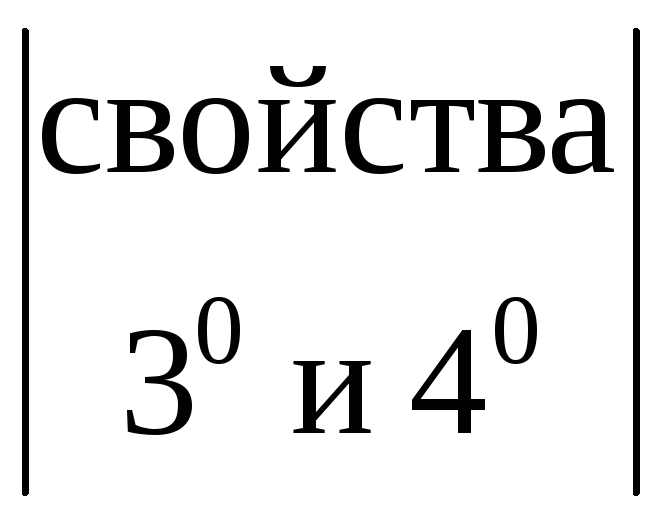 =
=
=![]() =
=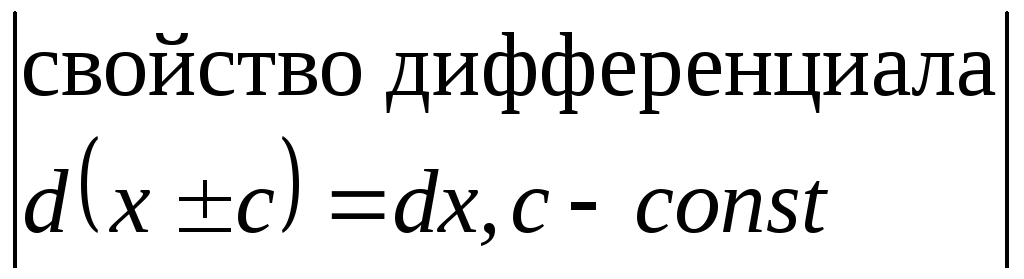 =
=
=![]() =
= =
=
=![]() .
.
Пример 4. Найти
интеграл
![]() .
.
Решение. Подынтегральная функция является правильной дробью. Разложим ее знаменатель на простейшие множители, используя формулу разности квадратов:
![]() .
.
Тогда подынтегральная функция разложится на сумму простейших дробей с неизвестными коэффициентами А, В, С, D:
![]() .
.
Правую часть приведем к общему знаменателю и приравняем числители:
![]()
Придавая переменной х произвольные значения, получим значения коэффициентов А, В, С, D:
при
![]()
при
![]()
при
![]()
при
![]() .
.
Итак, получим разложение
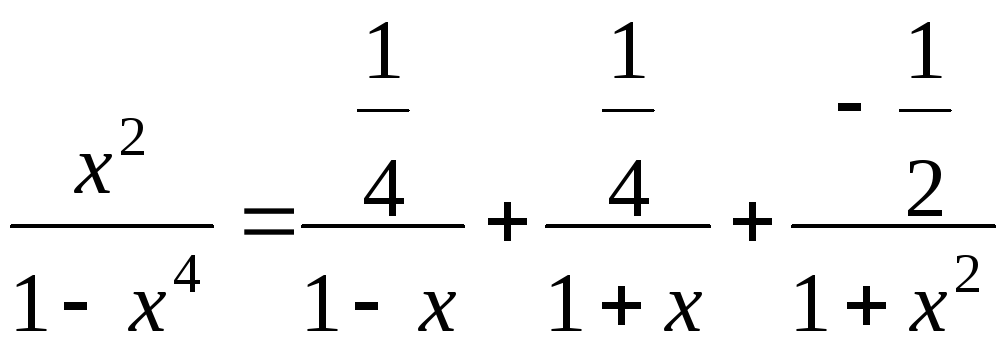 .
.
Тогда интеграл примет вид
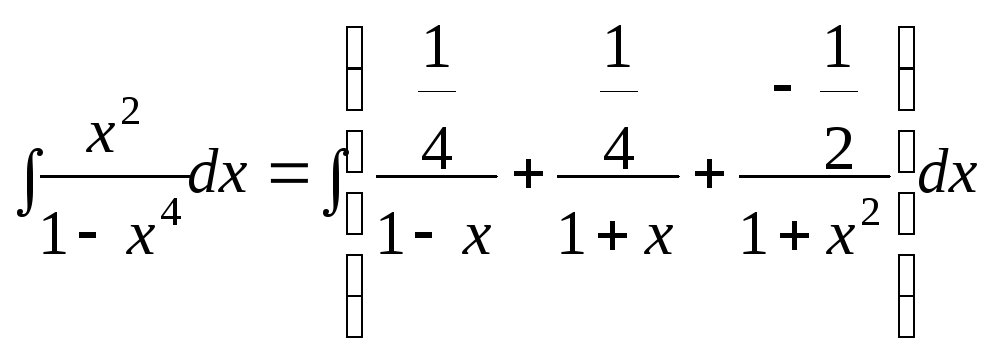 =
=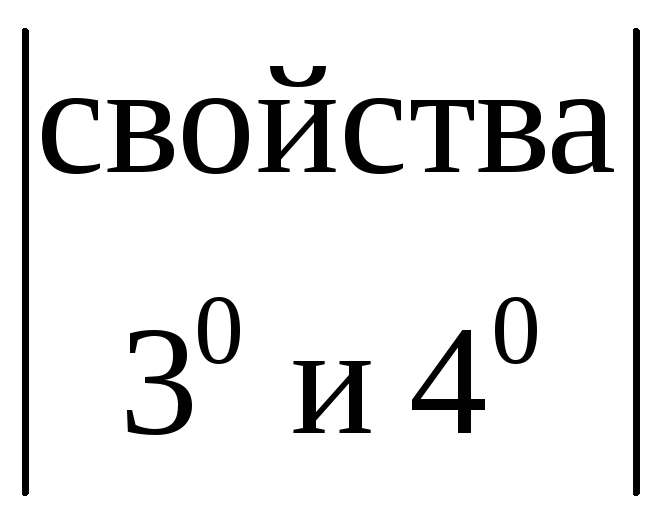 =
=
=![]() =
=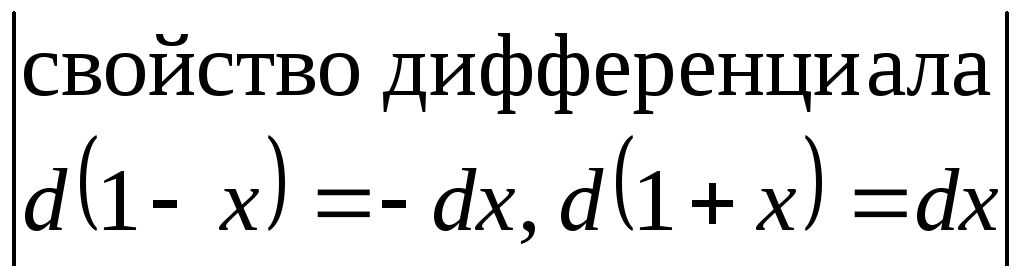 =
=
=![]() =
= =
=
=![]() .
.
Пример 5. Найти
интеграл
![]() .
.
Интегралы от иррациональных функций находятся с помощью подстановок, позволяющих избавиться от иррациональности.
![]() =
=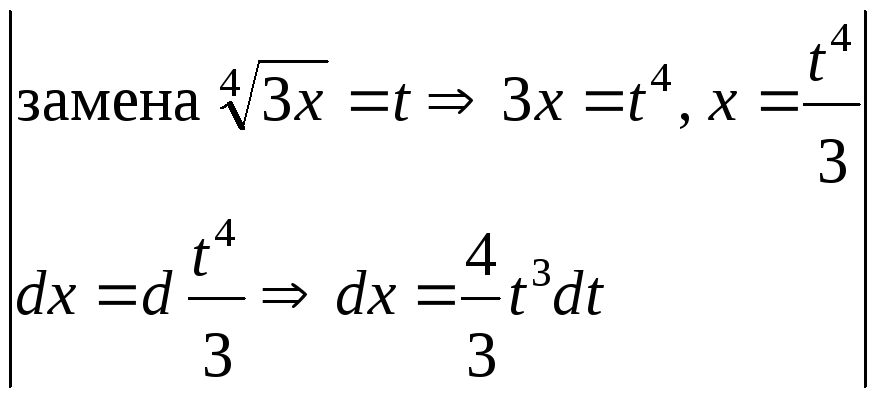 =
= =
=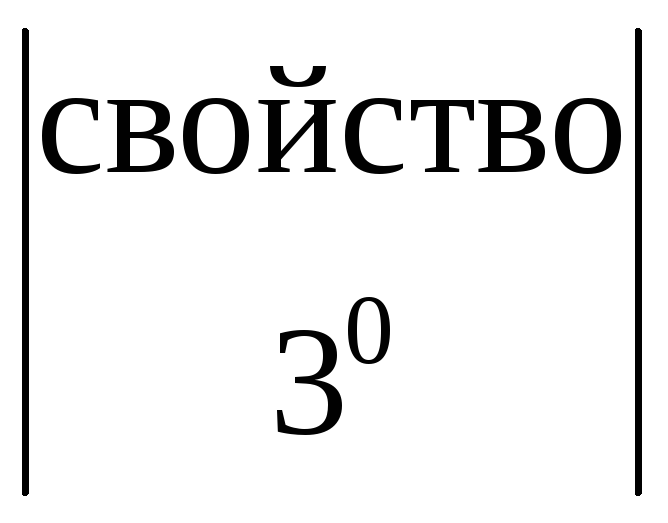 =
=
=![]() =
=![]() =
=![]() =
=
![]() =
=
=![]() =
=![]() =
=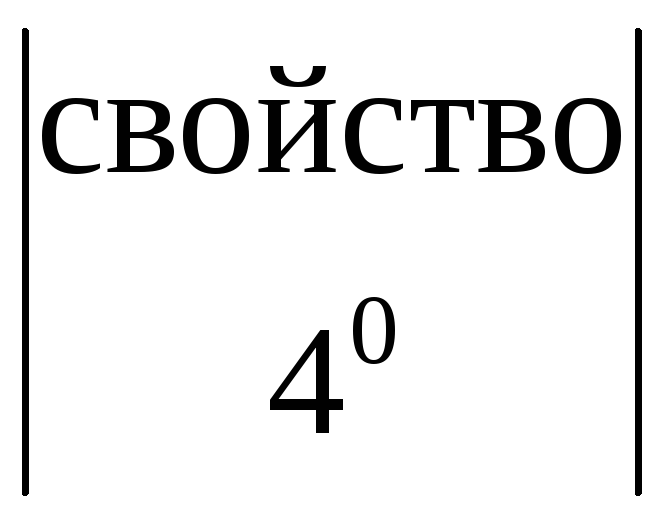 =
=![]()
= =
=![]() =
=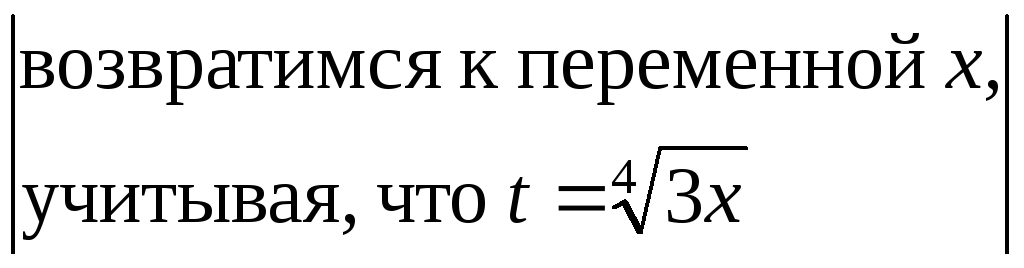 =
=
=![]() .
.
Пример 6. Найти
интеграл
![]() .
.
Если подынтегральная
функция является дробно-рациональной
от функций
![]() и
и![]() ,
то применяют подстановку
,
то применяют подстановку![]() ,
откуда
,
откуда![]() =
=![]() ,
,![]() =
=![]() ,
,![]() .
.
![]() =
=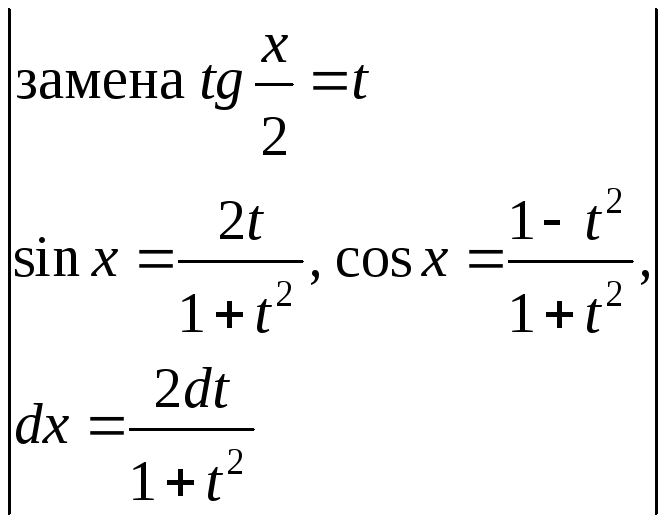 =
=![]()
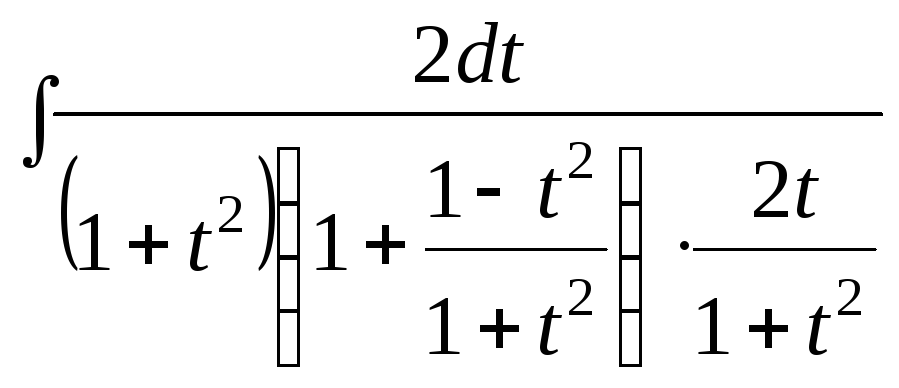 =
=
= =
=![]() =
= =
=![]()
=![]()
 =
=![]() =
= =
=![]() =
=
= =
=![]() .
.
Пример 7. Найти
интеграл
![]() .
.
Выделим у функции в нечетной степени в качестве множителя первую степень и внесем полученную функцию под знак дифференциала.
![]() =
=![]() =
=![]() =
=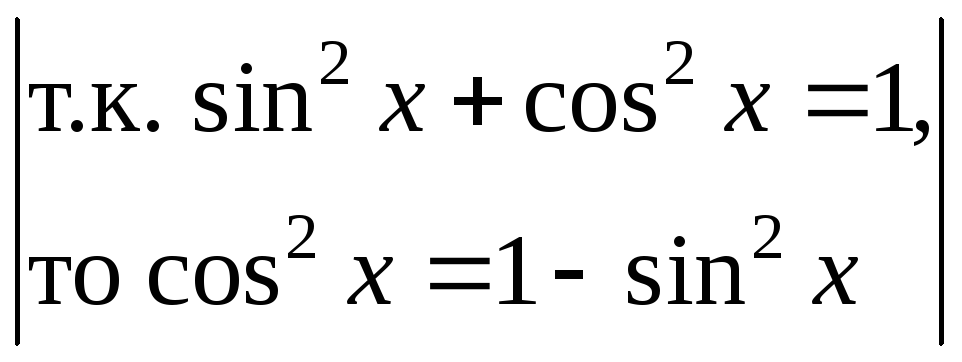 =
=![]() =
=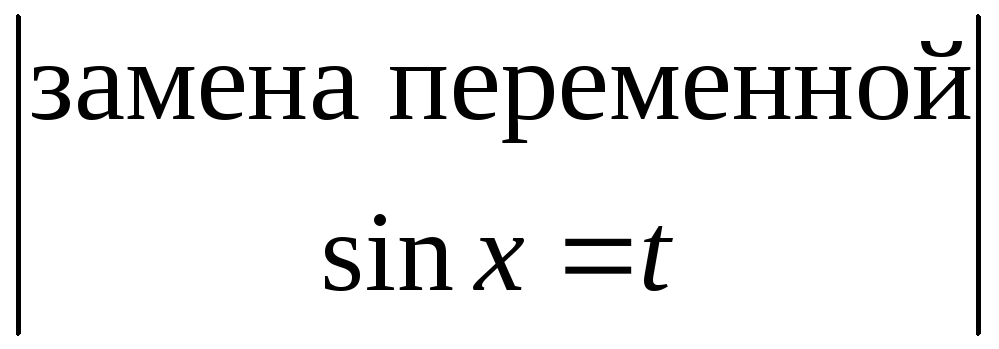 =
=
=![]()
![]()
![]() =
= =
=![]()
=![]() .
.
Решение заданий типа 101-110.
Теоретический справочник
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() и
и![]() - какая-либо первообразная этой функции,
то для вычисления определенного интеграла
- какая-либо первообразная этой функции,
то для вычисления определенного интеграла![]() справедлива формула Ньютона-Лейбница:
справедлива формула Ньютона-Лейбница:
![]() =
=![]()
![]() =
=![]() -
-![]() (1)
(1)
Определенный интеграл используется для вычисления площадей плоских фигур, объемов тел, в приложениях физики и техники, при моделировании экономических процессов.
Объем
![]() произведенной продукции за промежуток
времени ота
до b
при производительности труда
произведенной продукции за промежуток
времени ота
до b
при производительности труда
![]() вычисляется по формуле
вычисляется по формуле
![]() =
=![]() (2)
(2)
Потребительский
излишек
![]() при покупке данного товара – превышение
общей стоимости, которую потребитель
готов уплатить за все единицы товара,
над его реальными расходами на их
приобретение, вычисляется по формуле
при покупке данного товара – превышение
общей стоимости, которую потребитель
готов уплатить за все единицы товара,
над его реальными расходами на их
приобретение, вычисляется по формуле
![]() =
=![]() , (3)
, (3)
где Q
– количество товара, Р
– цена единицы товара,
![]() функция
спроса,
функция
спроса,![]() точка равновесия (состояние рыночного
равновесия характеризуют такие цены и
количество, при которых объем спроса
совпадает с величиной предложения).
точка равновесия (состояние рыночного
равновесия характеризуют такие цены и
количество, при которых объем спроса
совпадает с величиной предложения).
Решение задания типа 101-105.
Сменная
производительность труда рабочего
описывается функцией
![]() ,
,
![]() =
=![]() ,
,
где t
– время в часах,
![]() .
Определить объем выпуска продукции в
течение 22-х
рабочих
дней бригадой, состоящей из 10 человек.
.
Определить объем выпуска продукции в
течение 22-х
рабочих
дней бригадой, состоящей из 10 человек.
Решение. Воспользуемся формулой (2). Тогда количество продукции q, произведенной одним рабочим за 7 часов, равно
![]() =
=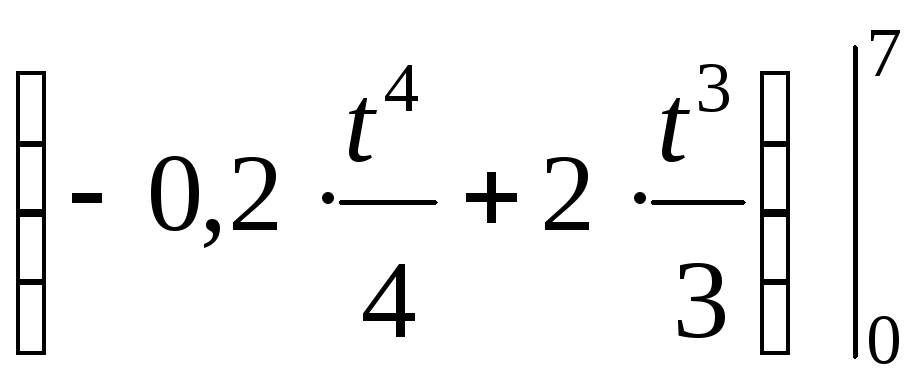 =
=
=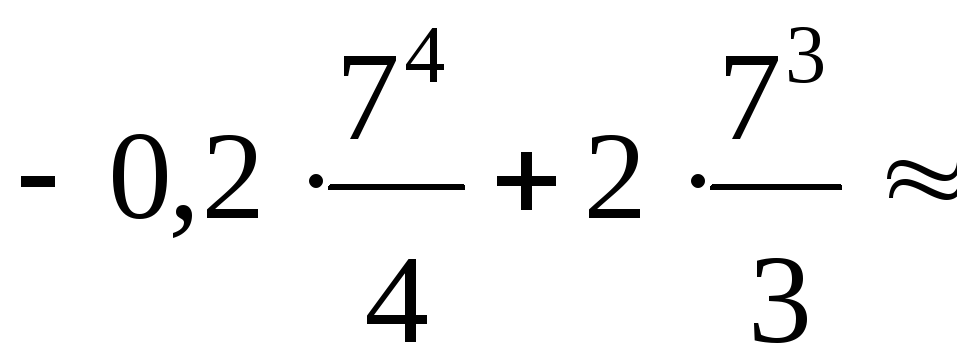 108,6
(усл.ед.)
108,6
(усл.ед.)
Объем продукции, выпущенной в течении 22-х рабочих дней бригадой из 10 человек, составит
![]() (усл.ед.)
(усл.ед.)
Ответ: 23892 (у.е.)
Решение задания типа 106-110.
Известно, что спрос
на некоторый товар описывается функцией
![]() ,
а предложение данного товара характеризуется
функцией
,
а предложение данного товара характеризуется
функцией![]() .
Найти величину излишка потребителя при
покупке данного товара.
.
Найти величину излишка потребителя при
покупке данного товара.
Решение. Для расчета
излишка потребителя сначала определим
параметры рыночного равновесия
![]() .
Для этого решим систему уравнений
.
Для этого решим систему уравнений
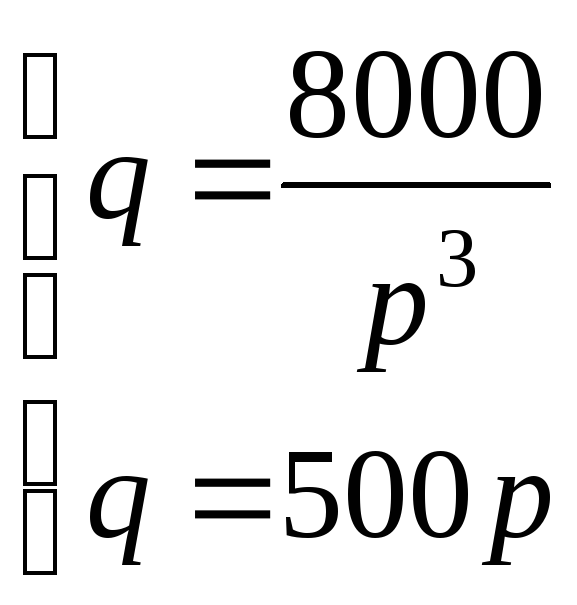
Разделим второе уравнение на первое
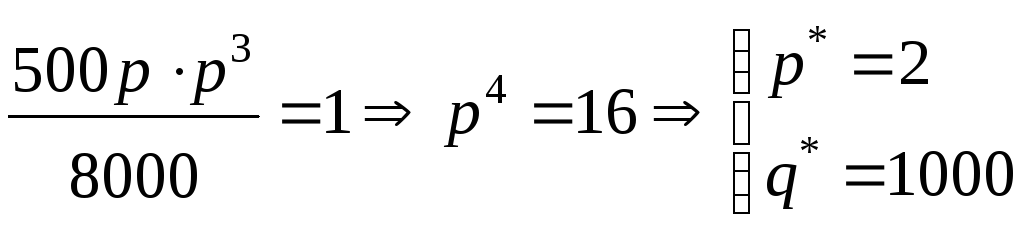 .
.
Запишем формулу
для вычисления потребительского излишка
(3), где
![]() функция,
обратная функции
функция,
обратная функции![]() ,
т.е.
,
т.е.
![]() .
.
Тогда
![]()
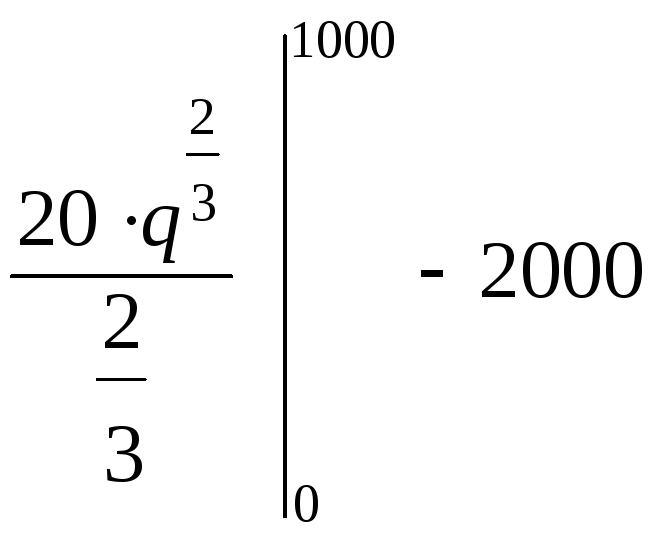 =
=![]() =
=
=![]() .
.
Ответ 1000 (у.е.)
Решение заданий типа 111-120.
Теоретический справочник.
Дифференциальным
уравнением I-го
порядка называется уравнение, связывающее
независимую переменную х,
искомую функцию
![]() и ее производную
и ее производную![]() ,
т.е. уравнение вида
,
т.е. уравнение вида
![]() или
или
![]() .
.
Общим решением
дифференциального уравнения называется
такая функция
![]() ,
,![]() ,
определенная и непрерывно дифференцируемая
в интервале
,
определенная и непрерывно дифференцируемая
в интервале![]() ,
которая обращает данное уравнение в
тождество, т.е.
,
которая обращает данное уравнение в
тождество, т.е.
![]() .
.
Частным решением
дифференциального уравнения называется
решение, получаемое из общего при
конкретном значении произвольной
постоянной с,
которую можно определить из условия
![]() ,
называемое начальным условием.
,
называемое начальным условием.
Чтобы решить дифференциальное уравнение I-го порядка, нужно определить его вид, найти его общее решение, а затем частное решение.
Пример 1. Найти частное решение дифференциального уравнения I порядка
![]() ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию
![]() .
.
Решение. Преобразуем
исходное уравнение, разделив обе его
части на
![]() :
:
![]() или
или
![]() .
Затем разделим обе части уравнения на
.
Затем разделим обе части уравнения на![]() :
:![]() .
Разделив правую часть уравнения (и
числитель, и знаменатель) на
.
Разделив правую часть уравнения (и
числитель, и знаменатель) на![]() ,
получим
,
получим однородное дифференциальное уравнениеI
порядка, т.к. оно имеет вид
однородное дифференциальное уравнениеI
порядка, т.к. оно имеет вид
![]() .
Сделаем замену переменной:
.
Сделаем замену переменной:![]() .
Тогда исходное уравнение примет вид
.
Тогда исходное уравнение примет вид![]() или
или![]() или
или![]() .
Пользуясь свойством пропорции, соберем
возле дифференциалов соответствующие
переменные:
.
Пользуясь свойством пропорции, соберем
возле дифференциалов соответствующие
переменные:![]() и проинтегрируем полученное равенство:
и проинтегрируем полученное равенство:![]() .
Найдем интеграл, стоящий слева:
.
Найдем интеграл, стоящий слева: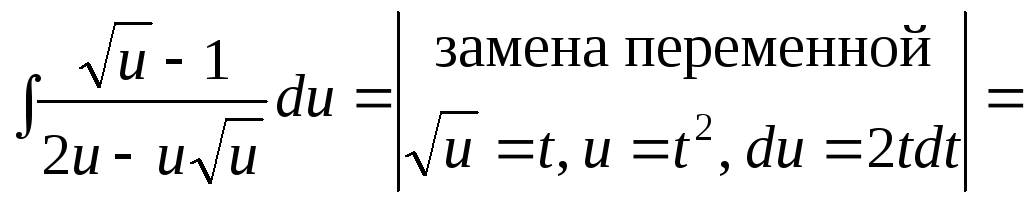
![]() =
=![]() =
=
=![]() =
=![]()
![]() =
=![]() .
.
Найдем интеграл,
стоящий справа:
![]() .
Следовательно,
.
Следовательно,![]() ,
или, возвращаясь к прежним переменным
и обозначая
,
или, возвращаясь к прежним переменным
и обозначая![]() ,
получим
,
получим![]() .
Преобразуем последнее равенство,
используя свойство логарифма
.
Преобразуем последнее равенство,
используя свойство логарифма![]() ,
и получим общее решение
,
и получим общее решение![]() .
Подставив в последнее соотношение
начальное условие
.
Подставив в последнее соотношение
начальное условие![]() ,
найдем конкретное значение произвольной
постоянной:
,
найдем конкретное значение произвольной
постоянной:![]() или
или![]() .
Тогда частное решение примет вид
.
Тогда частное решение примет вид![]() или
или![]() .
.
Ответ:
![]()
Пример 2. Найти
частное решение дифференциального
уравнения I
порядка
![]() ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию![]() .
.
Решение. Разделим
обе части уравнения на
![]() :
:
![]() или
или
![]() .
.
Данное уравнение
является линейным, т.к. имеет вид
![]()
и решается заменой
![]() ,
где
,
где![]() неизвестные
функции;
неизвестные
функции;
![]() .
.
Подставляя выражения
для
![]() в исходное уравнение, получим
в исходное уравнение, получим
![]() .
Сгруппируем слагаемые, содержащие
функцию
.
Сгруппируем слагаемые, содержащие
функцию
![]() :
:![]() .
В качестве функции
.
В качестве функции![]() выбирают одну из функций, удовлетворяющих
уравнению
выбирают одну из функций, удовлетворяющих
уравнению![]() или
или![]() .
Интегрируем последнее соотношение,
разделяя переменные:
.
Интегрируем последнее соотношение,
разделяя переменные:![]() или
или![]() ,
,![]() ,
,![]() ,
,![]() .
Тогда функция
.
Тогда функция![]() определится из уравнения
определится из уравнения![]() .
Подставляя найденную функцию
.
Подставляя найденную функцию![]() ,
получим
,
получим![]() или
или![]() или
или![]() .
Интегрируя последнее уравнение, найдем
функцию
.
Интегрируя последнее уравнение, найдем
функцию![]() :
:![]() .
Итак, общее решение имеет вид
.
Итак, общее решение имеет вид![]() или
или![]() .
Подставляя начальные данные
.
Подставляя начальные данные![]() ,
получаем уравнение:
,
получаем уравнение:![]() откуда
откуда![]() .
Частное решение имеет вид
.
Частное решение имеет вид![]() .
.
Решение заданий типа 121-130.
Теоретический справочник.
Линейным неоднородным
дифференциальным уравнением II-го
порядка с постоянными коэффициентами
называется уравнение вида:
![]() ,
гдеp
и q
– некоторые числа,
,
гдеp
и q
– некоторые числа,
![]() – заданная функция. Общее решение
данного уравнения представляет собой
сумму общего решения
– заданная функция. Общее решение
данного уравнения представляет собой
сумму общего решения![]() соответствующего однородного уравнения
соответствующего однородного уравнения![]() и частного решения
и частного решения![]() данного неоднородного уравнения.
данного неоднородного уравнения.
Пример 1. Найти
общее решение дифференциального
уравнения II-го
порядка
![]() .
.
Решение. Общее
решение исходного уравнения имеет вид
![]() .
Запишем соответствующее однородное
уравнение
.
Запишем соответствующее однородное
уравнение![]() и
составим для него характеристическое
уравнение: для этого заменим
и
составим для него характеристическое
уравнение: для этого заменим![]() на
на![]() ;
;![]() на
на![]() ,у
на
,у
на
![]() .
Получим квадратное уравнение
.
Получим квадратное уравнение![]() с корнями
с корнями![]()
Т.к. корни
характеристического уравнения
действительные и различные, то общее
решение
![]() однородного уравнения будет
однородного уравнения будет![]() или для нашего примера
или для нашего примера![]() ,
где
,
где![]() и
и![]() – произвольные постоянные.
– произвольные постоянные.
Частное решение
неоднородного уравнения
![]() будем искать в том же виде, какова правая
часть, но с неопределенными коэффициентами,
и с учетом кратности корней
характеристического уравнения, а именно,
будем искать в том же виде, какова правая
часть, но с неопределенными коэффициентами,
и с учетом кратности корней
характеристического уравнения, а именно,![]() .
В нашем случае
.
В нашем случае![]() является однократным корнем
характеристического уравнения, поэтому
является однократным корнем
характеристического уравнения, поэтому![]() .
Таким образом,
.
Таким образом,![]() .
.
Определим неизвестные
коэффициенты А
и В.
Для этого найдем
![]() и
и![]() :
:
![]() =
=![]() =
=![]() .
.
![]() =
=![]()
![]() ,
и подставим значения
,
и подставим значения![]() ,
,![]() и
и![]() в исходное уравнение:
в исходное уравнение:![]() =
=
=
=![]() .
Сократим обе части равенства на
.
Сократим обе части равенства на![]() и приведем подобные слагаемые:
и приведем подобные слагаемые:![]() .
Сравним коэффициенты при одинаковых
степеняхх:
.
Сравним коэффициенты при одинаковых
степеняхх:
при х : 12А = 12
при
![]() .
.
Получим систему уравнений для нахождения неизвестных коэффициентов А и В:
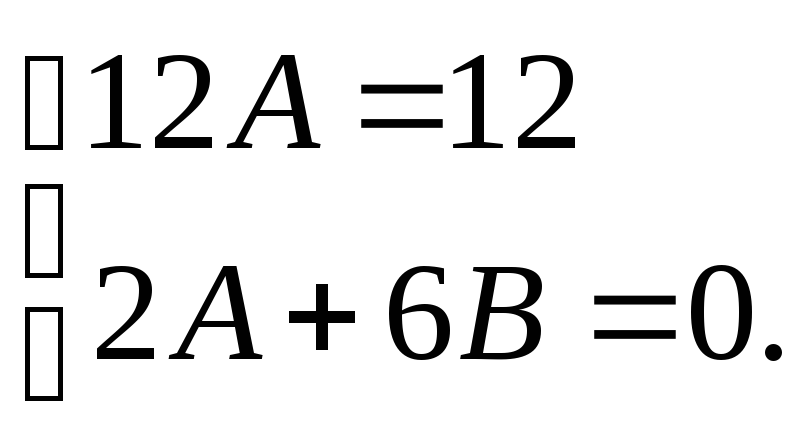 Откуда
Откуда
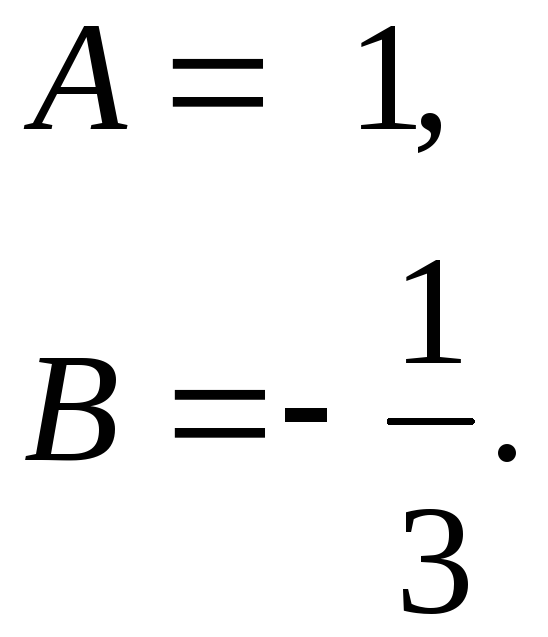
Итак,
![]() или
или![]() Окончательно, общее решение уравнения
имеет вид
Окончательно, общее решение уравнения
имеет вид![]() .
.
Пример 2. Найти
общее решение дифференциального
уравнения II-го
порядка
![]() .
.
Решение. Общее
решение исходного уравнения имеет вид
![]() .
Запишем соответствующее однородное
уравнение
.
Запишем соответствующее однородное
уравнение![]() .
Составим характеристическое уравнение
.
Составим характеристическое уравнение![]() .
Его корни
.
Его корни![]() .
Т.к. корни характеристического уравнения
действительные и кратные, то общее
решение
.
Т.к. корни характеристического уравнения
действительные и кратные, то общее
решение![]() однородного уравнения будет
однородного уравнения будет![]() или в нашем случае
или в нашем случае
![]() ,
где
,
где
![]() и
и![]() произвольные
постоянные.
произвольные
постоянные.
Частное решение
![]() будем искать в том же виде, какова правая
часть
будем искать в том же виде, какова правая
часть![]() ,
но с неопределенными коэффициентами
,
но с неопределенными коэффициентами![]() :
:![]() .
.
Найдем
![]() и
и![]() :
:
![]() =
=![]() =
=
=
=![]() .
.
![]() =
=![]() =
=
=![]() .
.
Подставим
![]() ,
,![]() и
и![]() в исходное уравнение и, приведя подобные
слагаемые, получим:
в исходное уравнение и, приведя подобные
слагаемые, получим:
![]() .
.
Сравним коэффициенты
при
![]() и
и![]() :
:
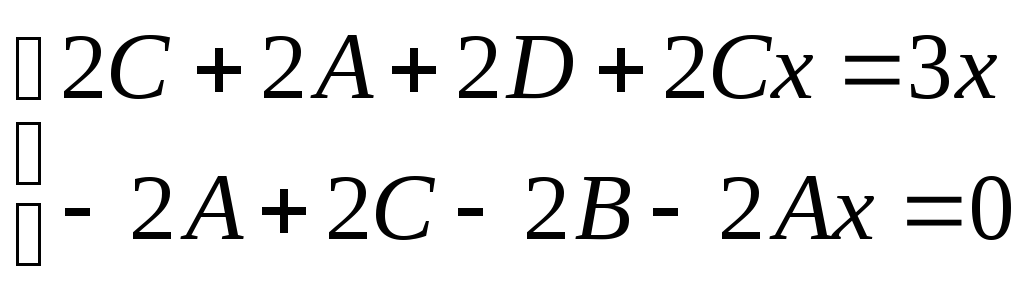 .
.
Сравним коэффициенты при одинаковых степенях переменной х; получим систему
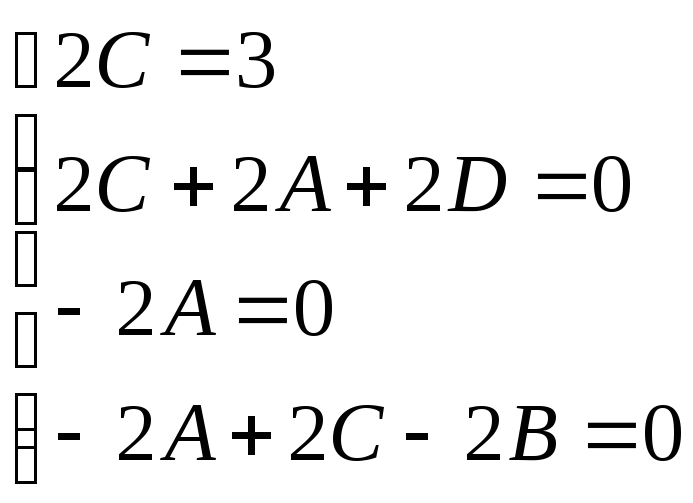 .
.
Следовательно,
![]() .
.
Тогда
![]() =
=![]() .
.
Окончательно, общее решение уравнения примет вид
![]() .
.
Методические указания для выполнения контрольной работы № 3.
Решение заданий типа 131-140.
Пример 1. Исследовать
на сходимость числовой ряд
![]() .
.
Решение. Данный
числовой ряд является знакоположительным
рядом, следовательно, для его исследования
на сходимость можно применить радикальный
признак Коши. Согласно этому признаку,
если для ряда
![]() ,
то ряд
,
то ряд![]() сходится, если же
сходится, если же![]() ,
то ряд
,
то ряд![]() расходится. В нашем примере
расходится. В нашем примере![]() =
=![]() .
Применяя радикальный признак Коши,
вычислим
.
Применяя радикальный признак Коши,
вычислим![]()
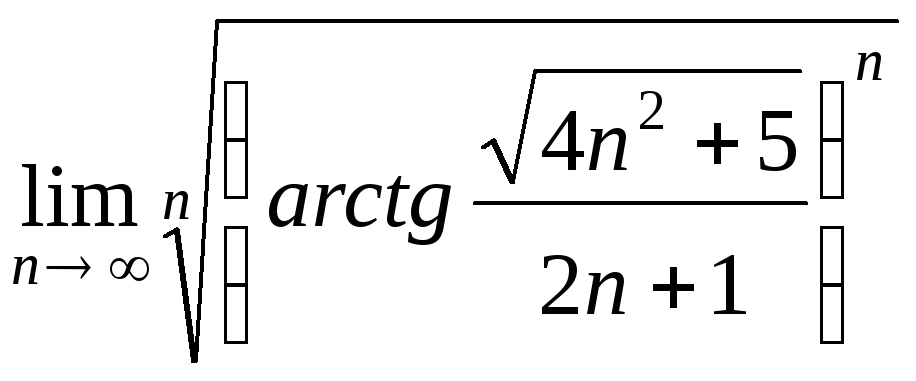 =
=
=![]() =
= =
=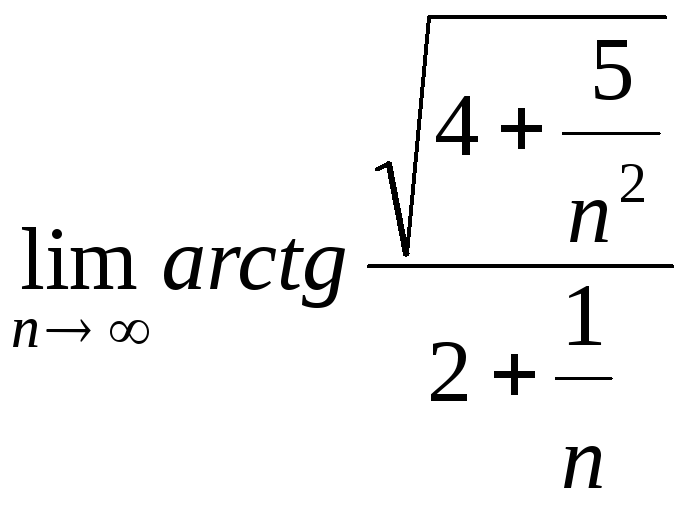 =
=
=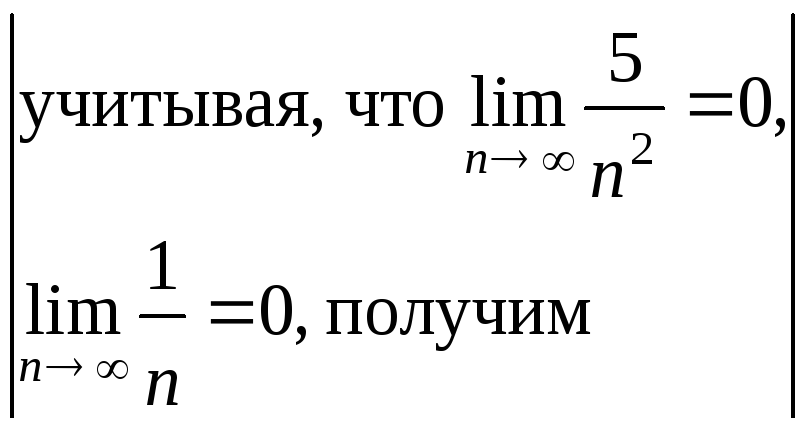 ==
==![]() .
Очевидно, что
.
Очевидно, что![]() ,
следовательно, данный ряд является
сходящимся.
,
следовательно, данный ряд является
сходящимся.
Пример 2. Исследовать
на сходимость числовой ряд
![]() .
.
Решение. Данный
числовой ряд является знакоположительным
рядом, поэтому для его исследования на
сходимость можно применить признак
Даламбера. По признаку Даламбера, если
для ряда
![]() ,
то ряд
,
то ряд![]() сходится, если же
сходится, если же![]() ,
то ряд
,
то ряд![]() расходится. Здесь
расходится. Здесь![]() - член ряда с номером
- член ряда с номером![]() получается из формулы
получается из формулы![]() ,
заменой
,
заменой![]() на
на![]() .
.
В нашем примере:
![]() ,
тогда
,
тогда![]() =
=
=
=![]() .
.
Вычислим
![]() =
=![]()
![]() =
=![]() =
=
=![]() =
=![]()
![]() =
=
=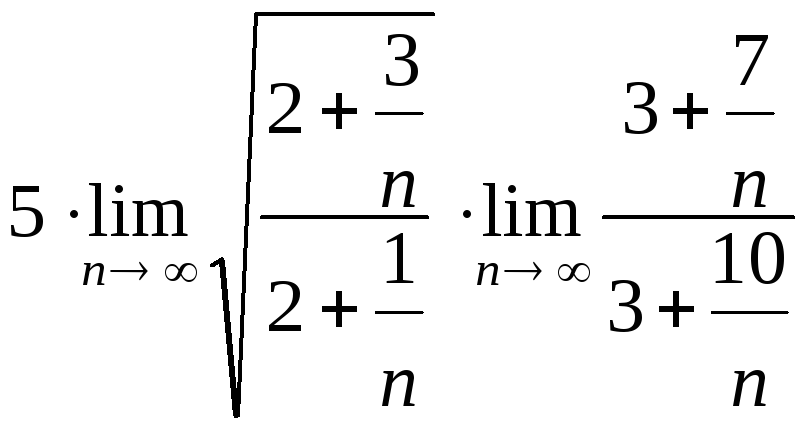 =
= =5.
Очевидно, что 5>1, значит данный ряд
является расходящимся.
=5.
Очевидно, что 5>1, значит данный ряд
является расходящимся.
Решение заданий типа 141-150.
Найти область
сходимости степенного ряда
![]() .
.
Решение. Данный
ряд является обобщенным степенным рядом
вида
![]() ,
где коэффициент
,
где коэффициент![]() ,
,![]() .
.
Областью сходимости
степенного ряда
![]() с точностью до границ, является интервал
с центром в точке
с точностью до границ, является интервал
с центром в точке![]() и радиусом
и радиусом![]() ,
гдеR
– радиус сходимости степенного ряда
определяется по формуле
,
гдеR
– радиус сходимости степенного ряда
определяется по формуле
![]() .
Сходимость ряда
.
Сходимость ряда![]() на концах интервала при
на концах интервала при![]() и
и![]() необходимо исследовать отдельно. В
нашем примере
необходимо исследовать отдельно. В
нашем примере
![]() ,
тогда
,
тогда
![]() .
.
Вычислим радиус
сходимости
![]() =
=![]()
=![]() =
=![]() =
=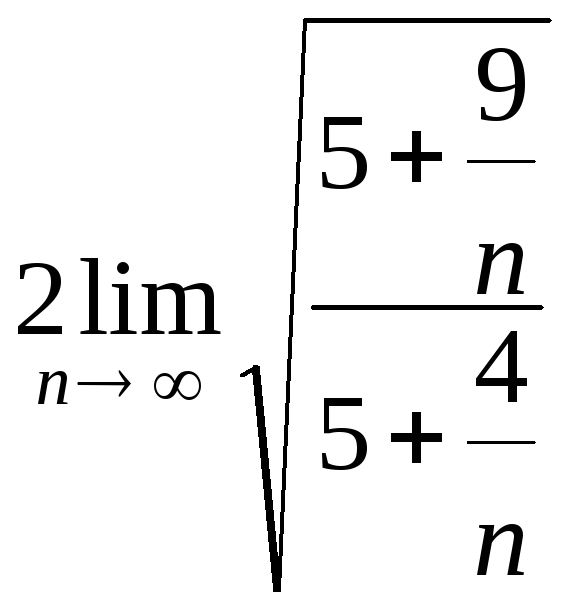 =
=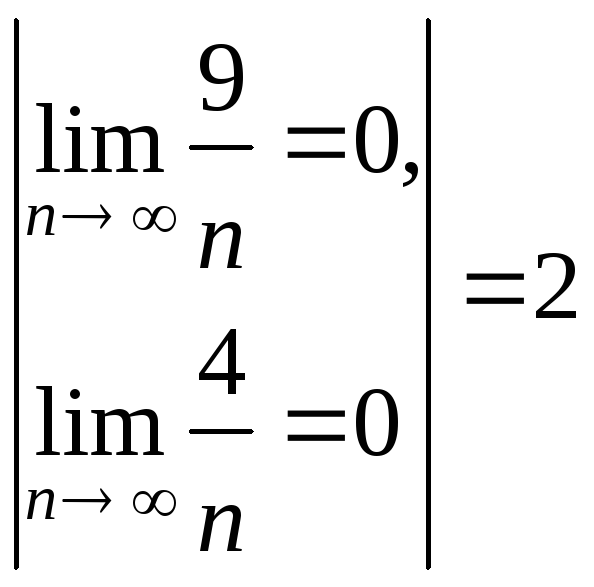 .
.
Тогда интервал
сходимости имеет вид
![]() или
или![]() .
.
Исследуем сходимость
степенного ряда на концах интервала.
Пусть
![]() ,
тогда подставив это значение в степенной
ряд, получим числовой ряд
,
тогда подставив это значение в степенной
ряд, получим числовой ряд![]() или, преобразовав его, имеем ряд
или, преобразовав его, имеем ряд![]() .
Мы получили числовой знакочередующийся
ряд, который исследуется признаком
Лейбница.
.
Мы получили числовой знакочередующийся
ряд, который исследуется признаком
Лейбница.
Согласно признаку
Лейбница, если в знакочередующемся ряде
выполняются два условия: 1) члены ряда
с возрастанием номера
![]() ,
убывают по абсолютной величине; 2) предел
абсолютной величины общего члена ряда
равен нулю при
,
убывают по абсолютной величине; 2) предел
абсолютной величины общего члена ряда
равен нулю при![]() ,
то такой ряд является сходящимся.
,
то такой ряд является сходящимся.
Проверим выполнимость условий Лейбница в нашем примере:
1)![]() ,
,![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() ,
…
,
…
Очевидно, что члены ряда по абсолютной величине убывают:
![]() >
>
![]() >
>![]() >
>![]() >
…>
>
…>![]() >
>![]() >
…
>
…
2)
![]() .
.
Оба условия признака
Лейбница выполняется, следовательно,
при
![]() степенной ряд
степенной ряд![]() сходится.
сходится.
Пусть
![]() ,
тогда данный степенной ряд станет
числовым знакоположительным рядом
,
тогда данный степенной ряд станет
числовым знакоположительным рядом![]() =.
=.![]() .
.
К исследованию
этого ряда на сходимость применим
признак сравнения с рядом Дирихле
![]() ,
который сходится, если
,
который сходится, если![]() и расходится если
и расходится если![]() .
.
Для нашего примера
используем ряд
![]() =
=![]() ,
здесь
,
здесь![]() ,
значит, данный ряд расходится.
,
значит, данный ряд расходится.
Сравнение выполним
посредством вычисления предела
![]() =
=![]() =
=![]() =
=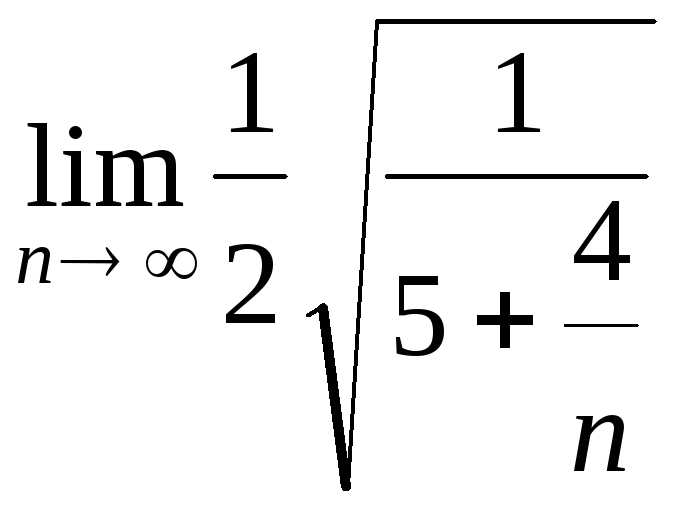 =
=![]() =
=![]() ,
так как предел получился отличным от 0
и
,
так как предел получился отличным от 0
и![]() ,
значит, исследуемый ряд
,
значит, исследуемый ряд![]() ведет себя также, как и тот ряд, с которым
проводилось сравнение
ведет себя также, как и тот ряд, с которым
проводилось сравнение![]() ,
т.е. в нашем случае
,
т.е. в нашем случае![]() расходится, а это означает, что при
расходится, а это означает, что при![]() степенной ряд
степенной ряд![]() расходится. Итак, область сходимости
данного степенного ряда:
расходится. Итак, область сходимости
данного степенного ряда:![]() .
.
Решение задания типа 151-160.
Производится залп из трех орудий. Вероятность попадания в цель первым орудием равна 0,9, вторым – 0,85, третьим – 0,95. Какова вероятность 1) хотя бы одного попадания в цель; 2) ровно двух попаданий.
Решение. Обозначим
события
![]() .
Из условия задачи вероятности этих
событий равны
.
Из условия задачи вероятности этих
событий равны![]() .
Соответственно, вероятности противоположных
событий равны
.
Соответственно, вероятности противоположных
событий равны![]() ;
;![]() ;
;![]() .
.
1) Требуется найти
вероятность события
![]() .
Противоположное событие
.
Противоположное событие![]() .
.
Так как события
![]() независимы, то применима теорема
умножения вероятностей:
независимы, то применима теорема
умножения вероятностей:![]() .
.
Известно, что
![]() .
Отсюда
.
Отсюда![]() .
.
2). Событие
![]() в алгебре событий с помощью событий
в алгебре событий с помощью событий![]() можно записать как
можно записать как![]() .
Так как события
.
Так как события![]() и
и![]() независимы и несовместны, то по теоремам
сложения и умножения вероятностей
получим
независимы и несовместны, то по теоремам
сложения и умножения вероятностей
получим![]()
=![]() =
=
![]() .
.
Решение задания типа 161-170.
В продажу поступило 40% телевизоров с первого завода, 50% - со второго, 10% - с третьего. Вероятность того, что телевизор, изготовленный на первом заводе, имеет дефект, равна 0,1. Для телевизоров, изготовленных на втором и третьем заводах, эти вероятности соответственно равны 0,15 и 0,2. 1) Какова вероятность приобрести исправный телевизор? 2) Приобретен исправный телевизор. Найти вероятность того, что он поступил с первого завода.
Решение.
1). Пусть событие
![]() .
Это событие может произойти с одной из
следующих гипотез:
.
Это событие может произойти с одной из
следующих гипотез:![]() ,
,![]() ,
,
![]() .
.
Из условия задачи вероятности гипотез равны:
![]() ;
;
![]() ;
;![]() .
.
При этом должно
выполняться равенство
![]() ,
что действительно так: 0,4+0,5+0,1=1.
,
что действительно так: 0,4+0,5+0,1=1.
Вычислим условные вероятности
 .
.
Аналогично
![]() и
и![]() .
.
Вероятность того,
что наудачу купленный телевизор без
дефекта, по формуле полной вероятности
равна
![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=
=![]() .
.
2) Пересчитаем
вероятность гипотезы
![]() ,
если известно, что событие
,
если известно, что событие![]() произошло, т.е. найдем условную вероятность
произошло, т.е. найдем условную вероятность![]() .
.
По формуле Байеса
![]() =
=![]() .
.
Решения заданий типа 171-180.
Непрерывная СВ Х
задана функцией распределения
![]() =
=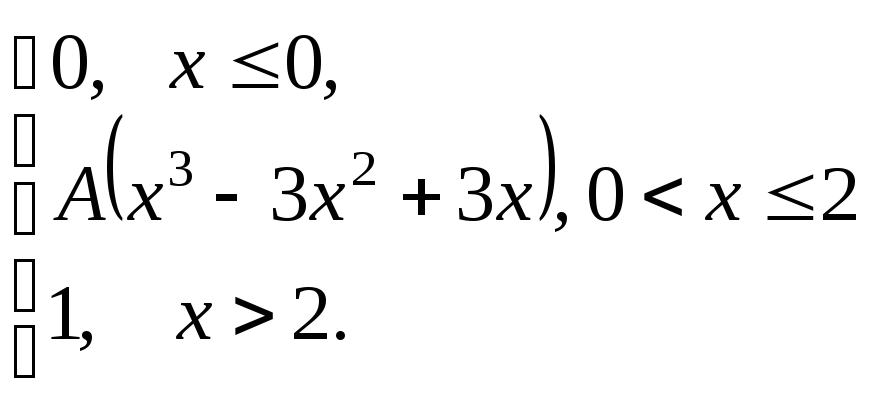
Найти:
коэффициент А;
плотность распределения вероятностей
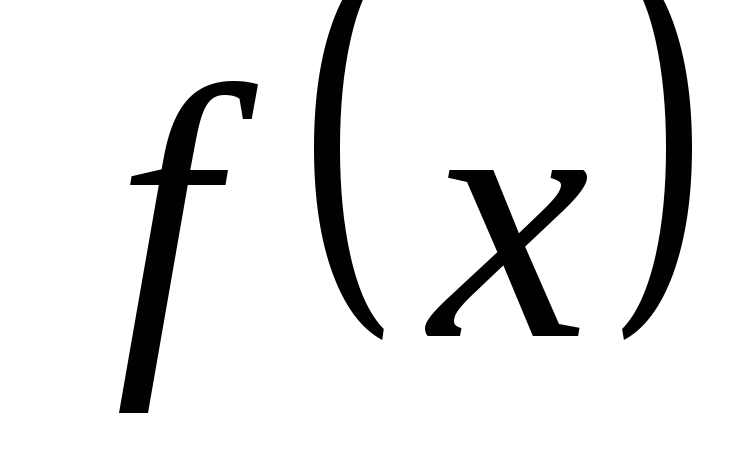 ;
;математическое ожидание СВ Х;
вероятность события
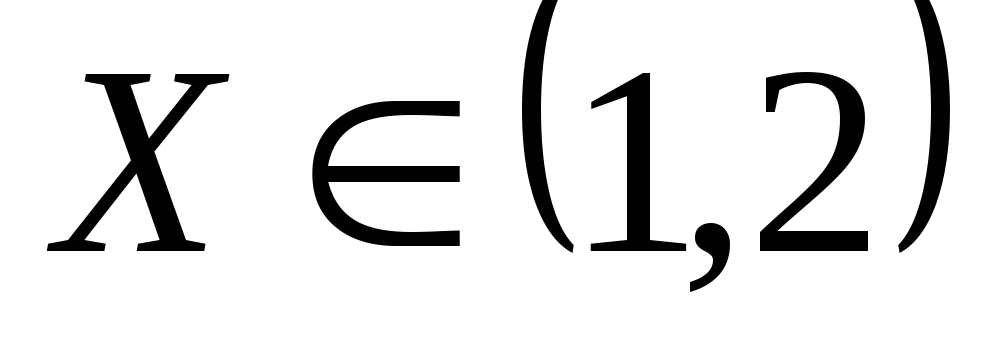 .
.
Решение. 1). Из
непрерывности функции распределения
![]() и свойства
и свойства![]() следует, что
следует, что![]() .
Откуда
.
Откуда![]() .
.
2). Плотность
распределения вероятностей
![]() найдем из формулы
найдем из формулы![]() =
=![]() :
:
![]() =
=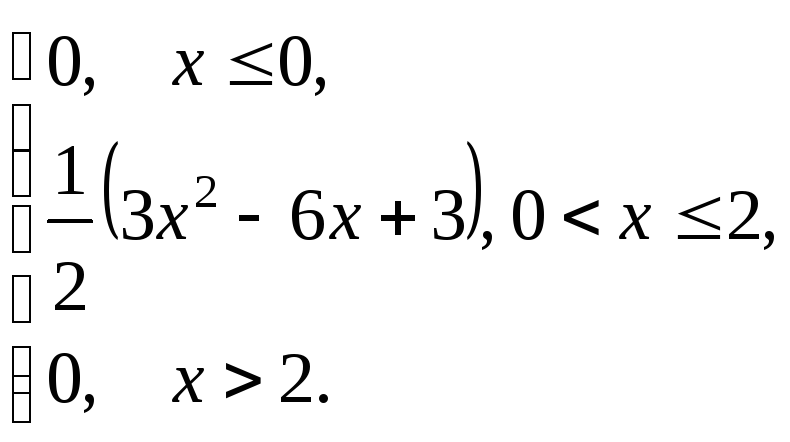
3). Математическое
ожидание
![]() непрерывной СВ определяется формулой
непрерывной СВ определяется формулой![]() =
=![]() .
Так как функция
.
Так как функция![]() задана тремя различными выражениями
на трех интервалах, то несобственный
интеграл разобьется на сумму трех
интегралов:
задана тремя различными выражениями
на трех интервалах, то несобственный
интеграл разобьется на сумму трех
интегралов:
![]() =
=![]() +
+![]() +
+![]() =
=![]() =
=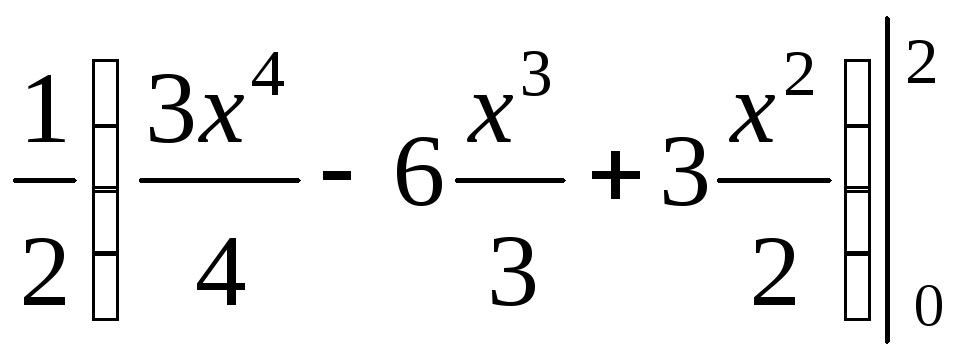 =
=![]() .
.
4). Вероятность
события
![]() найдем по формуле
найдем по формуле![]() .
В нашем случае
.
В нашем случае![]() и поэтому
и поэтому![]() .
.
Задание задания типа 181-190.
Зависимость выпуска валовой продукции (с.в. Y) от стоимости основных фондов (с.в. Х) 50 предприятий представлена корреляционной таблицей
|
X Y |
0,3 |
0,9 |
1,5 |
2,1 |
2,7 |
mi |
|
0,6 |
1 |
|
|
|
|
1 |
|
1,8 |
2 |
5 |
|
|
|
7 |
|
3,0 |
1 |
6 |
8 |
5 |
|
20 |
|
4,2 |
|
|
9 |
8 |
|
17 |
|
5,4 |
|
|
|
2 |
3 |
5 |
|
mj |
4 |
11 |
17 |
15 |
3 |
n = 50 |
В первом столбце таблицы указаны наблюдаемые значения с.в. Х (xi), в последнем столбце – соответствующие частоты наблюдаемых значений (mi). В первой строке таблицы указаны наблюдаемые значения с.в. Y (yj), в последней строке – соответствующие частоты (mj) появление этих значений. На пересечении строк и столбцов таблицы указаны частоты (mij) появления пары (xi,yj).
Требуется:
Найти уравнение прямой линии регрессии Y на Х.
Найти уравнение прямой линии регрессии Х на Y.
Построить графики полученных прямых.
Оценить тесноту корреляционной связи, используя выборочный коэффициент корреляции.
Решение.
1. Эмпирическую линейную функцию регрессии Y на Х ищем в виде
![]()
Используя метод наименьших квадратов, получим расчетные формулы для определения неизвестных параметров а и b, а именно, систему двух уравнений с двумя неизвестными:
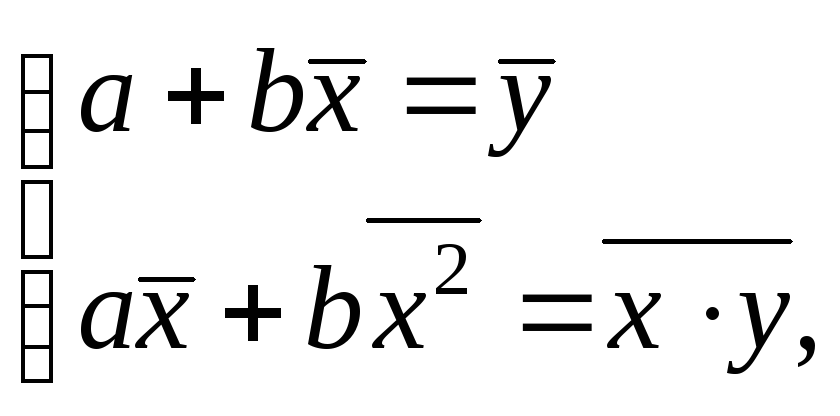
где выборочные
средние
![]() и
и![]() вычисляются по формулам:
вычисляются по формулам:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
В нашем случае
![]()
![]()
![]()
![]()
![]() 5,7528
5,7528
Подставив данные значения в систему уравнений, получим
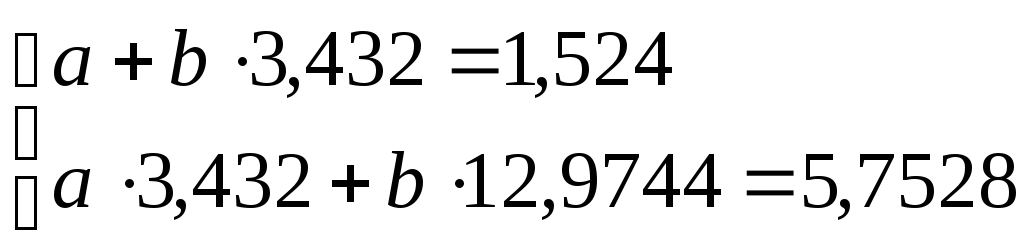
Решая систему,
получим оценки параметров
![]() и
и![]()
Окончательный вид
уравнения регрессии Y
на Х:
![]() .
.
2. Уравнение прямой
линии регрессии Х
на Y
ищем в виде
![]() ,
где числовые параметрыс
и d
найдем из системы
,
где числовые параметрыс
и d
найдем из системы
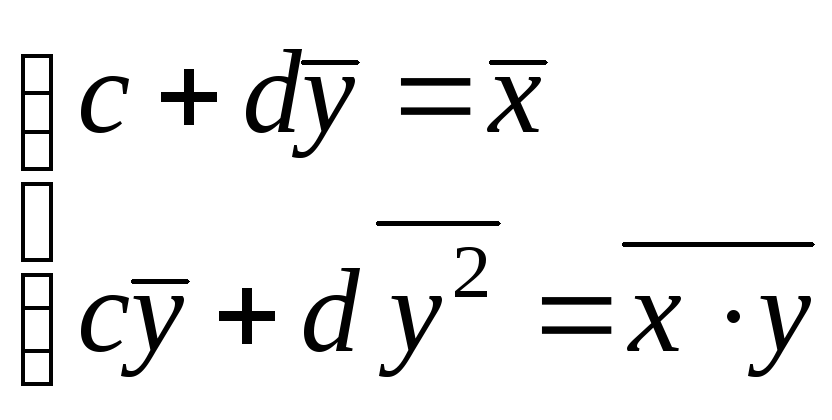 .
.
Выборочное среднее
![]() вычислим по формуле
вычислим по формуле![]() =
=![]() ,
а именно
,
а именно
![]() =
=![]()
Подставив значения
![]() и
и![]() в систему, получим:
в систему, получим:
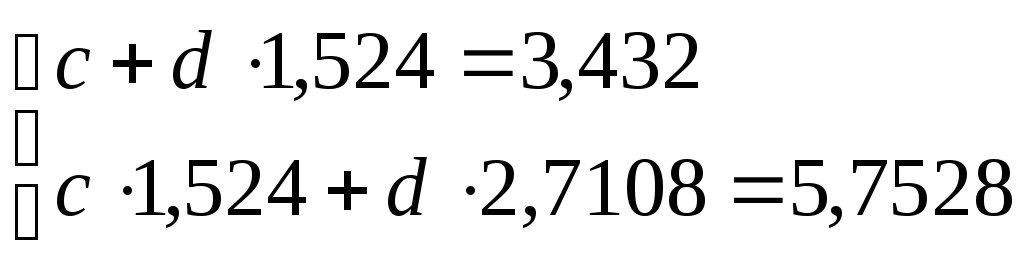
Откуда
![]() и
и![]() .
.
Окончательный вид
уравнения регрессии Х
на Y:
![]() .
.
3. Построим графики найденных прямых регрессий.

4. Определим
выборочный коэффициент корреляции
![]() по формуле
по формуле
![]() ,
,
где выборочные
средние квадратические отклонения
![]() и
и![]() вычисляются по формулам
вычисляются по формулам![]() =
=![]() ,
,![]() =
=![]() .
.
В нашем случае
![]() =
=![]() ,
,![]() =
=![]() .
Тогда
.
Тогда![]() .
.
На практике теснота
корреляционной связи оценивается по
значению коэффициента
![]() следующим образом:
следующим образом:
![]()
![]() пренебрежимо
малая;
пренебрежимо
малая;
![]()
![]()
![]() слабая;
слабая;
![]()
![]()
![]() существенная;
существенная;
![]()
![]()
![]() большая;
большая;
![]()
![]() очень
большая, близкая к функциональной.
очень
большая, близкая к функциональной.
Так как в нашем
случае
![]() =
=![]() ,
то теснота связи между случайными
величинамиХ
и Y
большая.
,
то теснота связи между случайными
величинамиХ
и Y
большая.

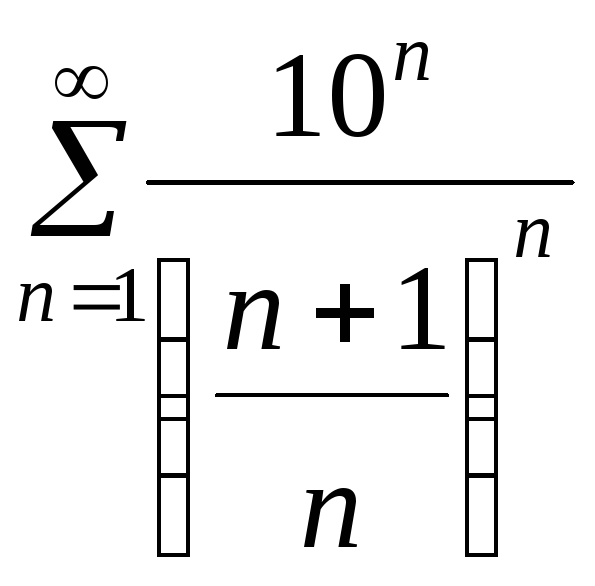 .
.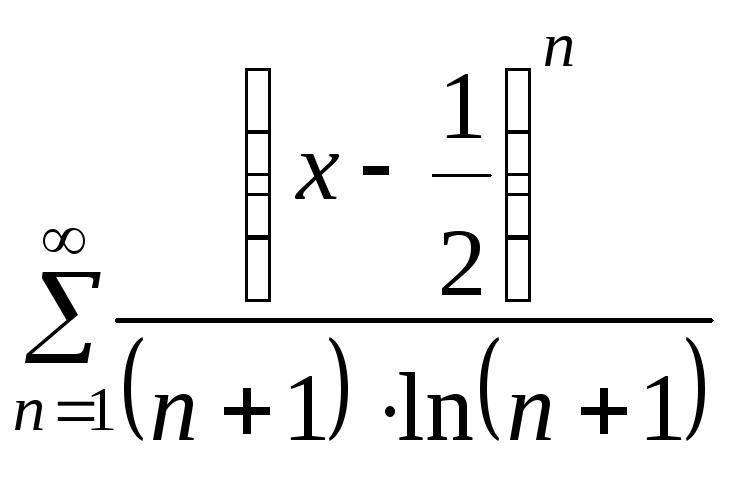 .
.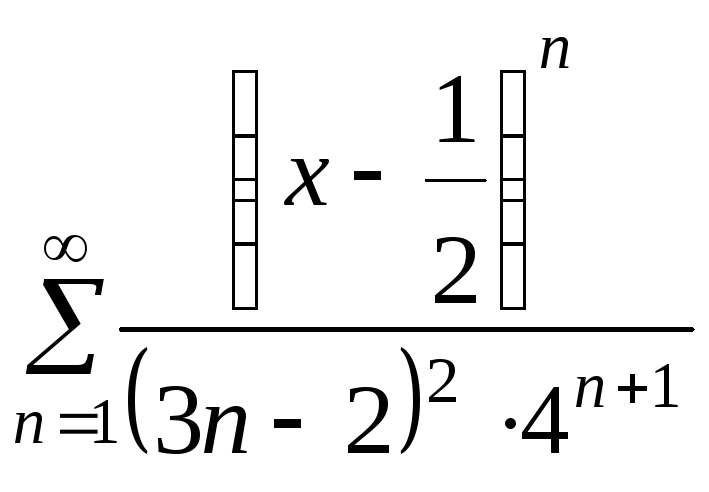 .
.