
Пособие ДМ2
.pdf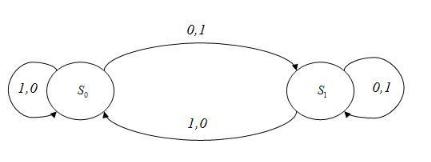
Пример. Рассмотрим автомат с двумя устойчивыми состояниями, изображенный на рисунке
Здесь заданы - входная строка ̅ |
и начальное со- |
|
стояние |
. Отсюда получим: |
|
.
В реальных устройствах увеличение числа внутренних состояний автомата приводит к росту числа электронных схем и следовательно к уменьшению надёжности, к усложнению ремонта и т.д. Поэтому число необходимых состояний автомата стремятся уменьшить, не ограничивая его возможностей. В связи с этим важна следующая задача.
Пусть фиксированы входной и выходной алфавиты.
Можно ли заменить автомат |
|
автоматом с |
|
меньшим числом состояний |
̅ |
̅ |
̅ ̅ , но с той же |
функцией, переводящей входы в выходы. |
|
||
Определение. Автомат |
̅ |
покрывает |
автомат , если |
входной и выходной алфавиты у этих автоматов общие и су-
ществует функция : |
̅ |
такая что для любого положи- |
|
, |
|||
тельного числа r |
|
|
|
̅ |
̅ |
̅ |
̅ |
Указанный факт записывается в виде ̅ |
. |
||
Автомат, который нельзя покрыть меньшим автоматом называется минимальным. Можно проверить, что отношение
покрытия является рефлексивным и транзитивным. |
|
||||||||
|
Автоматы |
и ̅ называются эквивалентными, |
если |
||||||
покрывает ̅ и одновременно с этим ̅ покрывает |
. В этом |
||||||||
случае пишут |
̅. |
|
|
|
|
|
|
||
|
Эквивалентность автоматов означает, что существуют |
||||||||
функции f и g такие, что |
|
|
|
|
|
||||
: |
|
̅ |
|
|
̅ |
̅ |
̅ |
̅ |
|
|
со свойством |
|
|
|
|||||
: |
̅ |
со свойством |
̅ |
̅̅ |
|
̅ ̅ |
̅ |
̅ |
|
|
|
|
̅ . |
||||||
|
Следствие Отношение эквивалентности автоматов сим- |
||||||||
метрично, транзитивно, рефлексивно. |
|
|
|
||||||
|
|
|
2.2.2. Покрытия и морфизмы |
|
|
||||
|
Отношения покрытия и эквивалентности тесно связаны с |
||||||||
понятием морфизма. |
|
|
|
|
|
|
|||
|
Пусть имеются автоматы |
и ̅ с общими входными и |
|||||||
выходными алфавитами. |
|
|
|
|
|
||||
|
Морфизмом называют отображение : |
̅ |
|
||||||
|
, такое, что |
||||||||
̅ |
|
|
|
и ̅ |
|
|
|
|
|
Если θ сюрьективно, то морфизм называется эпиморфизмом. Если θ биективно, то морфизм называется изоморфизмом (автоматом).
Пусть отображение θ - эпиморфизм автомата |
на ̅. То- |
||
гда для любой входной строки |
и началь- |
||
ного состояния |
выходная строка ̅ |
ав- |
|
томата |
совпадает с выходной строкой ̅, если начальное |
||
состояние ̅ удовлетворяет условию ̅̅̅ |
. |
|
|
Таким образом, любой эпиморфизм автоматов : |
̅ |
||
определяет покрытие автомата автоматом ̅. |
|
|
|
Определение. Автоматы |
и |
̅ |
|
̅ |
̅ ̅ , имеющие общие алфавиты и |
изоморфны, |
|
если: 1) |
у них одинаковое число внутренних состояний и |
||
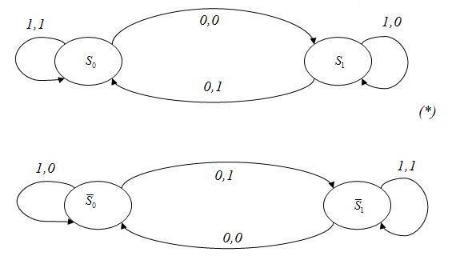
2)существует биекция : ̅такая, что любая входная строка перерабатывается в одну и ту же выходную строку автоматами и ̅ с начальными состояниями и .̅ соответственно.
Например, автоматы, представленные на рисунке
изоморфны, так как имеет место биекция : |
̅и . |
̅ |
2.2.3. Эквивалентные состояния автоматов
Пусть дан автомат . Требуется построить новый автомат ̅, который:
1)покрывает (возможно, даже, эквивалентен ему)
2)имеет наименьшее число состояний среди всех автоматов,
покрывающих . Считается, что функции φ и ψ всюду определены.
Далее следует определить эквивалентные друг другу состояния автомата . Затем следует склеить все эквивалентные состояния в одно.
Определение. Состояния автоматов и называются r- эквивалентными, если для любой входной строки длины r
( ̅ |
) имеет мест |
̅ |
̅ ( |
̅) В эт м случ е ис- |
|
п льзуется з пись |
Если эт |
е т к т |
исп льзуется |
||
з пись |
. Если |
ля любого r, то говорят, что со- |
|||
стояния и эквивалентны и записывают |
. |
||||
Отношения Er и E представляют собой отношения эквивалентности. Классы эквивалентности отношения E1 являются множествами всех пар состояний, перерабатывающих каждый входной символ в фиксированный выходной символ. То
есть запись |
з ч ет чт |
|
|
|
( |
) |
. |
В этом равенстве легко убедиться по таблице состояний. Например, для автомата, заданного таблицей состояний:
Текущее |
|
|
|
φ |
|
|
|
|
|
|
||
состояние |
|
0 |
|
1 |
|
0 |
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
S |
0 |
|
S |
2 |
|
S |
|
|
0 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||
S |
|
|
S |
0 |
|
S |
2 |
|
1 |
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|||
S |
2 |
|
S |
0 |
|
S |
|
|
0 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||
В данном случае имеем |
|
|
|
. Таким образом, отношение |
||||||||
эквивалентности |
состоит |
|
из |
следующих элементов: |
||||||||
Дополнение отношения |
|
обозначается как . Тогда запись |
||||||||||
|
означает, что |
|
|
|
. Таким образом: |
|||||||
Задача минимизации сводится к определению попарно эквивалентных состояний и последующему их склеиванию. При этом, оказывается эффективнее всего выявить в начале неэквивалентные состояния.
Вводятся функции φ* и ψ*

Определение: Функция |
, задаваемая выраже- |
|
нием |
|
|
̅ |
|
|
указывает на то, что |
̅ –есть конечное состояние, |
в |
которое переходит автомат, начав работу из состояния s0 |
и |
|
считав строку ̅ длины r. |
|
|
Определение: Функция |
, задаваемая выра- |
|
жением |
|
|
̅ |
|
|
указывает на то, что ̅ - есть последний символ выходной строки, которую печатает автомат, начав работу из состояния s0 и считав строку ̅ длины r.
Например, для первого автомата, изображенного на рисунке ( ) при имеем:
.
2.3. Процедура минимизации конечных автоматов
Процедура минимизация основана на рассмотрении отношений эквивалентности между упорядоченными парами состояний конечного автомата.
Рассмотрим таблицу состояний автомата.
Текущее |
|
|
|
|
|
|
|
|
состояние |
|
a1 |
a2 |
a3 |
|
a1 |
a2 |
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
0 |
1 |
1 |
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
0 |
1 |
1 |
Рис. 1. Таблица состояний автомата, подлежащего минимизации.
Начнем с нахождения отношений |
и . В соответ- |
||||
ствии с функцией , находим первое разбиение |
|
||||
: |
|
|
|
. |
(1) |
Оно разбивает состояния автомата на два класса эквива- |
|||||
лентности |
и |
(здесь вместо |
пишется 1, вместо |
пи- |
|
шется 2 и т.д.). Так как отношение |
рефлексивно и симмет- |
||||
рично, то его всегда можно восстановить по множеству тех
пар |
, для которых выполняется условие |
, Обо- |
|
значим его через . Обозначим, в общем случае, через |
|||
множество |
упорядоченных пар |
, со свойствами |
|
. Для разбиения имеем: |
|
|
|
={(1,3)(1,5)(1,7)(1,8)(3,5)(3,7)(3,8)(5,7)(5,8)(7,8,)(2,4)(2
,6)(2,9)(4,6)(4,9)(6,9)},
={(1,2)(1,4)(1,6)(1,9)(2,3)(3,4)(3,6)(3,9)(2,5)(4,5)(5,6)(5,
9)(2,7)(4,7)(6,7)(7,9)(2,8)(4,8)(6,8)(8,9)}. |
|
||||
Так как |
и |
– |
классы эквивалентности |
||
относительноE1, имеемs1E1s3, s1E1s5 |
и s1 |
s2, s1 s4и т.д. |
|||
Множество |
состоит из элементов множества и ещё |
||||
пар (2,9), (4,9) и (6,9). Например, a3 |
переводит (2,9) в (4,7), а |
||||
эта последняя парапринадлежит G( |
|
). Добавление этих пар к |
|||
G( ) определяет новое разбиение на классы эквивалентно- |
|||||
сти: |
|
|
|
|
|
: |
|
|
|
|
(2) |
Определим теперь множество |
G |
. Оно состоит из эле- |
|||
3 |
|||||
ментов множества |
G |
|
|
|
|
2 и еще двух пар (2,6) и (4,6). |
|||||
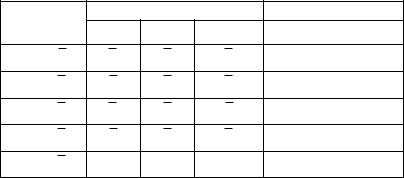
Например,
a |
2 |
|
переводит (2,6) в (4,9), а эта последняя
пара принадлежит |
|
.При разбиении π3имеем следующие |
G2 |
классы эквивалентности:
(3)
Дальнейший перебор показываетπ5 = π4 и E4 = E. Конструкция покрывающего автомата теперь несложна.
Каждый класс эквивалентности последнего разбиения становится состоянием нового автомата. Например, обозначается через ̅ , через ̅ и т.д. Получается автомат с 5-ю состояниями, покрывающий первоначальный автомат с 9-ю состояниями. Так как выходы для каждого начального состояния в фиксированном классе эквивалентности не зависит от этого состояния при односимвольных входах, то в таблице состояний нового автомата выход прямо считывается с таблицы состояний первоначального автомата. Чтобы построить функцию перехода в следующее состояние, выберем по состоянию siв каждом классе , и если элемент a A переводит siв неоторое состояние из , положим φ(si, a) = ̅̅̅̅. Заметим, что это предписание однозначно: все s переходят в состояния из после считывания из a A.
Результат этой процедуры, примененной к автомату с рис. 1, показан на рис. 2. Получен минимальный автомат.
Текущее
состояние
S1
S |
2 |
|
|
S |
3 |
|
|
S |
4 |
|
S5
Следующее состояние
a1 |
a2 |
a3 |
S |
2 |
S |
2 |
S |
3 |
||||||
|
|
|
|
|
|
||||||
S |
|
|
S |
2 |
S |
2 |
|||||
1 |
|
|
|
|
|||||||
S |
4 |
S |
2 |
S |
|
|
|||||
|
|
|
|
1 |
|||||||
S |
|
|
S |
5 |
S |
4 |
|||||
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
S3 |
S5 |
S3 |
|||||||||
Выход
a1 |
a2 |
a3 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
|
|
Рис. 2. Минимальный автомат, покрывающий автомат с рис. 1.
Практически необязательно перечислять все пары из G(Ei) и G( ).На каждом шаге достаточно смотреть, переводит ли некоторый входai A пару (si, sj) в разные классы эквивалентности . Если да, то на следующем шагеsiи sj следует развести по разным классам.
Пример.
Рассмотрим автомат с пятью состояниями:
|
Текуще- |
Следующее состояние |
Выход |
|
||||
|
есостоя- |
0 |
|
1 |
|
0 |
1 |
|
|
ние |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
s0 |
s1 |
|
s2 |
|
1 |
0 |
|
|
s1 |
s4 |
|
s2 |
|
0 |
0 |
|
|
s2 |
s3 |
|
s0 |
|
1 |
0 |
|
|
s3 |
s4 |
|
s0 |
|
0 |
0 |
|
|
s4 |
s4 |
|
s4 |
|
0 |
0 |
|
|
Имеем: |
|
|
|
|
|
|
|
|
s0E1s2, s1E1s3, s1E1s4, s3E1s4. |
|
|
|
|
|||
|
Это приводит к разбиению |
|
|
|
|
|||
: |
|
|
|
. |
|
|
|
|
|
Вход 1 переводит s3в s0, т.е. |
ν(s3,1) = s0; кроме того, |
||||||
ν(s4,1) = s4. Однакоs0 s4, |
такчтоs3 |
s4 |
(ибоΨ(s3,10) = 1 и |
|||||
Ψ(s4,10) = 0). |
|
|
|
|
|
|
|
|
Следующее разбиение π2состоит из классов эквивалентности
.
Дальнейшего измельчения не просходит, ибо ν переводит каждый элемент класса эквивалентности в тот же класс. Итак, состояния s0и s2 можно склеить в одно состояние ̅ , а состояния s1и s3 – в состояние ̅ . Состояние s4 получает пер-
вое обозначение s2. Новый минимальный автомат, покрывающий исходный автомат:
Следующее состояние |
|
Выход |
|||
0 |
1 |
|
0 |
1 |
|
|
|
|
|
|
|
̅ |
̅ |
̅ |
1 |
|
0 |
|
|
|
|
|
|
̅ |
̅ |
̅ |
0 |
|
0 |
|
|
|
|
|
|
̅ |
̅ |
̅ |
0 |
|
0 |
|
|
|
|
|
|
2.4.Автоматные функции и эксперименты с автоматами
2.4.1.Понятие ограниченной детерминированной функ-
|
ции\ |
|
Пусть даны |
— входной алфавит |
и |
|
— выходной алфавит. Обозначим и |
как |
множества все возможных последовательностей в алфавитах Aи B соответственно.
Определение 1. Отображение : → называется детерминированной функцией, если b(t)для любого t=1,2,… однозначно определяется поa(1),a(2),…,a(t).
Функция такая, что
будет g-функцией, если |
, то |
и |
|
если { |
,то |
. |
|
Определение |
2. Пусть |
заданаg-функция : → |
. Рас- |
смотрим произвольное входное слово ̅ |
. |
||
Определим |
функцию |
следующим образом: |
пусть |
a(1),a(2),…,a(t)— произвольная входная последовательность.
Рассмотрим |
. |
Тогда по- |
ложив |
|
при |
этом называется остаточной функцией φ по слову ̅ |
. |
|
Определение 3. Детерминированная функция : → называется ограниченно-детерминированной функцией, если у нее имеется лишь конечное число различных остаточных
функций. Рассмотрим автомат |
(A,S,B,φ, |
, ) где A,S,B — ко- |
|||||
нечные алфавиты (входной, выходной и состояния), |
: |
||||||
- переходная функция, |
|
: |
|
- выходная, |
- |
||
начальное состояние. |
|
|
|
|
|
||
Входом |
автомата |
служит |
|
последовательность |
|||
a(1),a(2),…,a(t) |
(конечная или бесконечная), выходом ав- |
||||||
томата служит последовательность |
, |
при этом автомат за- |
|||||
дается системой канонических уравнений: |
|
||||||
|
|
{ |
|
|
|
|
|
Определение 4. Отображение |
: |
→ |
называется авто- |
||||
матной функцией, если существует автомат, который реализует это отображение. Справедливо утверждение. Справедливо утверждение: функция является автоматной тогда и только тогда, когда она ограниченно детерминированная.
Пример: Пусть , а система канонических уравнений выглядит следующим образом:
{
Такой автомат осуществляет отображение и называется единичной задержкой.
