
Размещено на http://www.Allbest.Ru/
Введение
В данной курсовой работе рассматривается задача коммивояжера. Целью курсовой работы является решение задачи коммивояжера методом ветвей и границ.
Задача коммивояжера заключается в определении такой последовательности объезда городов, которая обеспечит минимальное время переезда, или минимальную стоимость проезда, или минимальное расстояние переезда.
Сейчас решение задачи коммивояжера необходимо во многих областях связанных с замкнутыми и при этом жестко связанными по времени системами, такими как: конвейерное производство, многооперационные обрабатывающие комплексы, судовые и железнодорожные погрузочные системы, перевозки грузов по замкнутому маршруту, расчет авиационных линий.
Поэтому данная проблема на современном этапе развития общества имеет не самое последнее по значимости место.
В коммерческой деятельности коммерсанты, торговые агенты постоянно проводят работу по поиску партнеров или клиентов для заключения договоров на поставку и покупку товаров. Для решения этих задач коммерсантам необходимо выезжать в командировки, выполнять вояж по целой сети городов как по нашей стране, так и за рубежом. Поскольку продолжительность командировки и транспортные расходы следует сокращать, то необходимо перед поездкой составить кратчайший маршрут, предусматривающий посещение каждого пункта только один раз, и вернуться обратно. Задача коммивояжера заключается в определении такой последовательности объезда городов, которая обеспечит минимальное время переезда, или минимальную стоимость проезда, или минимальное расстояние переезда.
Постановка задачи
Пусть
имеется п городов. Расстояния между
любой парой городов (i, j) известны и
составляют dij, где i=1, m; j=1, n; i≠j. Если
прямого маршрута сообщения между
городами не существует, а также для всех
i=j полагаем, что dij=∞. На этом основании
расстояния между городами удобно
представить в виде матрицы
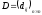 .
.

Рис. 1 - Неориентированный граф задачи коммивояжера
Если городам поставить в соответствие вершины графа (рис. 1), а соединяющим их дорогам дуги, то в терминах теории графов задача заключается в определении гамильтонова контура минимальной длины. Гамильтоновым контуром называется путь, проходящий через все вершины графа, у которого начальная вершина совпадает с конечной, а длина контура определяется суммой длин всех дуг, входящих в контур. Таким образом, необходимо построить кольцевой маршрут проезда всех городов минимальной длины, начиная с любого пункта и в любую сторону.
Поскольку
всего городов п, то коммивояжер, выехав
из заданного города, должен побывать в
остальных (n-1) городах только один раз.
Следовательно, всего существует (n-1)!
возможных маршрутов, среди которых один
или несколько – оптимальные. В большинстве
случаев можно предположить, что расстояние
между городами i и j является симметричным
и равно расстоянию от города j до города
i, т.е.
 .
Расстояния между городами запишем в
виде соответствующей матрицы и обозначим
ее через D. Если в задаче n городов, то D
является матрицей размером
.
Расстояния между городами запишем в
виде соответствующей матрицы и обозначим
ее через D. Если в задаче n городов, то D
является матрицей размером
 с неотрицательными элементами
с неотрицательными элементами
 ,
которые отображают длины дуг в сети
городов. При n=5 количество возможных,
вариантов маршрутов равно
,
которые отображают длины дуг в сети
городов. При n=5 количество возможных,
вариантов маршрутов равно
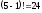 .
Расстояния между городами заданы
матрицей в табл. 1.
.
Расстояния между городами заданы
матрицей в табл. 1.
Таблица 1
|
i j |
1 |
2 |
3 |
4 |
5 |
|
1 |
∞ |
90 |
80 |
40 |
100 |
|
2 |
60 |
∞ |
40 |
50 |
70 |
|
3 |
50 |
30 |
∞ |
60 |
20 |
|
4 |
10 |
70 |
20 |
∞ |
50 |
|
5 |
20 |
40 |
50 |
20 |
∞ |
Маршрут можно представить в виде замкнутого контура, представляющего собой кольцевой маршрут, например, для графа, изображенного на рис. 1. Возможный вариант можно записать в виде совокупности соответствующих пар дуг:

Длина
 маршрута равна сумме соответствующих
длин дуг матрицы расстояний, тогда
целевую функцию можно записать так:
маршрута равна сумме соответствующих
длин дуг матрицы расстояний, тогда
целевую функцию можно записать так:

Для любого допустимого маршрута каждая строка и каждый столбец матрицы расстояний D содержат только по одному элементу. Решением задачи является определение кольцевого маршрута минимальной длины.
