
- •Гоувпо «Воронежский государственный технический
- •Университет»
- •Кафедра «Прикладная механика»
- •Методические указания
- •Печатается по решению редакционно-издательского совета Воронежского государственного технического университета
- •1. Цель расчетно - графических заданий
- •2. Выбор вариантов заданий
- •3. Задание № 1.
- •4. Задание № 2.
- •5. Задание № 3
4. Задание № 2.
РАСЧЕТ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
ПРИ КРУЧЕНИИ
Задача № 3
К
шкивам равномерно вращающегося стального
вала постоянного кругового сечения
(рис. 2.1) приложены заданные моменты
![]() ,
,![]() ,
,![]() и момент
и момент![]() .Исходные
данные взять из таблицы 2.1.
.Исходные
данные взять из таблицы 2.1.
Требуется:
1.
Из уравнения равновесия моментов сил,
приложенных к валу, определить момент
![]() на
ведущем шкиве.
на
ведущем шкиве.
2. Построить эпюру крутящих моментов.
3.
При значении допускаемого касательного
напряжения
![]() =80
МПа
определить диаметр вала сплошного
сечения из расчета на прочность и
округлить его величину до целого значения
в мм,
кратного
пяти.
=80
МПа
определить диаметр вала сплошного
сечения из расчета на прочность и
округлить его величину до целого значения
в мм,
кратного
пяти.
4. Построить эпюру углов закручивания сечений вала относительно крайнего левого сечения.
Величины
моментов
![]() даны вН*м,
размеры a,
b c метрах.
Принять модуль сдвига равным
даны вН*м,
размеры a,
b c метрах.
Принять модуль сдвига равным
![]() 8,0*104
МПа.
8,0*104
МПа.
Задача № 4
К
стальному валу, защемленному с двух
сторон (рис. 2.1), приложены два заданных
момента
![]() и
и![]() .
Коэффициент
.
Коэффициент![]() определяет отношение диаметра вала
определяет отношение диаметра вала![]() на участке с номеромi,
к
некоторому характерному диаметру
на участке с номеромi,
к
некоторому характерному диаметру
![]() ,
который следует определить.
,
который следует определить.
Требуется:
1. Раскрыть статическую неопределимость системы.
2. Построить эпюру крутящих моментов.
3.
При значении допускаемого относительного
угла закручивания
![]() =0,05
1/м
и модуле сдвига равном
=0,05
1/м
и модуле сдвига равном
![]() 8,0*104
МПа
определить
диаметр
8,0*104
МПа
определить
диаметр
![]() вала сплошного круглого сечения из
расчета на жесткость и округлить его
величину до целого значения в мм,
кратного
пяти.
вала сплошного круглого сечения из
расчета на жесткость и округлить его
величину до целого значения в мм,
кратного
пяти.
4. Построить эпюру максимальных касательных напряжений в поперечных сечениях вала.
Таблица 2.1
|
№ |
Моменты, кН*М |
Размеры, м |
|
| ||||
|
|
|
|
|
|
| |||
|
1 |
0,2 |
0,6 |
2,9 |
0,5 |
1,0 |
0,5 |
0,4 |
2,0 |
|
2 |
0,1 |
0,7 |
2,8 |
0,6 |
0,9 |
0,5 |
0,5 |
1,9 |
|
3 |
0,5 |
0,8 |
2,7 |
0,7 |
0,8 |
0,5 |
0,6 |
1,8 |
|
4 |
0,6 |
0,9 |
2,6 |
0,8 |
0,7 |
0,5 |
0,7 |
1,7 |
|
5 |
0,7 |
1,0 |
2,5 |
0,5 |
0,6 |
0,9 |
0,8 |
1,6 |
|
6 |
0,8 |
0,2 |
2,4 |
0,6 |
0,5 |
0,9 |
0,9 |
1,5 |
|
7 |
0,9 |
0,3 |
2,3 |
0,7 |
0,5 |
0,8 |
1,0 |
1,4 |
|
8 |
1,0 |
0,4 |
2,2 |
0,8 |
0,6 |
0,6 |
1,1 |
1,3 |
|
9 |
1,1 |
0,5 |
2,1 |
0,5 |
0,7 |
0,8 |
1,2 |
1,2 |
|
10 |
1,2 |
2,0 |
2,0 |
0,6 |
0,8 |
0,6 |
1,3 |
1,1 |
|
11 |
1,3 |
1,9 |
1,9 |
0,7 |
0,9 |
0,4 |
1,4 |
1,0 |
|
12 |
1,4 |
1,8 |
1,8 |
0,8 |
1,0 |
0,2 |
1,5 |
0,9 |
|
13 |
1,5 |
1,7 |
1,7 |
0,9 |
0,5 |
0,6 |
1,6 |
0,8 |
|
14 |
1,6 |
1,6 |
1,6 |
1,0 |
0,6 |
0,4 |
1,7 |
0,7 |
|
15 |
1,7 |
1,5 |
1,5 |
0,5 |
0,7 |
0,8 |
1,8 |
0,6 |
|
16 |
1,8 |
1,4 |
1,4 |
0,6 |
0,8 |
0,6 |
1,9 |
0,5 |
|
17 |
1,9 |
1,3 |
1,3 |
0,7 |
0,9 |
0,4 |
2,0 |
0,4 |
|
18 |
2,0 |
1,2 |
1,2 |
0,8 |
1,0 |
0,2 |
0,4 |
2,0 |
|
19 |
2,1 |
1,1 |
1,1 |
0,9 |
0,5 |
0,6 |
0,5 |
1,9 |
|
20 |
2,2 |
2,9 |
1,0 |
1,0 |
0,6 |
0,4 |
0,6 |
1,8 |
|
21 |
2,3 |
2,8 |
0,9 |
0,5 |
0,7 |
0,8 |
0,7 |
1,7 |
|
22 |
2,4 |
2,7 |
0,8 |
0,6 |
0,8 |
0,6 |
0,8 |
1,6 |
|
23 |
2,5 |
2,6 |
0,7 |
0,7 |
0,5 |
0,8 |
0,9 |
1,5 |
|
24 |
2,6 |
2,5 |
0,6 |
0,8 |
0,6 |
0,6 |
1,0 |
1,4 |
|
25 |
2,7 |
2,4 |
0,5 |
0,9 |
0,7 |
0,4 |
1,1 |
1,3 |
|
26 |
2,8 |
2,3 |
0,4 |
1,0 |
0,8 |
0,2 |
1,2 |
1,2 |
|
27 |
2,9 |
2,2 |
0,3 |
0,5 |
0,9 |
0,6 |
1,3 |
1,1 |
|
28 |
3,0 |
2,1 |
0,2 |
0,4 |
0,8 |
0,5 |
1,4 |
1,2 |
|
29 |
3,1 |
2,0 |
0,2 |
0,3 |
0,7 |
0,6 |
1,3 |
1,1 |
|
30 |
2,3 |
2,2 |
1,2 |
0,6 |
0,7 |
9,9 |
1,9 |
0,9 |
Р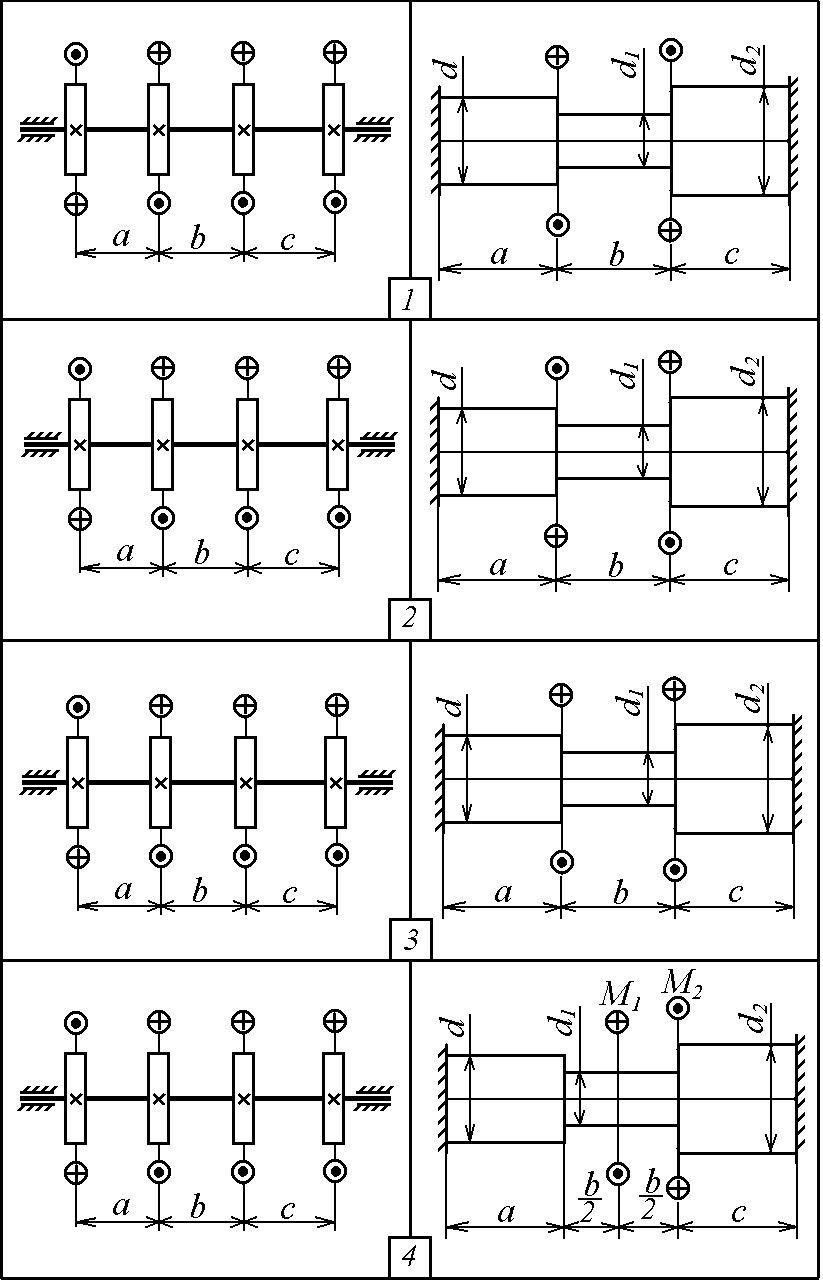 ис.
2.1
ис.
2.1
Р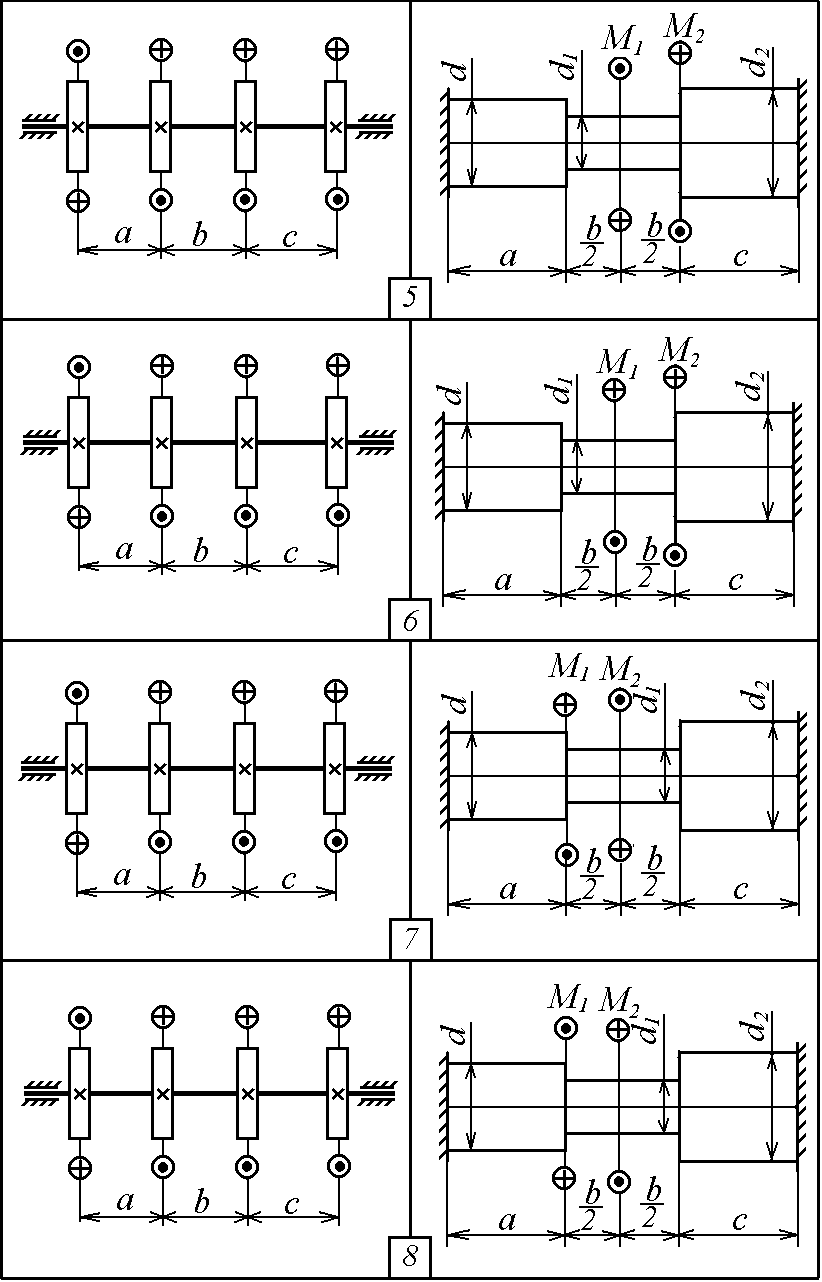 ис.
2.1. Продолжение
ис.
2.1. Продолжение
Р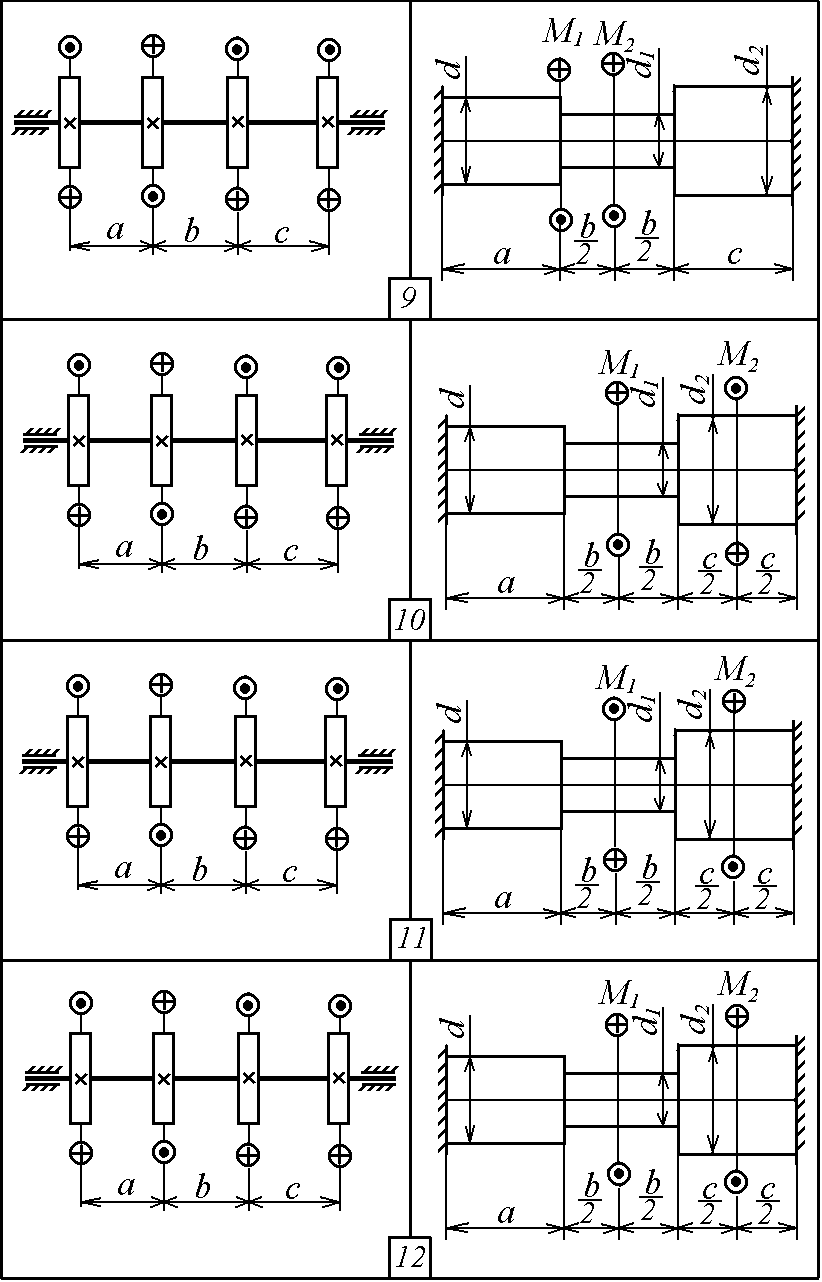 ис.
2.1. Продолжение
ис.
2.1. Продолжение
Р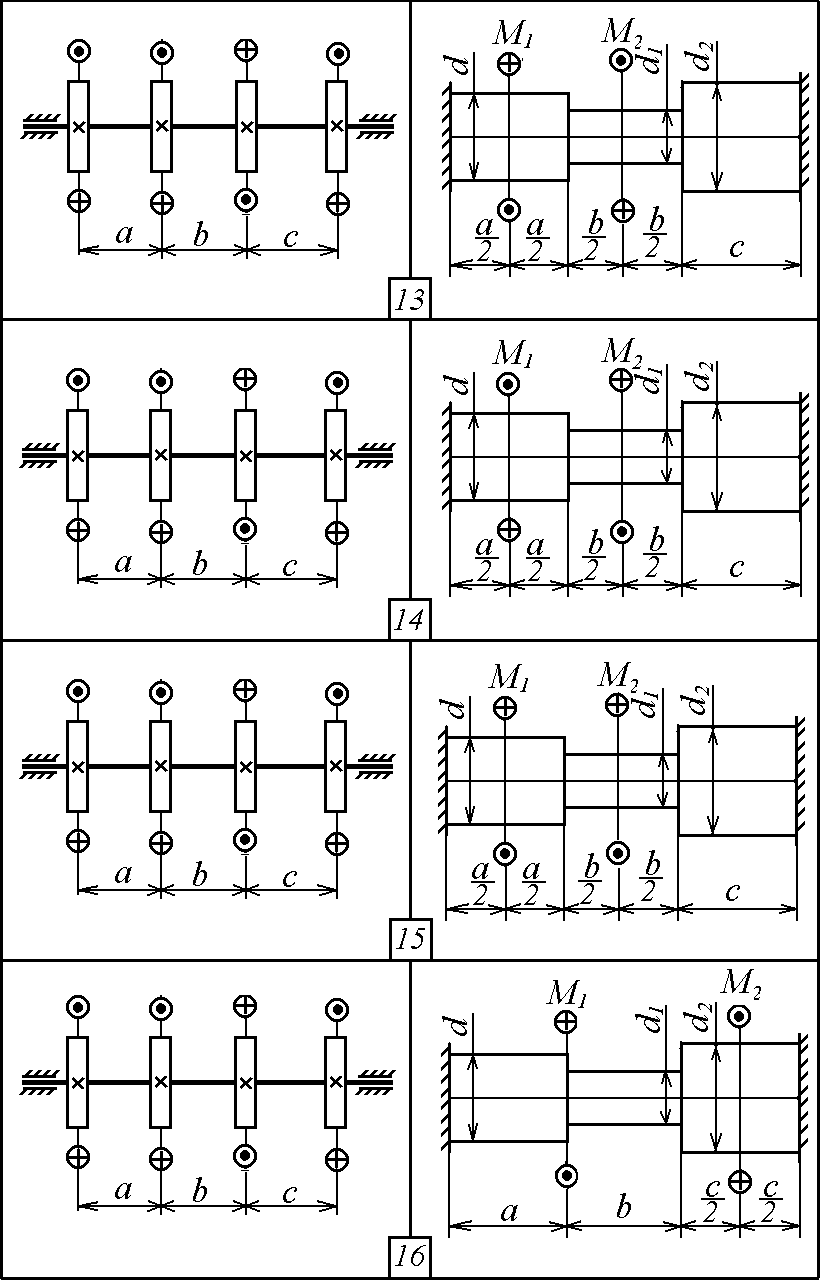 ис.
2.1. Продолжение
ис.
2.1. Продолжение
Р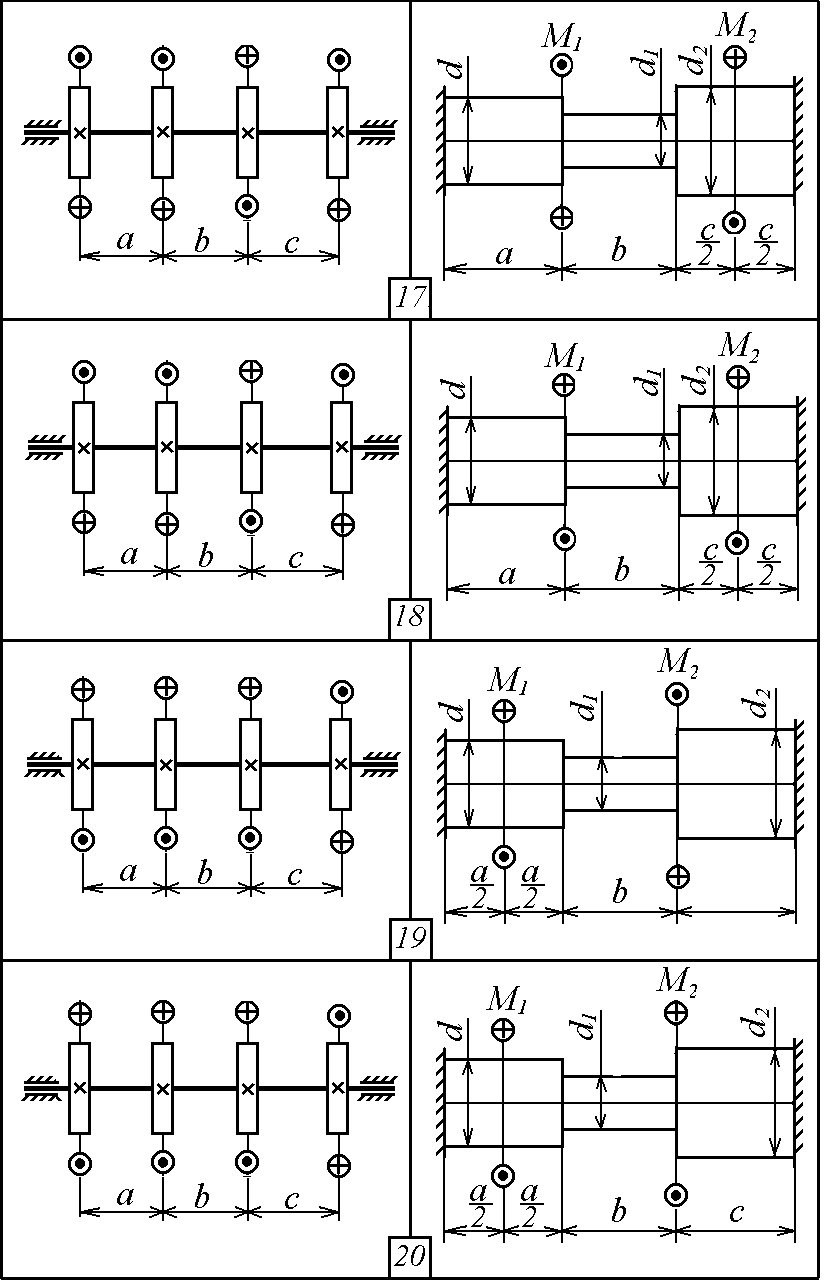 ис.
2.1. Продолжение
ис.
2.1. Продолжение
Р ис.
2.1. Продолжение
ис.
2.1. Продолжение
Р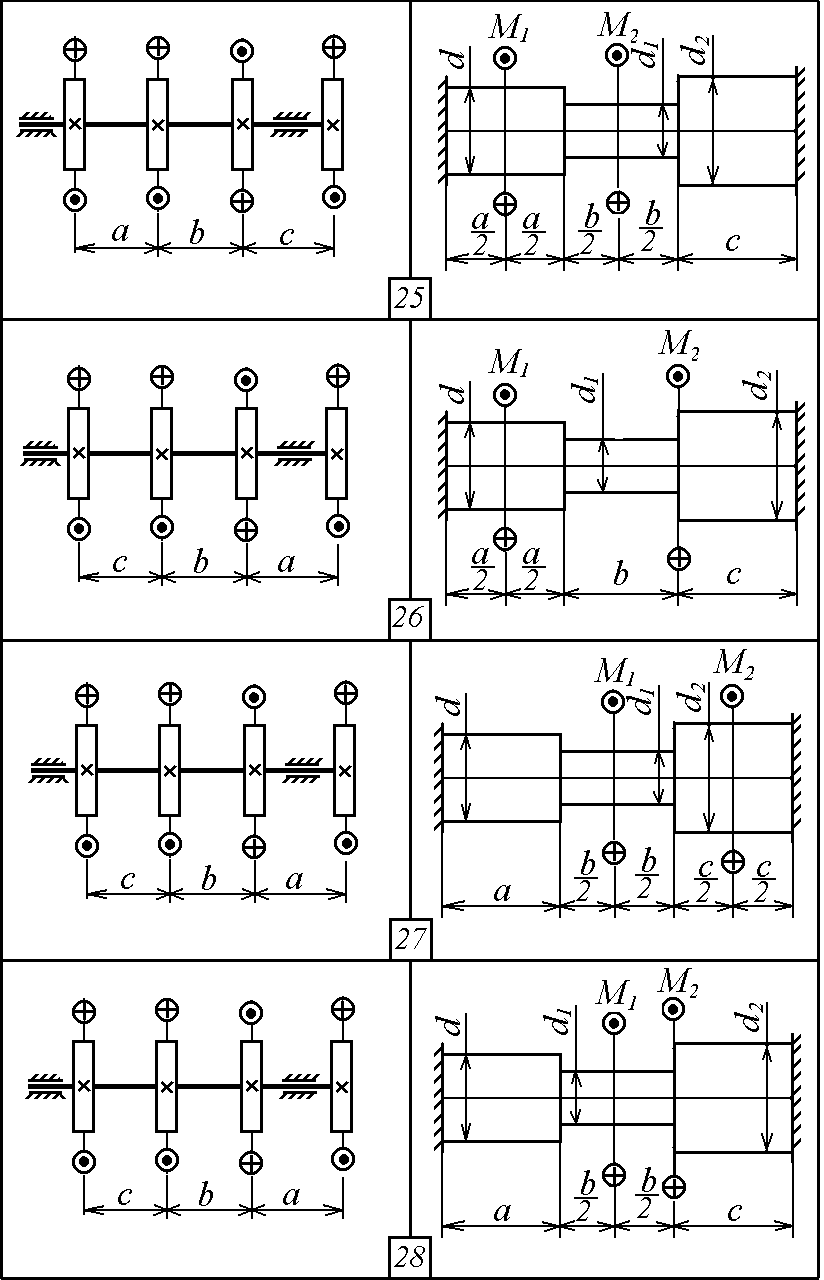 ис.
2.1. Продолжение
ис.
2.1. Продолжение
Р ис.
2.1. Продолжение
ис.
2.1. Продолжение
Р ис.
2.1. Окончание
ис.
2.1. Окончание
