Последовательное соединение элементов r, l, с

на рис. 3.10 приведена схема с последовательным соединением элементов элементов R, L, C.

Рис. 3.10

Согласно второму закону Кирхгофа для мгновенных значений u=u_R+u_L+u_C.

Второй закон Кирхгофа также справедлив и для векторов, изображающих мгновенные значения:

где Z–комплексное сопротивлениецепи, записанное в алгебраической форме записи, где активное сопротивление записывают в виде действительного числа, а реактивные сопротивления – в виде мнимого числа, причем, индуктивное сопротивление положительно, а емкостное - отрицательно.

В показательной форме записи:

где z=|Z| и называетсяполным сопротивлениемцепи, а φ - угол сдвига фаз:

.

Из выражения, записанного для комплексного сопротивления Z видно, что сопротивления в цепи с последовательным соединением элементов связаны в прямоугольный треугольник (рис. 3. 11).

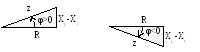
а) б)

Рис. 3.11

Из треугольника сопротивлений (рис. 3.11) следует:

где X- реактивное сопротивление цепи может быть больше или меньше нуля.

Векторной диаграммой называется совокупность векторов токов и напряжений, изображающих синусоидальные электрические величины исследуемой цепи.

На рис. 3.12 приведены векторные диаграммы цепи при разных соотношениях сопротивлений X_L иX_C.

ПриU_L>U_C. ПриU_L<U_C.

Построение векторной диаграммы начинают с вектора тока, так как он одинаков для всех элементов. Напряжение на активном элементе совпадает по фазе с током, напряжение на индуктивном элементе опережает ток на 90^О, а на емкостном элементе напряжение отстает от тока на 90^О. Затем складывают векторы напряжений элементов в соответствии со вторым законом Кирхгофа и получают напряжение, приложенное к цепи:

.

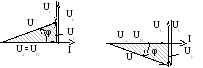
φ>0 φ<0

a) б)

Рис. 3.12

Для этого из конца вектора напряжения проводят вектор напряжения, затем из конца вектора напряженияпроводят вектор напряжения. Вектор, соединяющий начало первого вектора и конец третьего, равен вектору напряжения, приложенному к цепи. Указывают на диаграмме угол сдвига фаз ветви: φ=ψ_u-ψ_i. Угол φ равен аргументу комплексного сопротивления ветви.

Так как векторы _Lи_Cнаправлены вдоль одной оси, но в противоположные стороны, то их векторную сумму можно заменить алгебраической разностью

,

где U_p– реактивная составляющая напряжения, приложенного к цепи.

На рис. 3.12 заштрихованные треугольники принято называть треугольниками напряжений.

Из треугольника напряжений следует:

.

Или

Если стороны прямоугольного треугольника напряжений (рис. 3.12) умножить на общий ток I, то получим треугольник мощностей (рис. 3.13, а, б).

а) б)

Рис. 3.13

Гипотенуза треугольника есть полная мощность цепиS:

катеты: - активная мощность,

- реактивная мощность.

По теореме Пифагора

Единицы измерения мощности: [S] – ВА, [P] – Вт, [Q] – ВАр.

Угол сдвига фаз (рис. 3.13):