3. Математическая модель электромеханической системы подчиненнго управления с упругой механической связью

На рис. 3 показана принципиальная схема исследуемой электромеханической системы, в которой приняты следующие обозначения: ТГ – тахогенератор (– напряжение ТГ,– согласующее сопротивление для сигнала обратной связи по скорости); ЭД – электродвигатель ( – частота вращения ЭД, – ток якоря ЭД); Р – редуктор; ТП – тиристорный преобразователь; ДТ – датчик тока ( ,– аналогично ТГ); БТО – блок токоограничения;– напряжение задания; РС – регулятор скорости ( z_рс – операторное сопротивление в цепи ОС регулятора скорости, – согласующее сопротивление для входного напряжения, – напряжение на выходе РС); РТ – регулятор тока ( z_рт, ,– аналогично РС); СУ – система управления, формирующая управляющие сигналы для ТП; – жесткость механической связи между ЭД и исполнительным механизмом.

Классический анализ систем подчиненного управления предполагает расчет по одномассовой структурной схеме, характеристики которой хорошо изучены и подробно описаны, например, в [4, 5, 9]. Широкое развитие в теории автоматического управления получили методы анализа и синтеза динамических структур ЭП, основанные на использовании исходного математического описания в виде нормированной структурной схемы [5]. Наглядный и универсальный характер подобного описания облегчает исследование динамических свойств графическими, частотными методами и путем моделирования на ЭВМ.

Расчетная структурная схема в абсолютных единицах, соответствующая исследуемой ЭМС (рис. 3), и НСС для одномассовой системы показана на рис. 4. Аналогичные схемы для двухмассовой ЭМС, учитывающие упругость механической части электропривода, показаны на рис. 5. Приняты следующие обозначения: ,– соответственно, постоянные времени датчика тока и тахогенератора;– постоянная времени тиристорного преобразователя;,,,– коэффициенты передачи и нормированные постоянные времени для регуляторов тока и скорости;,– передаточные функции регуляторов контуров скорости и тока;, T_я – нормированное значение сопротивления и постоянная времени цепи якоря;, В*с – коэффициент, определяющий взаимосвязь между ЭДС двигателя и его частотой вращения при постоянном магнитном потоке, вычисляется по паспортным данным электродвигателя.

Суммарный момент инерции определяется как сумма момента инерции электродвигателя и момента инерции исполнительного механизма, приведенного к валу ЭД. Нормированное значение сопротивления цепи якоряопределяется по формуле [5]:

. (10)

Суммарная механическая постоянная времени , с, определяется как сумма механических постоянных времени первой и второй масс соответственно. – постоянная времени жесткости;,, – соответственно: коэффициенты внешнего трения на первой массе, второй массе и внутреннего трения в передаче.

Формулы для определения указанных параметров:

;; (11)

; (12)

;; (13)

, (14)

где  J₁, J₂– приведенные моменты инерции первой и второй масс;

_н, M_н– номинальные частота вращения и момент ЭД;

a₁, a₂– размерные коэффициенты связи между моментами внешнего трения M_fi и скоростями вращения масс_i;

_вт– коэффициент внутреннего демпфирования.

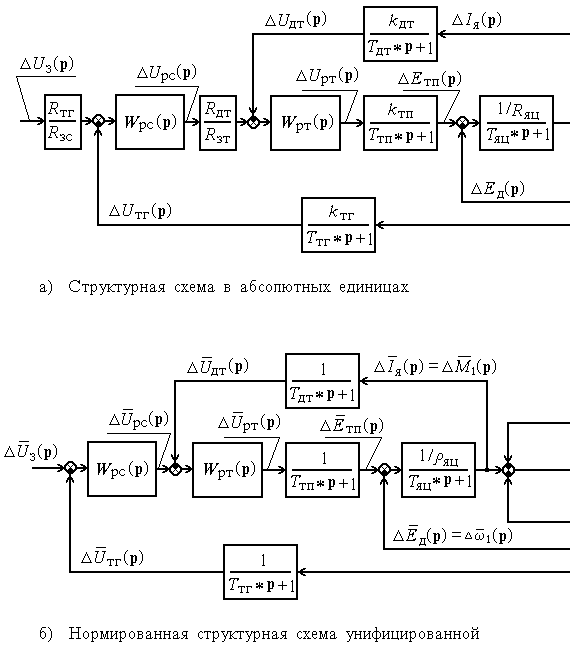
Рис. 5. Структурные схемы упругой двухмассовой

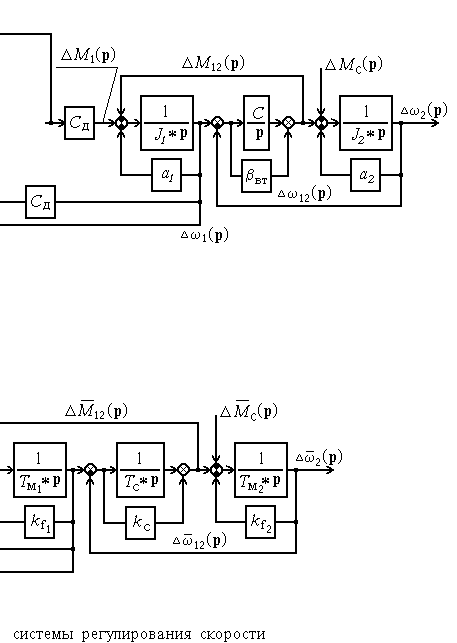
системы подчиненного управления.

, (15)

где  _вт– логарифмический декремент затухания колебаний; согласно [8], принимает значения от 0.1 до 0.3;

₁₂– собственная частота колебаний двухмассовой ЭМС.