
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ФГБОУ ВПО «ВГТУ», ВГТУ)
УЧЕБНО-ЛАБОРАТОРНЫЙ ЦЕНТР КАФЕДРЫ ФИЗИКИ
Методические указания к выполнению лабораторной работы
«Изучение эффекта Холла в полупроводниках»
Для студентов всех направлений (специальностей)
очной формы обучения
Воронеж 2013
Составители: канд. физ.-мат. наук В.С. Железный, канд. физ.-мат. наук Е.А. Косякова.
УДК 531.07
Методические указания к выполнению лабораторной работы «Изучение эффекта Холла в полупроводниках». Для студентов всех направлений (специальностей) / Воронеж. гос. техн. ун-т. Сост. В.С. Железный, Е.А. Косякова. Воронеж, 2005. с.
Методические указания содержат краткий теоретический материал и описание лабораторной работы ”Изучение эффекта холла в полупроводниках” по разделу общего курса физики ”Физика твердого тела”, выполняемых в учебных лабораториях ВГТУ.
Пособие предназначено для студентов технического профиля второго курса всех направлений (специальностей) дневной формы обучения.
Ил. 4. Табл. 1. Библиогр. 4 назв.
Рецензент канд. техн. наук, доцент М. Н. Гаршина
Ответственный за выпуск зав. кафедрой Физики,
канд. физ.-мат. наук, профессор Т.Л. Тураева
Издаётся по решению редакционно-издательского совета Воронежского государственного технического университета
©Воронежский государственный
технический университет, 2013
Изучение эффекта холла в полупроводниках
Цель работы: исследовать зависимость ЭДС Холла от силы тока и величины индукции магнитного поля; определить концентрацию и тип носителей тока в полупроводнике путем измерения ЭДС Холла датчика.
Принадлежности: установка для изучения эффекта Холла ФПК-08.
Теоретическое введение
В 1879 году Эдвин Герберт Холл, будучи молодым студентом, открыл неожиданный эффект. Он обнаружил, что если поместить тонкую золотую пластинку в магнитное поле, направленное перпендикулярно плоскости этой пластинки, и пропустить через нее электрический ток, то в направлении, перпендикулярном направлению и магнитного поля, и тока, возникает разность потенциалов. Это явление получило название эффекта Холла. Оно является одним из так называемых гальваномагнитных явлений, возникающих при одновременном действии на вещество магнитного и электрического полей.
Эффектом Холла
называется возникновение в металле или
полупроводнике электрического поля
![]() ,
перпендикулярного току в образце и
внешнему магнитному полю.
,
перпендикулярного току в образце и
внешнему магнитному полю.
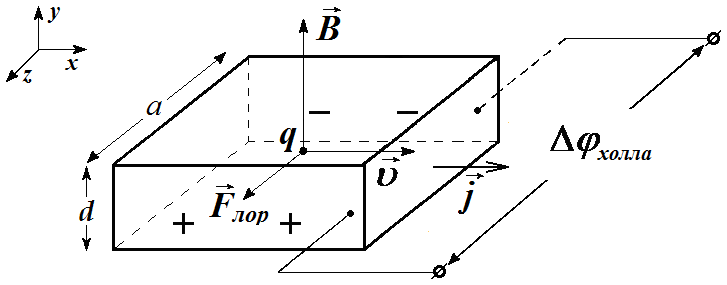
Рис. 1. Датчик Холла дырочного типа проводимости.
Этот эффект
объясняется следующим: если через
полупроводниковый или металлический
образец (рис.1) пропустить электрический
ток, плотностью
![]() (вдоль оси x),
и одновременно поместить его в магнитное
поле индукцией
(вдоль оси x),
и одновременно поместить его в магнитное
поле индукцией
![]() (направленное вдоль оси y),
носители заряда
(направленное вдоль оси y),
носители заряда
![]() ,
будут испытывать действие силы Лоренца
(вдоль оси z):
,
будут испытывать действие силы Лоренца
(вдоль оси z):
![]() (1)
(1)
Направление этой силы перпендикулярно и скорости движения зарядов, и направлению магнитного поля. Максимальна она в случае, когда магнитное поле перпендикулярно направлению тока в образце.
Скорость носителей заряда определяется плотностью тока, протекающего через образец:
![]() (2)
(2)
где n
- концентрация свободных носителей
заряда в образце,
![]() - их дрейфовая скорость. Сила и плотность
тока связаны соотношением:
- их дрейфовая скорость. Сила и плотность
тока связаны соотношением:
![]() (3)
(3)
![]() (4)
(4)
где d - толщина, a - ширина исследуемой пластинки.
Под действием силы Лоренца носители заряда противоположных знаков будут сдвигаться к противоположным граням образца. Это движение будет продолжаться до тех пор, пока возникшее при разделении зарядов электрическое поле не скомпенсирует действие силы Лоренца:
![]() (5)
(5)
Разность потенциалов, возникающая при этом вдоль оси z, называется холловской разностью потенциалов (или ЭДС Холла) и равна:
![]() (6)
(6)
В рассмотренном
случае (рис.1)
![]() и
и
![]() перпендикулярны друг другу, следовательно
в скалярной форме уравнение (5) принимает
вид:
перпендикулярны друг другу, следовательно
в скалярной форме уравнение (5) принимает
вид:
![]() (7)
(7)
С учетом приведенных выше формул получаем:
![]() (8)
(8)
![]() (9)
(9)
Константа
![]() называется постоянной Холла. Знак
постоянной и, следовательно, направление
ЭДС Холла зависят от знака носителей
тока. Для свободных электронов постоянная
Холла отрицательна. Положительная
постоянная Холла означает, что носителями
тока являются положительные заряды.
Т.о., постоянная Холла
называется постоянной Холла. Знак
постоянной и, следовательно, направление
ЭДС Холла зависят от знака носителей
тока. Для свободных электронов постоянная
Холла отрицательна. Положительная
постоянная Холла означает, что носителями
тока являются положительные заряды.
Т.о., постоянная Холла
![]() для металлов и полупроводников
электронного типа (n-типа),
для металлов и полупроводников
электронного типа (n-типа),
![]() для полупроводников дырочного типа
(р-типа).
для полупроводников дырочного типа
(р-типа).
Определив коэффициент Холла, можно рассчитать концентрацию основных носителей заряда в исследуемом образце.
Выражение (9) для постоянной Холла получено в предположении, что все носители тока имеют одинаковую скорость движения, которая к тому же не изменяется при движении носителей тока в веществе. Такое допущение справедливо для металлов, в которых ток переносится электронами, обладающими одной и той же энергией (энергией Ферми). Мы не учли, следовательно, что при движении в реальном веществе носители тока испытывают столкновения и потому рассеиваются на примесях, на колебаниях решетки. Учет рассеяния носителей тока в веществе приводит к несколько иному выражению для R, вид которого зависит от механизма рассеяния. Например, для чистых полупроводников с собственной проводимостью, когда рассеяние происходит главным образом на тепловых колебаниях решетки, для постоянной Холла получается выражение:
![]() (10)
(10)
Если основное значение имеет рассеяние на ионизированных атомах примеси (т.е. в примесном полупроводнике), то справедливо выражение:
![]() (10')
(10')
Для полупроводников со смешанной проводимостью, если концентрации электронов и дырок сравнимы друг с другом, постоянная Холла вычисляется по формуле:
 (10')
(10')
где
![]() - концентрации дырок и электронов
соответственно,
- концентрации дырок и электронов
соответственно,
![]() - подвижности дырок и электронов.
- подвижности дырок и электронов.
Подвижностью носителей тока называется величина, численно равная дрейфовой скорости носителей заряда, которую они приобретают в электрическом поле с напряженностью 1 В/м:
![]() (11)
(11)
Подвижностью
свободных носителей заряда и их
концентрацией определяется
электропроводность материала
![]() .
В частности, тип проводимости чистого
полупроводника принято определять по
соотношению подвижностей электронов
и дырок. Если подвижность, к примеру,
дырок оказывается больше подвижности
электронов, то вещество проявляет
свойства дырочного полупроводника.
.
В частности, тип проводимости чистого
полупроводника принято определять по
соотношению подвижностей электронов
и дырок. Если подвижность, к примеру,
дырок оказывается больше подвижности
электронов, то вещество проявляет
свойства дырочного полупроводника.
Следует заметить, что приведенные выше расчеты справедливы для слабых магнитных полей. В сильных полях наблюдается не просто отклонение носителей зарядов к боковым граням образца, но и их "закручивание" вокруг линий индукции магнитного поля. Критерием применимости формулы (8) является выражение:
![]() (12)
(12)
Рассмотренный эффект Холла, причиной которого является действие на движущиеся в магнитном поле заряды силы Лоренца, называется классическим эффектом Холла. Как следует из формулы (8), для классического эффекта Холла характерна линейная зависимость ЭДС от величины магнитного поля. Опыт между тем показывает, что в природе есть вещества, для которых эта зависимость нелинейна. Это свидетельствует о существовании другой причины эффекта Холла, которая может быть понята только с позиций квантовой теории твердого тела. В полупроводниках эффект Холла имеет в основном классическую природу, и для его описания справедливо выражение (8).
Эффект Холла сопровождается другим гальваномагнитным явлением - эффектом Эттингсгаузена, который заключается в возникновении в полупроводнике или металле градиента температур, в направлении, перпендикулярном току в образце и внешнему магнитному полю. Кратко его можно объяснить следующим образом: под действием силы Лоренца носители заряда движутся к боковым граням (как это было описано выше). При этом скорость их движения будет неодинаковой вследствие статистического разброса. На заряды, имеющие различную скорость магнитное поле будет действовать по-разному - быстрые носители заряда будут сильнее отклоняться и при это отдавать свою энергию кристаллической решетке, нагревая соответствующую грань. Медленные носители заряда у противоположной грани будут, наоборот, оттягивать энергию у кристаллической решетки, охлаждая ее. Тем самым противоположные грани образца будут иметь различную температуру.
Метод, основанный на использовании эффекта Холла, является наиболее эффективным современным способом определения типа проводимости полупроводников, а также концентрации свободных носителей заряда. Величина константы Холла позволяет сделать заключение о количестве примесей в полупроводнике.
Эффект Холла широко применяют при создании различных приборов и устройств в современной технике. В частности, на основе эффекта Холла работают некоторые виды ионных реактивных двигателей, датчики Холла - приборы, предназначенные для измерения величины магнитного поля, в том числе и для бесконтактного измерения магнитных полей.
Датчики Холла получили большое распространение в бесколлекторных, или вентильных, электродвигателях (сервомоторах). Датчики закрепляются непосредственно на статоре двигателя, они выступают в роли ДПР (датчика положения ротора). ДПР реализует обратную связь по положению ротора.
При помощи датчика Холла можно измерять любую физическую величину, которая однозначно связана с магнитным полем, например, силу тока. Амперметры на основе эффекта Холла рассчитаны на измерение токов до 100 кА.
Датчики Холла применяют в аналоговых перемножающих устройствах; при этом токи, пропорциональные перемножаемым величинам, используются один для питания датчика, другой - для создания магнитного поля. ЭДС Холла при этом оказывается пропорциональной произведению этих величин.
Кроме того, датчики Холла применяют в измерителях линейных и угловых перемещений, а также в измерителях градиента магнитного поля, магнитного потока и мощности электрических машин, в бесконтактных преобразователях постоянного тока в переменный. Также датчики Холла входят в конструкцию воспроизводящих головок систем звукозаписи.
