Расчетные задания
Задача 1.
Периодический сигнал f(t)разложить в тригонометрический ряд Фурье. Вычертить графики сигналаf(t)и частичных суммS1(t),S2(t)ряда Фурье.
1.1. f(t) = | t | – 1 на [-2; 2],f(t + 4) = f(t).
1.2. f(t) = 2 + | t| на [-2; 2],f(t + 4) = f(t).
1.3. f(t) = | 1 – t2 |на [-1; 1],f(t + 2) = f(t).
1.4. f(t) = 1 – | t |на [-3; 3],f(t + 6) = f(t).
1.5.
.
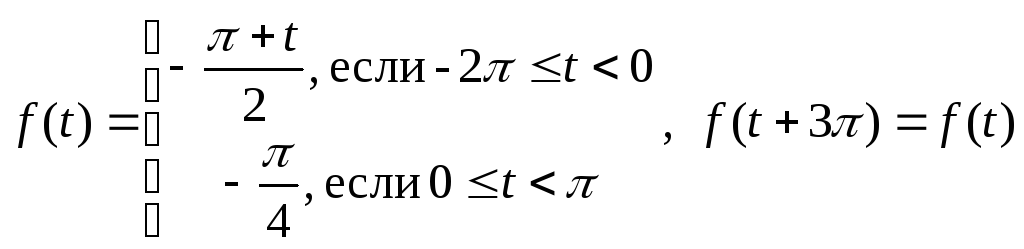f(t) = t2 + t на [-2 ; 2], f(t + 4) = f(t).
.
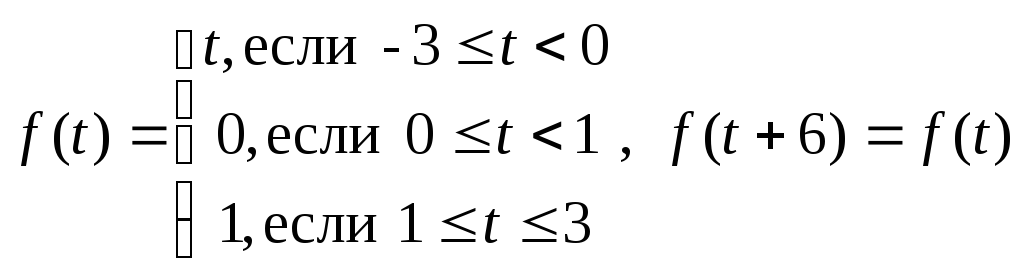1.8. f(t) = (t – 1) 2 на [-1; 1], f(t + 2) = f(t).
1.9.
.
1.10. f(t) = t2+1 на [-2;2], f(t + 4) = f(t).
1.11.
.
1.12.
.
1.13.
.
1.14. f(t) = 1 – 2t на [-2 ; 2], f(t + 4) = f(t).
1.15.
.
1.16.
.
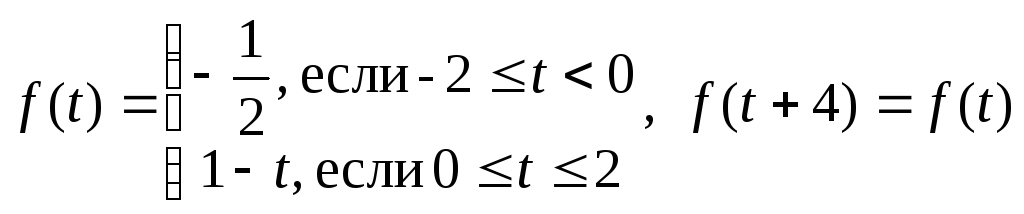1.17.
.
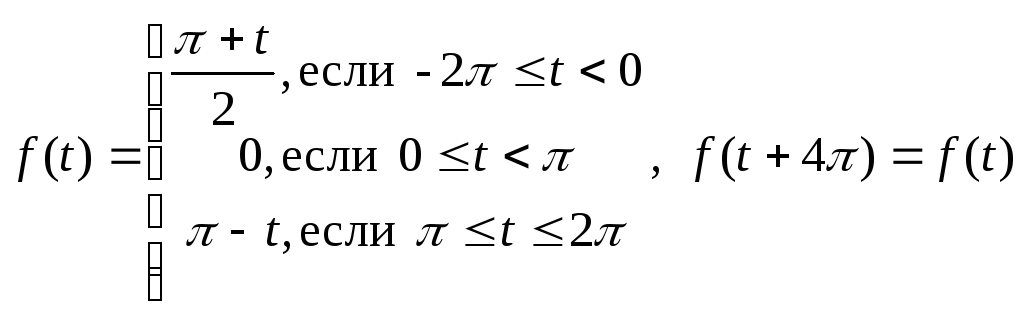1.18.
.
1.19.
.
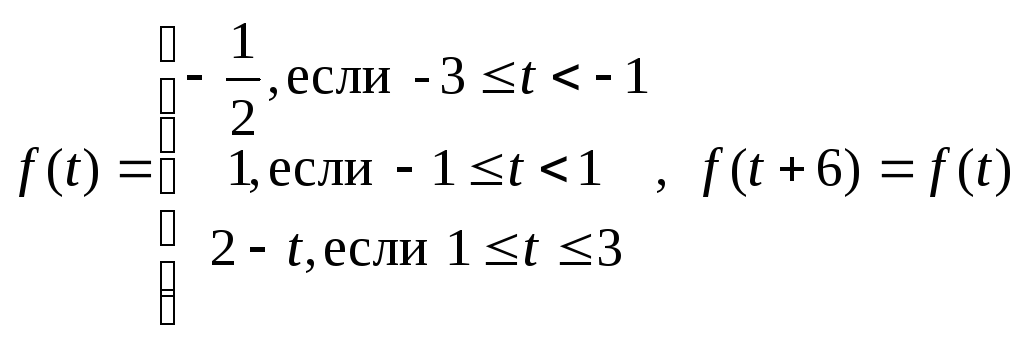1.20.
.
1.21.
.
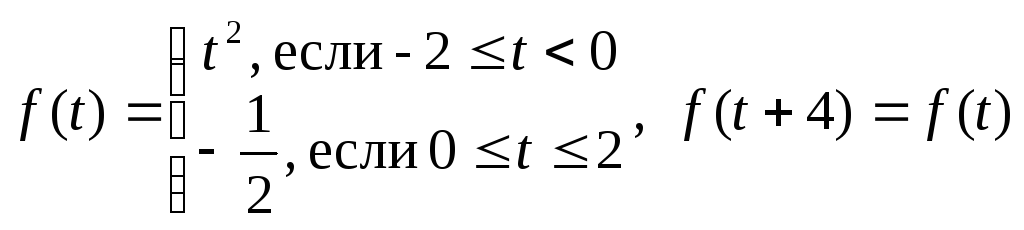1.22. f(t) = t - t2 на [-2 ; 2], f(t + 4) = f(t).
1.23.
.
1.24.
1.25 f(t)= t 2 – 2t + 2 на [-3; 3], f(t + 6) = f(t).
Задача 2.
Найти аналитическое выражение периодического тока I(t) определенного осциллограммой (см. рисунок). Записать ряд Фурье в действительной форме для I(t).
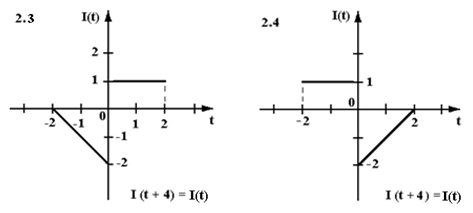
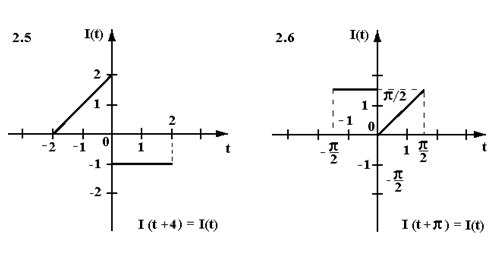
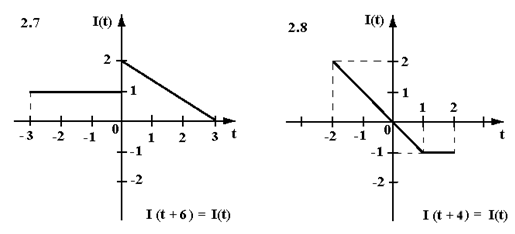
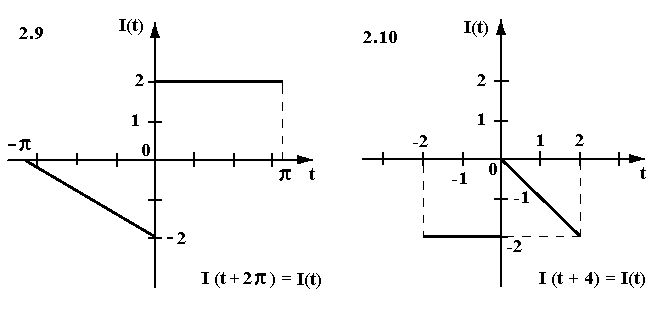
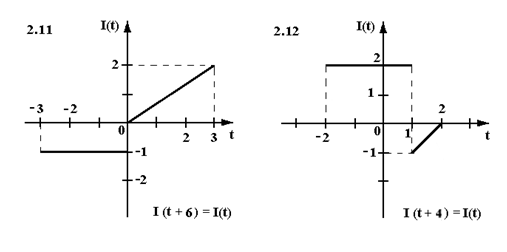
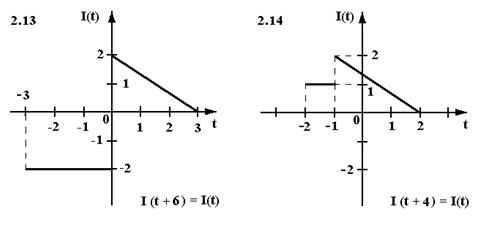
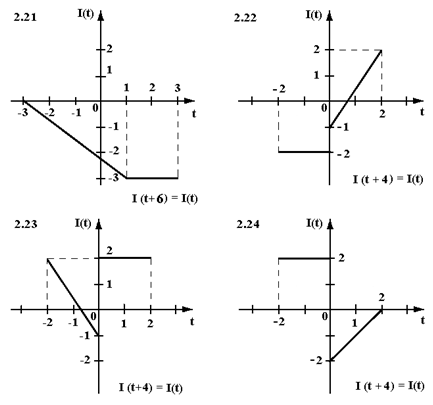
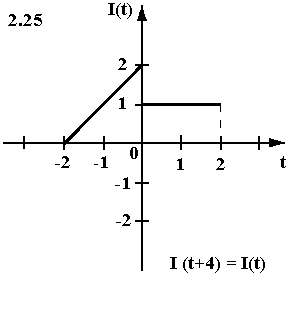
Задача 3.
Продолжая функцию f(t) четным или нечетным образом, разложить ее в ряд Фурье в № 3.1 – 3.12 по синусам , в № 3.12 – 3.25 по косинусам.
3.1. f(t) = t2 + tна [-1 ; 0].
3.2.
.
3.3.
.
3.4.
.
3.5.
.
3.6.
.
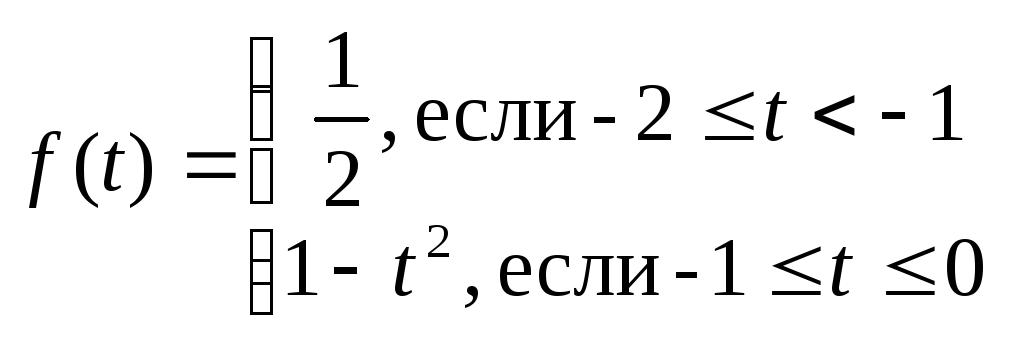3.7. f(t)
= t2 + 1,
если 0
t
2.
3.8.
.
3.9.
.
3.10. f(t)
= - t2 +
1, если 1
t
2.
3.11.
.
3.12. f(t)
= -t2 + t
– 2, если 0
t
1.
3.13.
.
3.14.
.
3.15.
.
3.16. f(t)
= t2 + t,
если -1
t
0.
3.17.
.
3.18. f(t)
= (t – 1)2,
если 0
t
1.
3.19.
.
3.20.
.
3.21. f(t)
= t2+ 1, если
0
t
2
.
3.22.
.
3.23. f(t)=-t2 +
t– 2, если 0
t
2.
3.24.
.
3.25. f(t)
= -t2+ 2, если
0
t
1.
Задача 4.Сигналf(t)представить рядом Фурье в комплексной форме. Воспользовавшись полученным разложением, записать ряд Фурье в действительной форме. Построить графики спектров {|Cn|} и {An}.
4.1.
.
4.2.
f(t) = ch 2t,
если -
t
<
,f(t +
)
= f(t).
4.3.
f(t) = sh 4t,
если -
t
<
,f(t +
)
= f(t).
4.4.
f(t) = ch
,
если -
t
<
, f(t +2
)
= f(t).
4.5.
f(t) = sh
,если
-
t
<
,
f(t + 2
)
= f(t).
4.6.
f(t) = ch 2t
+ e2t,
если 0
t<
,
f(t +
)
= f(t).
4.7.
f(t) = e-t,
если
-1
t
<1, f(t
+ 2) =
f(t).
4.8.
4.9.
f(t) = t –
1, если -1
t
<1, f(t + 2)
= f(t).
4.10.
f(t) = t – t2,
если -1
t
<1, f(t + 2)
= f(t).
4.11.
f(t) = et,
если -
t<
,
f(t + 2
)
= f(t).
4.12.
f(t) = 2
+ | t |,
если -1
t
<1, f(t
+ 2) = f(t).
4.13.
.
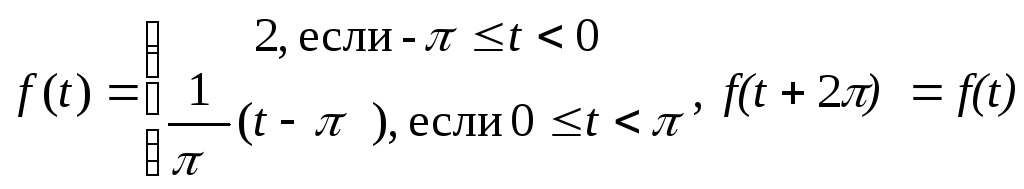4.14.
f(t) = sh 2t
– e2t,
если 0
t<
,
f(t +
)
= f(t).
4.15.
f(t) =
sin t,
если -
t<
,f(t +
)
= f(t).
4.16.
f(t) = t2
– 2t
+ 2, если -2
t<2,
f(t + 4)
= f(t).
4.17.
.
4.18.
f(t) =
cos t,
если 0
t<
,
f(t +
)
= f(t).
4.20
f(t) =
cos
,
если 0
t<3
,
f(t + 3
)
= f(t).
4.21
f(t) = 1
– | t |, если -1
t<1,
f(t + 2)
= f(t).
4.22
f(t) =
cos
,
если 0
t<4
,
f(t + 4
)
= f(t).
4.23.
.
4.24.
.
4.25.
f(t) = 2t,
если -2
t<2,
f(t + 4) =
f(t).
Задача 5.
Для импульса f(t) найти спектральную
плотность F(
)
и записать интеграл Фурье в комплексной
и действительной формах.
5.1.
.
5.2.
.
5.3.
.
5.4.
.
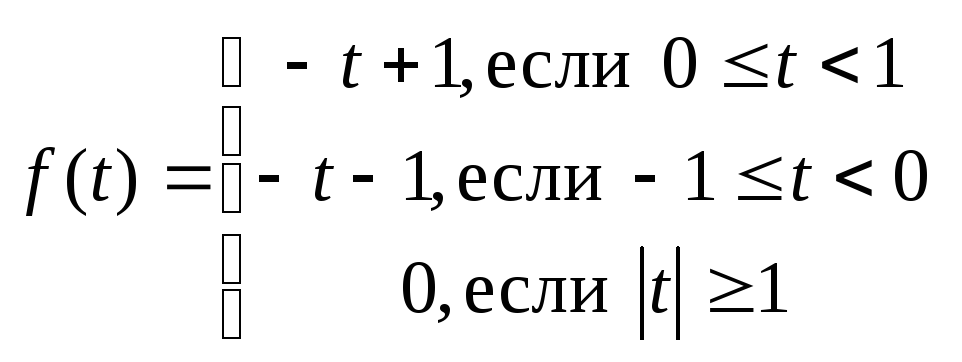5.5.
.
5.6.
.
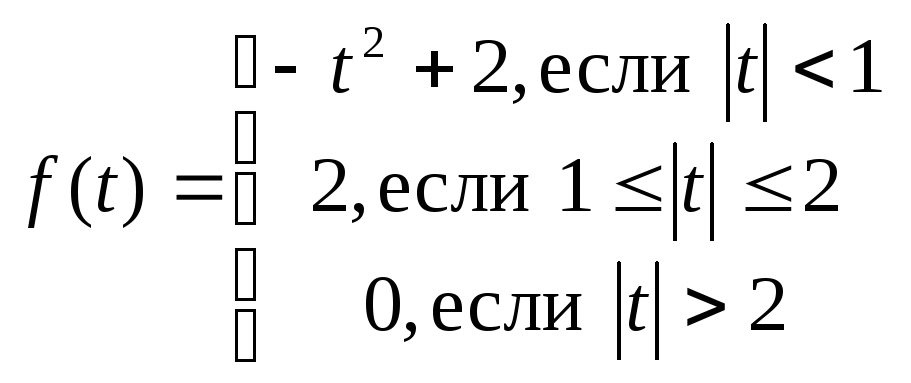5.7.
.
5.8.
.
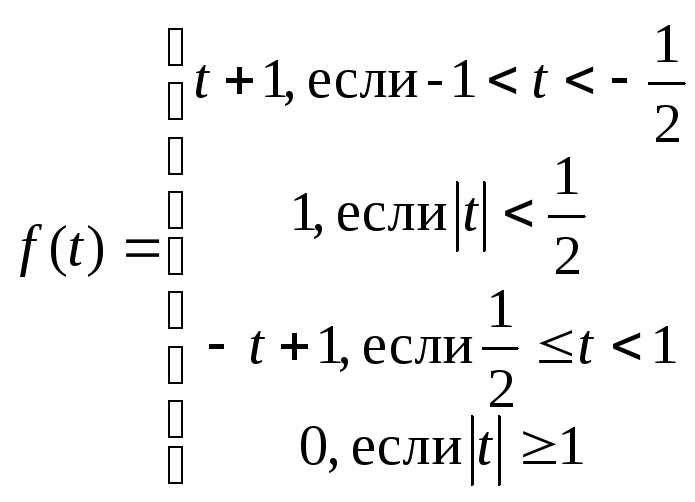5.9.
.
5.10.
.
5.11.
.
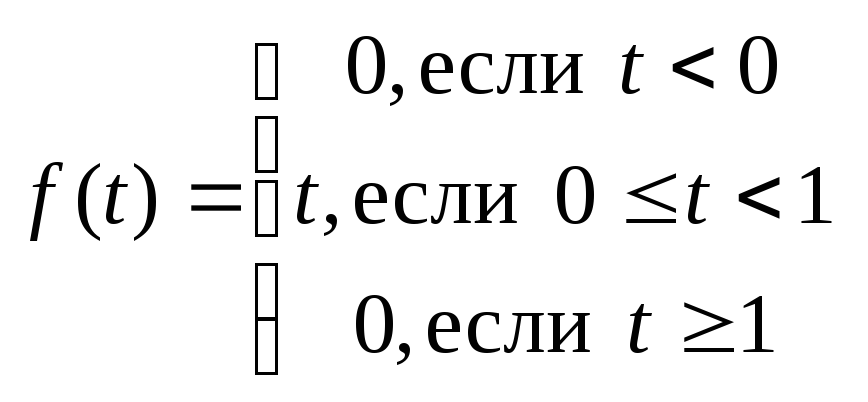5.12.
.
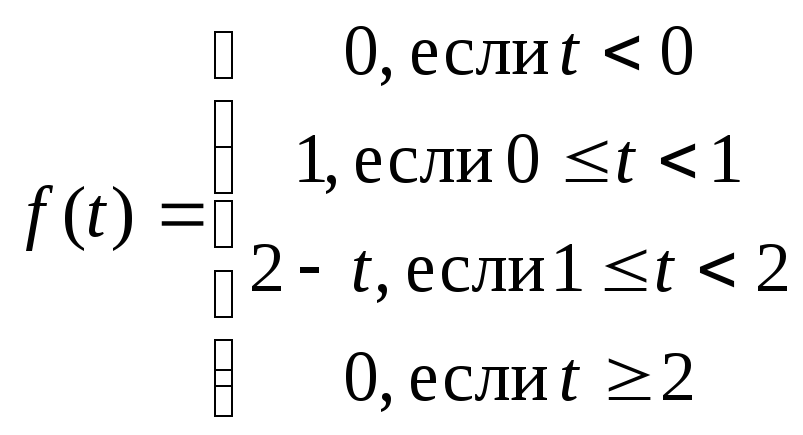5.13.
.
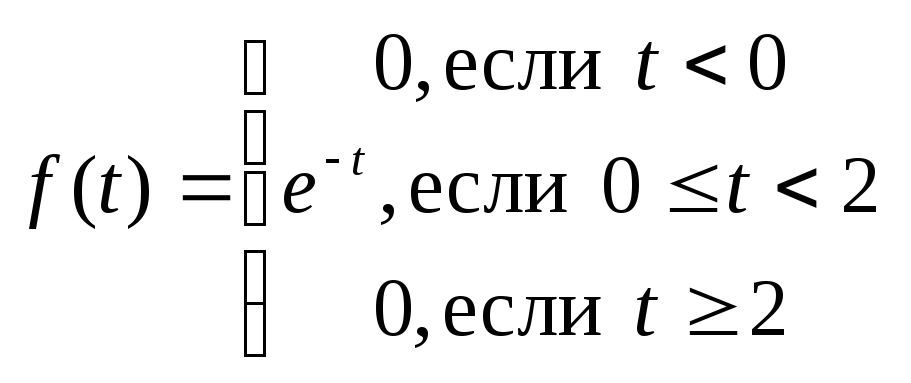5.14. f(t) = e-a | t | (a>0).
5.15. f(t) = te-a| t | (a>0).
5.16.
.
5.17.
.
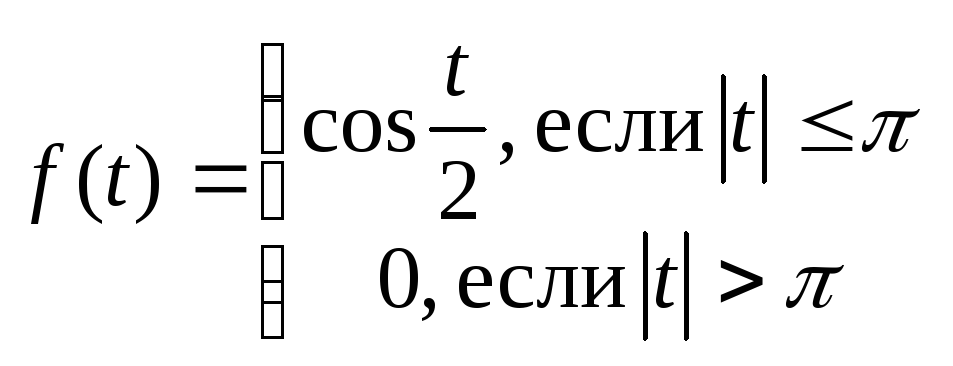5.18.
.
5.19.
.
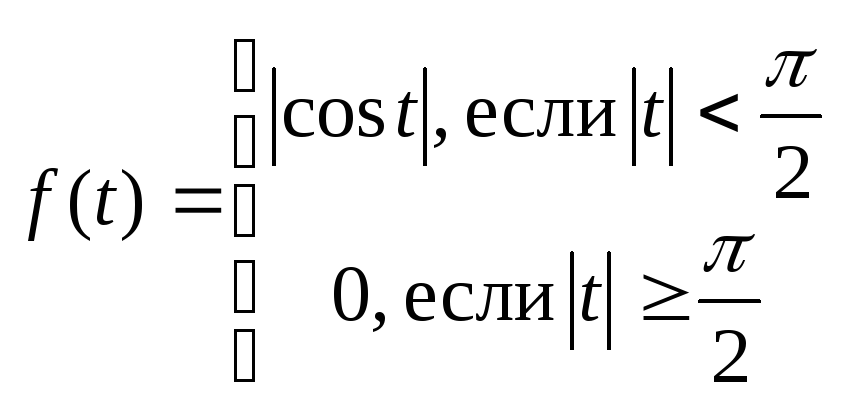5.20.
.
5.21.
5.22.
.
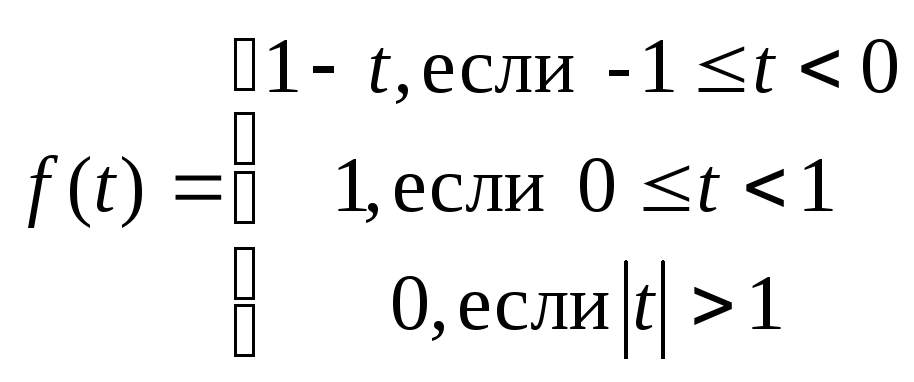5.23.
.
5.24.
.
5.25.
.
Задача 6.Найти область сходимости ряда.
6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
6.12.
6.13.
6.14.
6.15.
6.16.
6.17.
6.18.
6.19.
6.20.
6.21.
6.22.
6.23.
6.24.
6.25.
Задача 7.
Разложить функцию в ряд Тейлора по
степеням
.
7.1.
7.2.
7.3.
.
7.4.
.
7.5.
7.6.
7.7.
7.8.
.
7.9.
7.10.
7.11.
7.12.
7.13.
.
7.14.
.
7.15.
7.16.
7.17.
.
7.18.
.
7.19.
.
7.20.
7.21.
7.22.
.
7.23.
7.24.
7.25.
Задача 8. Вычислить интеграл с точностью до 0,001.
8.1.
8.2.
8.12.
8.13.
8.3.
8.4.
8.5.
8.6.
8.7.
8.8.
8.9.
8.10.
8.11.
8.14.
8.15.
8.16.
8.17.
8.18.
8.19.
8.20.
8.21.
8.22.
8.23.
8.25.
8.24.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Пискунов Н.С. Дифференциальное и интегральное исчисления. М., 1978. Т. 2. С. 326-366.
Романовский П. И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. М., 1964. С. 9-56.
Кожевников Н. И., Краснощекова Т.И., Шишкин Н.Е. Ряды и интеграл Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. М., 1964. С. 5-11, 28-34.
Гоноровский И.С. Радиотехнические цепи и сигналы. М., 1986. С. 31-39б 43-58.
Кузнецов Л.А. Сборник заданий по высшей математике. М., 2007.
ФУНКЦИОНАЛЬНЫЕ РЯДЫ