1. 2. Комплексная форма ряда Фурье

С помощью формул Эйлера

,

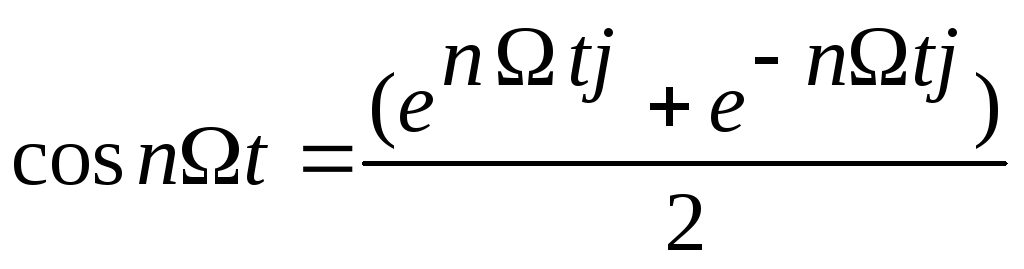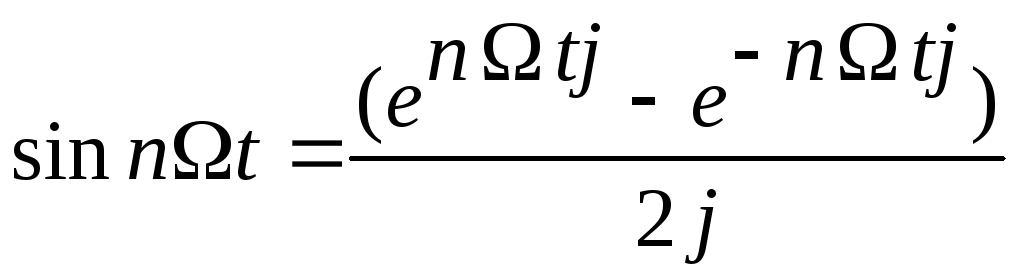
тригонометрический ряд (1) можно записать в комплексной форме

(8)

где

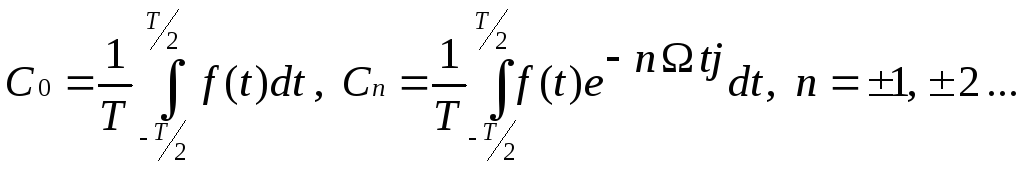(9)

Действительные и комплексные коэффициенты ряда Фурье связаны соотношениями:

(10)

Совокупность называется комплексным амплитудным спектром.

Пример 2. Сигнал представить рядом Фурье в комплексной форме. Воспользовавшись полученным разложением, записать ряд Фурье в действительной форме и построить графики спектров и .

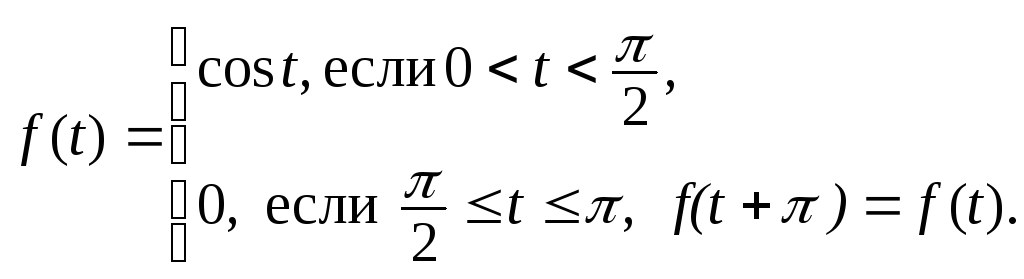
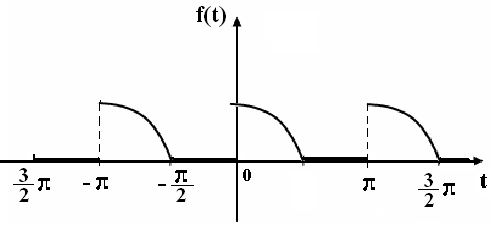
Рис. 4

Решение.

Вычислим коэффициенты ряда Фурье по формулам (9).

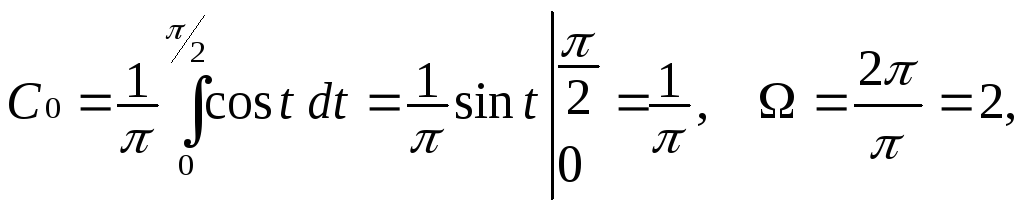
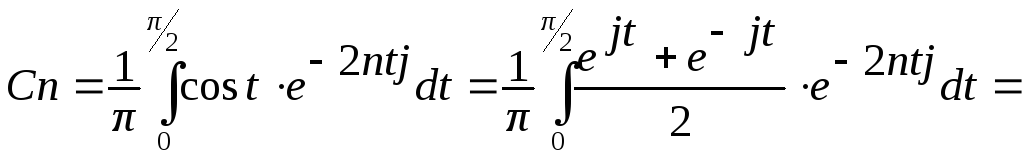
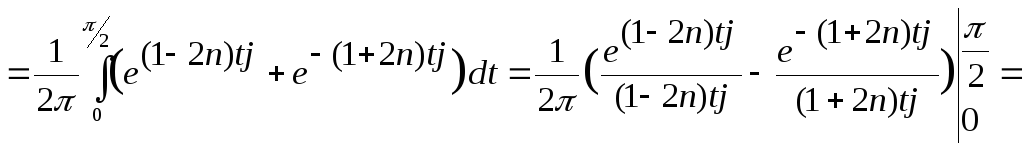
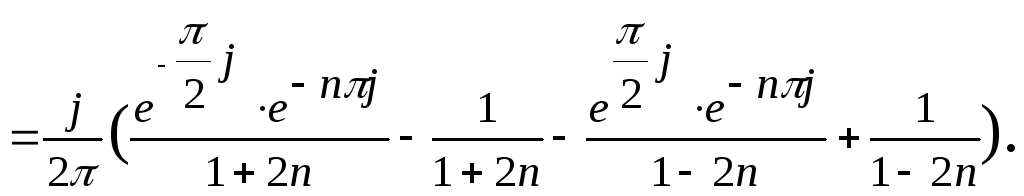
Применим формулы Эйлера:

Тогда

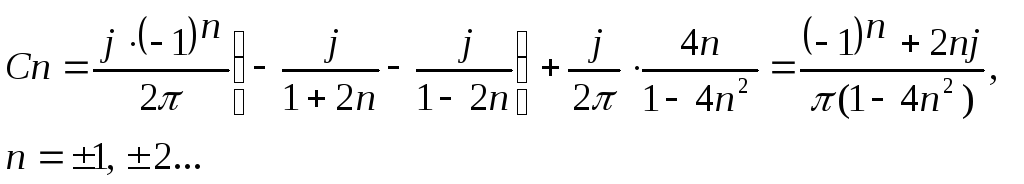
Следовательно, в точках непрерывности f(t) имеем (8):

Найдем коэффициенты тригонометрического ряда (10):

Подставляя эти коэффициенты в (1), получим:

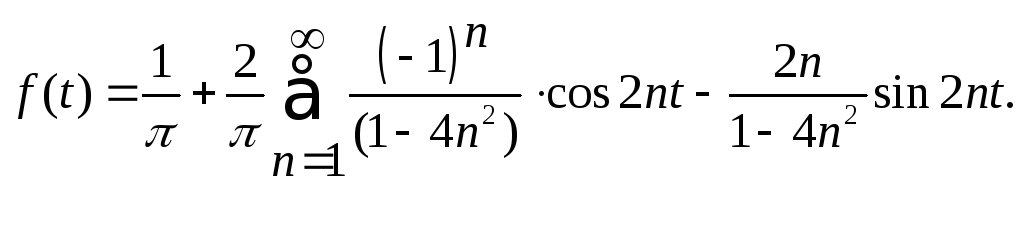
По формуле (7) вычислим амплитуды:

Графики амплитудных спектров имеют вид:

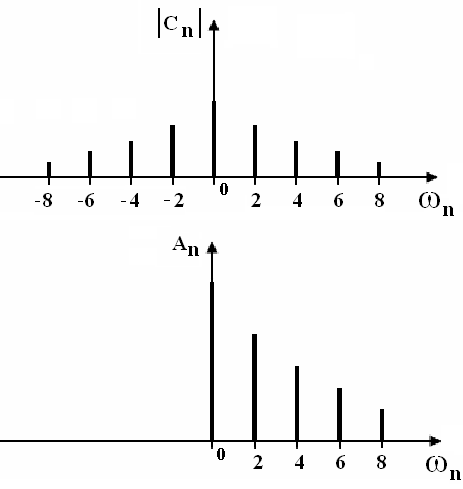
Рис. 5

1 .3. Разложение в ряд Фурье непериодических функций

Если функция f(t)задана на промежутке, то её следует доопределить так, чтобы она стала периодической, а затем вспомогательную функцию разложить в ряд Фурье. Поскольку вспомогательных функций, совпадающих сf(t)на, можно построить бесконечно много, то разложение не будет единственным. Если удастся доопределить функцию так, чтобы вспомогательная функция была чётной или нечётной то разложение упростится, так как ряд будет содержать в первом случае только косинусы, а во втором – только синусы (3). Но в любом случае навсе полученные ряды в точках непрерывности функции будут сходиться к заданной функцииf(t), а в точках разрыва – к среднему арифметическому пределов функции слева и справа.

Пример 3. Продолжая функцию f(t)четным образом, разложить в ряд Фурье по косинусам:

, если.

Решение. Введем вспомогательную функцию, φ(t), которая на отрезкесовпадает с функциейf(t)и является чётной и периодической (рис. 7):

.

t

Найдем коэффициенты ряда Фурье (3) для вспомогательной четной функции φ(t).

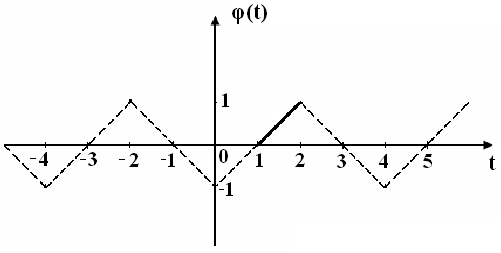
Рис. 7

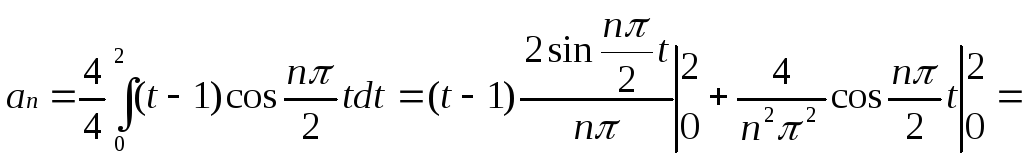
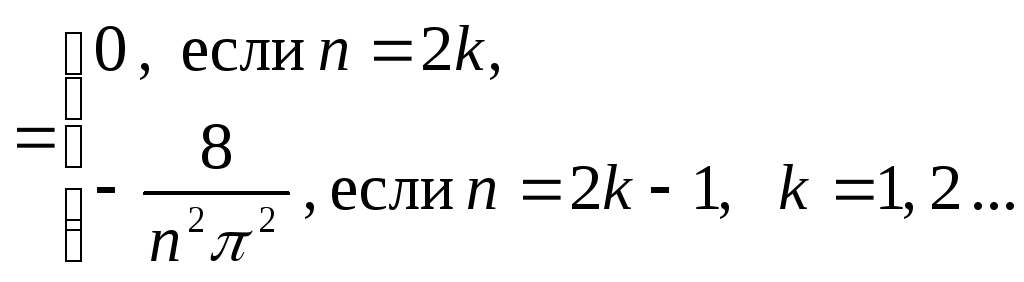
Тогда

На отрезке , следовательно, полученный ряд приявляется рядом Фурье для заданной функцииf(t).

1.4. Интеграл Фурье в действительной форме

Теорема. Пустьf(t)– абсолютно интегрируема на всей числовой оси, т.е, и на любом конечном интервалеразлагается в ряд Фурье. Тогда ее интеграл Фурье , где, (11)

равен f(t)в каждой точке непрерывности и равенв каждой точке разрыва функцииf(t).

В случае четной функции f(t)

нечетной

.

Таким образом, интеграл Фурье для четной функции имеет вид

, где.

Для нечетной

, где.

Функция называется косинус-преобразованием Фурье;- синус-преобразованием.

1.5. Интеграл Фурье в комплексной форме

Комплексная форма интеграла Фурье имеет вид

, (12)

где .(13)

Функция , определенная по формуле (13), называется преобразованием Фурье или спектральной плотностью.

Тогда по смыслу есть спектральная плотность амплитуд комплексного спектра.

Функция , определенная по формуле (12),называется обратным преобразованием Фурье. Напомним, что равенство (12) выполняется в точках непрерывности данной функции.

В математической литературе часто называют изображением, а- оригиналом и записываютили.