Работа № 3. Оценки

1. Cpавнение оценок

1.1. Определения

Пусть x₁, ..., x_n — выборка , т.е. n независимых испытаний случайной величины X , имеющeй функцию распределения F(x / a), зависящую от параметра a, значение которого неизвестно. требуется оценить значение параметра a.

Оценкой â = (x₁, ..., x_n) называется функция наблюдений, используемая для приближенного определения неизвестного параметра. Значение â оценки является случайной величиной, поскольку (x₁, ..., x_n) — случайная величина (многомерная).

Свойства оценок

1. Оценка â= (x₁, ..., x_n) называется состоятельной, если при n   â  a по вероятности при любом значении a.

2. Оценка â = (x₁, ..., x_n) называется несмещенной, если при любом a Mâ = M(x₁, ..., x_n) = a.

состоятельность - обязательное свойство используемых оценок. свойство несмещенности является желательным; многие применяемые оценки свойством несмещенности не обладают.

3. Оценка * называется оптимальной, если для неё средний квадрат ошибки

M(â- a)²= M[*(x₁, ..., x_n) - a]²= min M[(x₁, ..., x_n) - a]²

минимален среди всех оценок {}; здесь критерием качества оценки принят квадрат ошибки (â - a)². В более общей ситуации, если критерием качества служит некоторая величина L(â, a), называемая функцией потерь (или функцией штрафа), то оптимальная оценка та, для которой минимальна величина ML(â, a); последняя есть функциея неизвестного a и называется функцией условного риска. Ясно, что оптимальной оценки может не существовать (так как характеристикой является функция, а не число).

1.2. Постановка конкретной задачи.

Пример. Пусть на заводе имеется большая партия из N (тысячи) транзисторов, используемых для сборки некоторого прибора. Выходные параметры прибора (например, надежность, уровень шума, вероятность выхода из режима и т.д.) зависят от обратных токов транзисторов; обратный ток у разных экземпляров различен, и потому можно считать его случайной величиной, причем, как известно технологам, распределённой равномерно в диапазоне от 0 до I_max, где I_max —порог отбраковки, установленный на заводе - изготовителе транзисторов. Следовательно, выходные параметры прибора определяются величиной I_max. Предположим, что по каким-либо причинам значение I_max производителю приборов неизвестно. Ясно, что в этом случае из партии нужно случайным выбором извлечь n (сравнительно немного: десятки) транзисторов, измерить их ток, и по измерениям оценить I_max (неизвестный параметр а). Таким образом, возникает статистическая задача: по наблюдениям x₁, ..., x_n над случайной величиной , распределённой равномерно на отрезке [0, a], оценить неизвестный параметр a.

сравним три способа оценивания (три оценки):

оценку, полученную методом моментов,

â₁ = , (1)

оценку, полученную методом максимального правдоподобия (после исправления смещённости),

â₂ = max x_i (2)

и оценку, полученную методом порядковых статистик,

â₃ = 2 _0.5 = x_(k) + x_(k+1), (3)

где _0.5 =— выборочная квантиль порядка 0.5, т.е. выборочная медиана; x_(k) — член вариационного ряда с номером k; здесь полагаем n = 2k. Точность этих оценок можно сравнить теоретически и экспериментально (статистически).

Замечание. Точность, однако, не является единственным критерием качества оценок. Весьма важно, например, свойство устойчивости оценки к изменению закона распределения или к засорению; в этом смысле, как оказывается, â₃ — наиболее хороша, а â₂ — наименее; действительно, пусть, например, в нашу выборку случайно попало наблюдение, резко превосходящее все остальные (в случае с партией триодов, попался триод, не прошедший отбраковку); значение оценки â₂ резко изменится, значение â₃ почти не изменится.

1.3. Теоретическое сравнение оценок

Все три оценки несмещённые, что можно проверить методами теории вероятностей. определим дисперсии оценок :

Dâ₁ = D( ) = ,

Dâ₂ = D(max x_i ) = ,

Dâ₃ = D(x_(k) + x_(k+1)) ,

откуда ясно, что â₂ — наиболее точная оценка, а â₃ — наименее.

1.4. Статистическое сравнение оценок

Далеко не всегда удается аналитически вычислить дисперсию оценки. Как экспериментально определить, какой из оценок пользоваться? По одной выборке нельзя судить о разбросе значений оценки, поскольку значение всего одно; необходимо иметь несколько выборок, например, k = 20, (или хотя бы 5  10), оценить разброс значений для каждой оценки и предпочесть ту оценку (тот способ оценивания), для которой разброс меньше. Если же выборка всего одна, то следует (если n достаточно велико) разбить её случайным образом на несколько выборок, и по ним сравнивать качество оценок.

Сформируем k =20 выборок из распределения R[0, a=10] объема n для различных n=10, 40, 160 и определим разброс оценок. Характеристиками разброса значений а₁,...,а_k оценки â будем считать размах

w = max a_i - min a_i и среднеквадратичное отклонение (ско)

S_a= , .

Выполнение в пакете STATISTICA

Оценивание по выборкам объема n = 10

Шаг 1. Сформируем k =20 выборок объема n =10 и определим значения оценок a1, a2, a3 на каждой выборке. Создадим таблицу требуемых размеров (20v10c).

Шаг 2. Генерация выборок

Последовательность действий:

клавиша Vars - All specs... (спецификация всех) - появляется окно-таблица, в первом столбце которой находятся названия переменных (var1, var2,..., var20), а в Long Name - функция расчета. Выделим первую клетку этого столбца и введем = rnd(10)

 генерация случайных чисел, равномерно распределенных на отрезке [ 0, 10 ]. Скопируем эту запись в буфер обмена: Copy, а затем перенесем ее в остальные клетки (со 2 по 20) - ОК.

Далее нажмите кнопку x = ? - All variables - OK.

Шаг 3. Определим статистики, по которым вычисляются оценки. Выделим всю матрицу данных, затем найдем Sums (сумму), Max’s (максимальное) и Medians (медиану).В нижней части таблицы появляются 3 строки с требуемыми статистиками.

Для новых строк введем более удобные обозначения: Sumа, Maximum и Mediana, для этого дважды кликните по имени стоки.

Шаг 4. Транспонируем нашу матрицу, которая теперь имеет размер 20v13с в матрицу 13v  20c (чтобы совершать действия со столбцами): Data - Transponse - File.

Шаг 5. Вычислим значения оценок â₁, â₂ и â₃ на 20 выборках.

Добавим в матрицу 3 столбца (с 14 по 16 для значений оценок) Vars - Add - Number of vars: 3 - after: (после последней) и определим значения оценки â₁ - кн. Vars - Specs... (спецификация) - Name: A1 - Long name, согласно (1): = 2/10  Sumа

Аналогично определим значения оценок â₂ и â₃ ; различными будут операторы; для â₂ по (2): = 11/10  Maximum

для â₃ по (3): = 2  Medianа

Шаг 6. Сравнение оценок графически: Graphs - 2D Graphs - Line Plots (Variables) - в окне Variables: А1, A2, A3, Graphs Type : Multiple, - ОК.

Из графика видно, что значения оценок находятся в окрестности 10, и что оценка â₂ имеет разброс меньше, чем â₁ и â₃ .

Шаг 7. Определим характеристики разброса для оценок. Выделим столбцы a1, a2, a3 – и расчитаем для них- SD’s (стандартное отклонение), затем аналогично: Min’s, Max’s. (см. выше). Выписываем результаты в тетрадь и вычисляем размах w. Сравнение размахов w и стандартных отклонений S_а для трех оценок показывает, что оценка â₂(х₁, ... , х_n) наиболее точна, а оценка â₃(х₁, ... , х_n) - наименее.

Задание

Проведите оценивание по выборкам объема n=40 и n=160 и итоговое сравнение аналитически и графически.

Заролните следующую табдицу.

Таблица 1. Разброс значений оценок.

		â1	â2	â3
	amin
n = 10	amax
	w
	Sa
	amin
n = 40	amax
	w
	Sa
	amin
n = 160	amax
	w
	sa

Убедитесь в том, что приведенные результаты экспериментального сравнения 3 способов обработки наблюдений показывают следующее:

1. Значения оценок концентрируются в окрестности оцениваемого параметра (проявление свойства несмещенности оценок).

2. С ростом числа наблюдений точность (величина разброса) оценок улучшается (проявление свойства состоятельности).

3. Различные оценки различаются по величине средней ошибки, откуда ясно, что различные способы обработки наблюдений нужно сравнивать по величине среднего значения некоторого критерия качества, например, среднего значения квадрата ошибки.

Работа N4. Доверительные границы и интервалы

результатом применения точечной оценки â(x₁,...,x_n) является одно числовое значение; оно не дает представления о точности, т.е. о том, насколько близко полученное значение к истинному значению параметра. Интуитивно ясно, что такое представление может дать, например, дисперсия оценки, так что истинное значение должно находиться где-то в пределах

â  (24)

Внесем уточнения.

Основные положения

Определения и построение интервалов.

Пусть (x₁,...,x_n)  x - n независимых наблюдений над случайной величиной с законом распределения F(z/a), зависящим от параметра a, значение которого неизвестно.

Определение 1. Функция наблюдений a₁(x₁,...,x_n) (заметим, что это случайная величина) называется нижней доверительной границей для параметра a с уровнем доверия Р_Д (обычно близким к 1), если при любом значении

P{ a₁(x₁,...,x_n) a}  P_Д

Определение 2. Функция наблюдений a₂(x₁,...,x_n) (случайная величина) называется верхней доверительной границей для параметра с уровнем доверия Р_Д , если при любом значении

P{ a₂(x₁,...,x_n)  a }  P_Д .

Определение 3. Интервал со случайными концами (случайный интервал)

I(x) = ( a₁(x), a₂(x) ) ,

определяемый двумя функциями наблюдений, называется доверительным интервалом для параметра a с уровнем доверия Р_Д , если при любом значении a

P{ I(x) a }  P{ a₁(x₁,...,x_n)  a  a₂(x₁,...,x_n) }  P_Д ,

т.е. вероятность (зависящая от a) накрыть случайным интервалом I(x) истинное значение a - велика: больше или равна Р_Д.

Построение доверительных границ и интервалов.

Для построения доверительного интервала (или границы) необходимо знать закон распределения статистики =(x₁,...,x_n), по которой оценивается неизвестный параметр (такой статистикой может быть оценка  = â(x₁,...,x_n) ). Один из способов построения состоит в следующем. Предположим, что некоторая случайная величина  = (, a), зависящая от статистики  и неизвестного параметра a такова, что

1) закон распределения известен и не зависит от a;

2) (, a) непрерывна и монотонна по .

Выберем диапазон для  интервал так, чтобы попадание в него было практически достоверно:

P{ f₁  (, a)  f₂ }  P_Д , (1)

для чего достаточно в качестве ивзять квантили распределенияуровня (1- Р_Д )/2 и (1+ Р_Д )/2 соответственно. Перейдем в (1) к другой записи случайного события, разрешив неравенства относительно параметра a; получим (полагая, что монотонно возрастает по):

P{ g(, f₁)  a  g(, f₂) }  P_Д .

Это соотношение верно при любом значении параметра a (поскольку это так для (1)), и потому, согласно определению, случайный интервал

( g(, f₁) , g(, f₂) )

является доверительным для a с уровнем доверия Р_Д . Если убывает по, интервалом является (g(, f₂) , g(, f₁) ).

Для построения односторонней границы для a выберем значения итак, чтобы

P{ (, a)  f₁ }  P_Д , f₁=Q(1 - P_Д )

или P{ (, a)  f₂ }  P_Д , f₂ = Q( P_Д ),

где  квантиль уровня . После разрешения неравенства под знакомполучим односторонние доверительные границы для a.

Пример. Доверительный интервал с уровнем доверия Р_Д для среднего a нормальной совокупности при известной дисперсии .

Пусть x, ... , x_n - выборка из нормальной N(a, ) совокупности. Достаточной оценкой для а является

â = â(x,...,x_n) = ,

распределенная по закону N(a, ) ; пронормируем её, образовав случайную величину

, (2)

которая распределена нормально N(0,1) при любом значении а.

По заданному уровню доверия Р_Д определим для  отрезок -f_p, f_p так, чтобы

, (3)

т.е. f_p - квантиль порядка (1+ Р_Д )/2 распределения N(0,1); заметим, что  зависит от а , но (3) верно при любом значении а. Подставим в (3) выражение для  из (2) и разрешим неравенство под знаком вероятности в (3) относительно а ; получим соотношение

, (4)

верное при любом значении а. под знаком вероятности две функции наблюдений

, (5)

определяют случайный интервал

I( x₁, ... , x_n) =(a₁( x₁, ... , x_n), a₂( x₁, ... , x_n)), (5a)

который в силу (4) обладает тем свойством , что накрывает неизвестное значение параметра а с большой вероятностью Р_Д при любом значении а, и потому, по определению доверительно интервала, он является доверительным с уровнем доверия Р_Д .

В общем случае случайную величину  в (1) можно построить следующим образом. Определим функцию распределения F(z/a) статистики  (F, конечно, зависит от а). Для непрерывной  случайная величина (, а) F( /a), как нетрудно видеть, распределена равномерно на отрезке 0, 1 при любом значении а; приняв f₁= (1- P_Д)/2, f₂ =(1+P_Д)/2, будем иметь в качестве (4)

P{f₁  F( /a)  f₂} = P_Д .

Для дискретной  ситуация аналогична.

Можно рассуждать иначе: при любом фиксированном значении а определим отрезок z₁(a), z₂(a)  так, что

P{ z₁(a)    z₂(a) }  Р_Д ; (6)

ясно, что в качестве z₁ и z₂ можно взять квантили, т.е. определить из условий

F(z₁/a)=(1- Р_Д )/2, F(z₂/a)=(1+ Р_Д )/2.

Если z₁(a) и z₂(a) монотонно возрастают по а, то, разрешив два неравенства под знаком Р в (6) и учитывая, что z₁(a) < z₂(a), получим:

P{ z₂^-1()  a  z₁^-1() }  Р_{Д ,}

вверное при любом а; ясно, что интервал ( z₂^-1() , z₁^-1() ), определяемый двумя функциями от  , является доверительным с уровнем доверия Р_Д.

Уровень доверия

Уровень доверия Р_Д означает, что правило определения интервала дает верный результат с вероятностью Р_Д, которая обычно выбирается близкой к 1, однако, 1 не равно. Убедимся статистически на примере в том, что доверительный интервал с уровнем доверия Р_Д может не содержать (с малой вероятностью 1- Р_Д ) истинное значение параметра.

Пример. рассмотрим приведенный в (5) случайный интервал I(x₁, ..., x_n), который при любом значении а накрывает это значение с большой вероятностью Р_Д:

Р{ I(x₁,...,x_n)  a } = Р_Д ,

и потому, если пренебречь возможностью осуществления события aI, имеющего малую вероятность (1-Р_Д), можно считать событие aI(x₁,...,x_n) практически достоверным, т.е. можно верить тому, что вычисленный по конкретным наблюдениям x₁,...,x_n интервал I содержит неизвестное значение параметра а.

Испытаем интервал (5) на 50 выборках объема n=10 для трех уровней доверия Р_Д : 0.9 , 0.99 , 0.999 (соответственно, три значения f_p) .

При Р_Д = 0.9 число неверных из k =50 результатов окажется в окрестности 5, так как среднее число неверных

k(1- Р_Д) = 5;

при Р_Д =0.99 появление хотя бы одного неверного из k =50 весьма вероятно: вероятность этого события

1- Р_Д^k=1-0.99⁵⁰  0.61;

при Р_Д =0.999 появление хотя бы одного неверного весьма сомнительно: вероятность этого события

1- Р_Д^k=1-0.999⁵⁰  0.05.

Задание.

1. Определить, сколько раз из k =50 доверительный интервал оказался неверным, это сделаем для трех значений Р_Д . Графики для Р_Д =0.9 и Р_Д =0.99 распечатать. Выполнение в пакетах см. в пп. 2 - 4.

2. Провести аналогично 50 испытаний доверительного интервала (7) - (9) для случая неизвестной дисперсии.

Интервалы для параметров нормального распределения

Пусть х₁, … ,х_n - выборка из нормального N(a,²) распределения; значения среднего а и дисперсии ² неизвестны. Оценки для а и ²:

, . (7)

Как известно, доверительным интервалом для среднего а с уровнем доверия Р_Д при неизвестной дисперсии является интервал

I(x) = (a₁(х), a₂(х) ), (8)

где ,, (9)t_p - квантиль порядка (1+ Р_Д)/2 распределения Стьюдента с n-1 степенями свободы.

Доверительным интервалом для стандартного отклонения  с уровнем доверия Р_Д является интервал

I (x)=(₁(х), ₂(х)) , (10)

где ,, (11)

t₁ и t₂- квантили порядков соответственно (1+ Р_Д)/2 и (1- Р_Д)/2 распределения хи-квадрат с n-1 степенями свободы.

Сгенерируем выборку объема n=20 из нормального распределения с параметрами a =10, ²=2²=4 и определим доверительные интервалы для a и  с уровнем доверия Р_Д : 0.8 , 0.9 , 0.95 , 0.98 , 0.99 , 0.995 , 0.998 , 0.999. Результаты выпишем в виде таблицы. C ростом Р_Д интервал расширяется, с ростом n - уменьшается.

Выполнение см. в пп. 2 - 4.

Если нас интересуют не интервалы, а верхние или нижние доверительные границы, то, как известно, они определяются теми же формулами (9) è (11), однако, значения порогов t изменяются. Например, нижней доверительной границей для a с уровнем доверия Р_Д является значение

,

где t_p - квантиль порядка Р_Д распределения Стьюдента с n-1 степенями свободы, а верхней границей для  с уровнем доверия Р_Д является

,

где t₂ - квантиль порядка 1- Р_Д распределения хи-квадрат с n-1 степенями свободы.

Задание: определить верхние доверительные границы для а и  с уровнем доверия Р_Д = 0.95 .

Задание на самостоятельную работу

1) для заданной задачи построить оценку заданным методом (варианты заданий см. ниже);

2) построить доверительный интервал, основанный на этой оценке;

3) сгенерировать выборку заданного объема;

4) вычислить доверительный интервал.

Отчет по работе должен содержать:

постановки вопросов, формулы,

графики испытания доверительного интервала для 2-х случаев: с известной и неизвестной дисперсией (по п. 1.2),

таблицу доверительных интервалов для различных Р_Д (по п. 1.3),

вывод формул для оценок и интервалов, сгенерированную выборку и вычисленный интервал (по п. 1.4) .

Варианты задач.

Задача1. Расстояние а до некоторого объекта измерялось n₁ раз одним прибором и n₂- вторым; результаты х₁,…,х_n1; y₁,…,y_n2. Оба прибора при каждом измерении дают независимые случайные ошибки, нормально распределенные со средним 0 и стандартными отклонениями ₁ и ₂ соответственно. Методом максимального правдоподобия построить оценку â для а и доверительный интервал с уровнем доверия Р_Д .

Варианты исходных данных

¹	n1	n2	1, êì	2, êì	Ðä	a, êì
1	5	10	3	5	0.95	300
2	8	12	3	5	0.98	300
3	10	15	3	5	0.95	300
4	5	10	4	6	0.98	350
5	8	12	4	6	0.95	350
6	10	15	4	6	0.98	350
7	5	10	5	8	0.95	400
8	8	12	5	8	0.98	400
9	10	15	5	8	0.95	400

измерения получить моделированием с заданным параметром а.

Решение (без вывода). Оценка

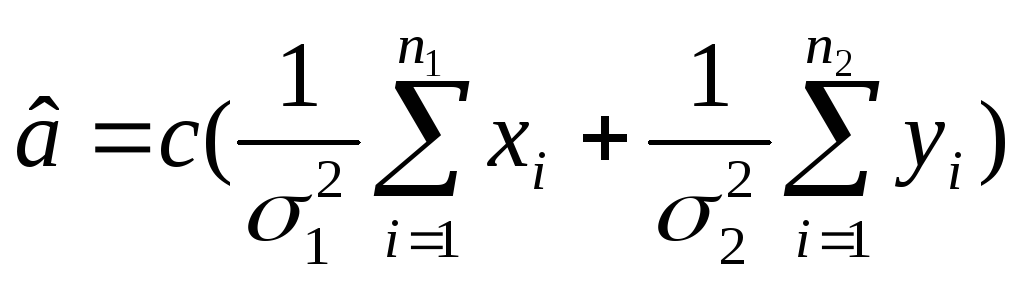, где с=;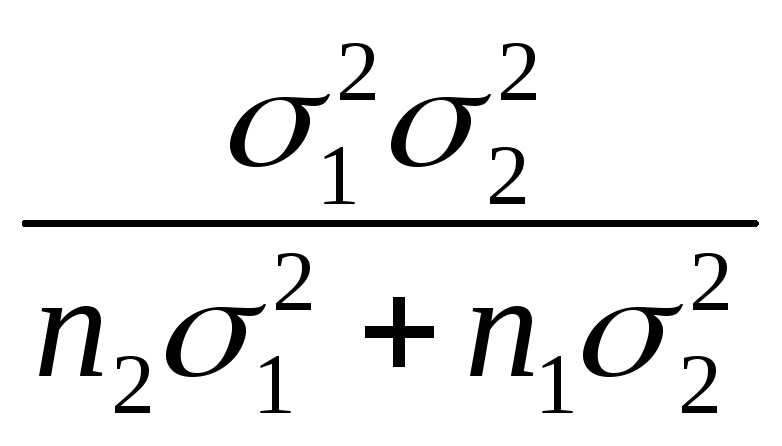

доверительный интервал

I=(,),

где - квантиль порядка (1+Р_Д)/2 распределения N(0,1).

Задача 2. Изготовлена большая партия из N=10000 приборов. Известно, что время безотказной работы случайно и распределено по показательному закону с плотностью

, x  0

С целью определения значения параметра а этой партии были поставлены на испытания n приборов; времена безотказной работы оказались равными х₁,…,х_n. Методом моментов построить оценку для а и доверительный интервал с уровнем доверия Р_Д . Кроме того, построить доверительный интервал для числа М приборов, имеющих время безотказной работы менее 50 часов.

Варианты исходных данных

	1	2	3	4	5	6	7	8	9
n	20	25	30	20	25	30	20	25	30
ÐД	0.95	0.99	0.95	0.99	0.95	0.99	0.95	0.99	0.95
à	300	400	500	300	400	500	300	400	500

измерения получить моделированием с заданным параметром а.

Решение (без вывода). Оценка

;

доверительный интервал для а

I_a = (, ),

где t₁=Q(2n, (1-Р_Д)/2), t₂=Q(2n, (1+Р_Д)/2) - квантили распределения хи-квадрат с 2n степенями свободы; доверительный интервал для М

I_M = ( N(1- exp(-)), N(1- exp(-)) ).

Задача 3. Некоторое неизвестное расстояние а измерялось с аддитивной случайной ошибкой  , распределенной по закону Коши с плотностью

p_( x ) = , -  < x < .

По результатам х₁,…,х_n независимых измерений методом порядковых статистик построить оценку для а и приближенный доверительный интервал с коэффициентом доверия Р_Д .

Варианты исходных данных

	1	2	3	4	5	6	7	8	9
n	30	40	50	30	40	50	30	40	50
b	3	4	5	6	3	4	5	6	3
ÐД	0.95	0.98	0.95	0.98	0.96	0.98	0.95	0.98	0.95
a	15	20	25	15	20	25	15	20	25

измерения получить моделированием с заданным параметром а.

Решение (без вывода).Оценкой для а является выборочная медиана - порядковая статистика с номером [n/2]+1

,

или

(у этих статистик асимптотические свойства одинаковы). Приближенный доверительный интервал, основанный на асимптотическом распределении выборочной р-квантили

I=(),

где t_p=Q((1+Р_Д)/2) - квантиль порядка (1+Р_Д)/2 распределения N(0,1).

Задача 4. В водоеме обитает некоторая биологическая популяция, состоящая из смеси особей двух возрастов. Длина особи - случайная величина, распределенная по нормальному закону N( a_i, _i² ), где i=1,2 - индекс, относящийся к возрасту. С целью определения доли q особей 1-го возраста проведен отлов n особей и измерена их длина. По результатам х₁,…,х_n методом моментов построить оценкудляq и приближенный доверительный интервал с уровнем доверия Р_Д . Построить гистограмму наблюдений.

Варианты исходных данных

	1	2	3	4	5	6	7	8	9
n	40	50	60	40	50	60	40	50	60
à1	5	6	5	6	5	6	5	6	5
à2	8	9	8	9	8	9	8	9	8
ÐÄ	0.95	0.95	0.98	0.95	0.95	0.98	0.95	0.95	0.98
q	0.5	0.4	0.3	0.5	0.4	0.3	0.5	0.4	0.3

Принять ₁=1см, ₂=1см. измерения получить моделированием с заданным значением q.

Решение (без вывода):

I = ( q₁, q₂ ),

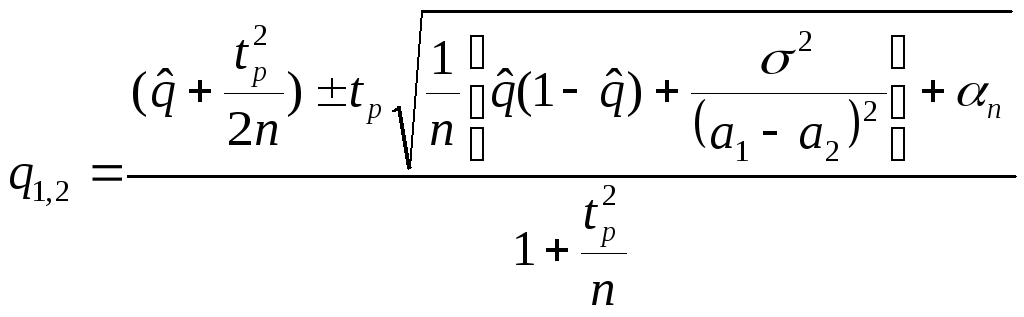, _n  ,

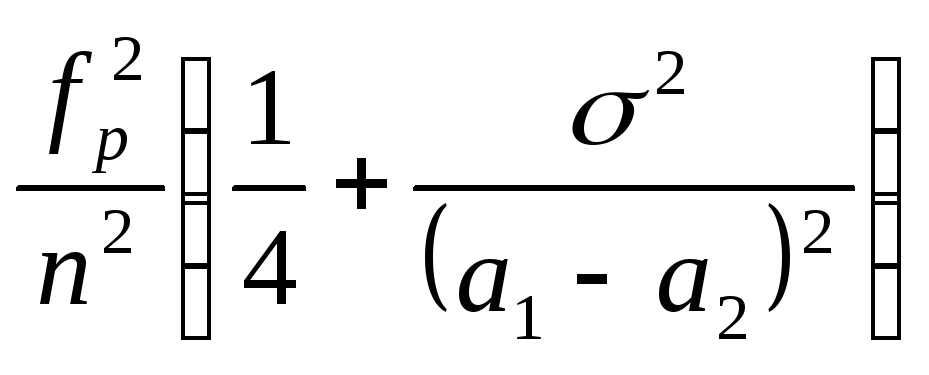t_p- квантиль порядка (1+ Р_Д)/2 для N(0,1).