Фазовые портреты динамических систем

Модели, представленные одним дифференциальным уравнением первого порядка (17) не могут описывать реальные процессы, часто имеющие колебательный характер. Такую возможность представляют системы дифференциальных уравнений более высокого порядка. Хорошие результаты получаются при использовании системы двух уравнений первого порядка, допускающей исследование переменных на фазовой плоскости. Остановимся на некоторых общих свойствах таких систем, описываемых в общем виде уравнениями

dx	= P(x, y);	dy	= Q(x, y) (18)
dt		dt

( )

г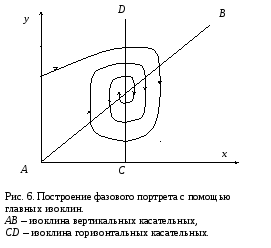деP(x, y) и Q(x, y) – непрерывные функции, определенные в некоторой области G евклидовой плоскости (х, у – декартовы координаты) и имеющие в этой области непрерывные производные не ниже первого порядка.

Область может быть как неограниченной, так и ограниченной. Биологические или химические переменные не могут быть отрицательными величинами, поэтому область представляет собой положительный квадрант правой полуплоскости:

0 ≤ х ≤ ∞, 0 ≤ у ≤ ∞.

Часто численное значение переменных может быть ограничено внешними условиями, тогда они могут быть ограничены и снизу и сверху:

х₁₀ ≤ х ≤ х₂₀; у₁₀ ≤ у ≤ у₂₀.

К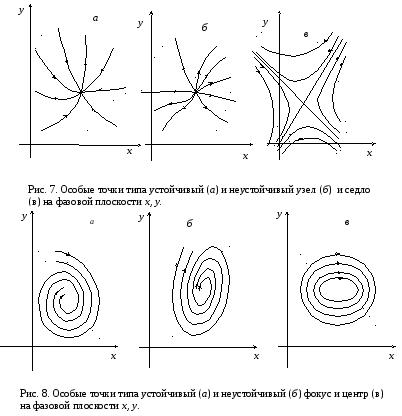аждому состоянию системы соответствует пара значений переменныхх и у. На фазовой плоскости с осями координат х, у каждая точка М (х, у) соответствует определенному состоянию системы. Эта точка называется изображающей или представляющей. Пусть при t = t₀ координаты изображающей точки будут М₀(х₀, у₀), тогда в каждый последующий момент изображающая точка будет смещаться и принимать положение М(х, у), соответствующее значениям x(t), y(t), образуя фазовую траекторию. Совокупность фазовых траекторий образует фазовый портрет.

Чтобы построить фазовый потрет системы необходимо построить векторное поле направлений траекторий системы в каждой точке плоскости х, у. Это сложная задача, поэтому используют качественный подход – так называемый метод изоклин. Метод заключается в том, что на фазовой плоскости наносятся линии, которые пересекают интегральные кривые под одним определенным углом. Часто ограничиваются построением главных изоклин: dy/dx = 0 - изоклина горизонтальных касательных к фазовым траекториям, уравнение которой Q(x, y) = 0 и изоклина вертикальных касательных dy/dx = ∞, которой соответствует уравнение P(x, y) = 0.

Точки пересечения главных изоклин представляют собой особые точки, в которых направление касательных к интегральным кривым неопределенно.

Так как решение системы (18) зависит от начальных условий, то иногда, чтобы подчеркнуть это обстоятельство решение записывается

x =φ(t – t_o, x_o, y_o); y =ψ(t – t_o, x_o, y_o)

Решение системы уравнений (2) с заданными х₀, у₀, t₀, можно рассматривать как параметрическое уравнение некоторой кривой на фазовой плоскости х, у со временем t в виде параметра. Ясно, что каждая фазовая траектория у = у(х) является проекцией на фазовую плоскость х, у некоторой интегральной кривой в пространстве х, у, t.

Согласно теореме Коши интегральные кривые в пространстве х, у, t и фазовые траектории в плоскости х, у не должны пересекаться. Достижение состояний равновесия происходит только асимптотически при t → ∞. Состояние равновесия х = *х устойчиво по Ляпунову если в момент времени t₀ отклонение от состояния равновесия мало

|x(t₀) -*x| < ξ , |у(t₀) -*у| < ξ

то в любой последующий момент времени t ≥ t₀ отклонение от состояния равновесия будет также мало

|x(t) -*x| < ε, |у(t) -*у| < ε.

Рассмотрим простейшую динамическую систему, представленную двумя линейными дифференциальными уравнениями первого порядка:

dx	=ax + by
dt

(19)

dy	= cx + dy
dt

где a, b, c, d – константы, а х, у – декартовы координаты на фазовой плоскости.

Общее решение системы будем искать в виде

x = Ae^λt, y = Be^λt

Подставим эти выражения в (19) и сократим полученные выражения на e^λt:

λA = aA + bB,

(20)

λB = cA + dB

Эта система уравнений с неизвестными А, В имеет ненулевое решение, если определитель, составленный из коэффициентов при неизвестных равен нулю:

a – λ b	= 0
c d – λ

Раскроем этот определитель и решим полученное характеристическое уравнение

λ² – (a+d)λ +(ad – bc)= 0 (21)

Решение этого уравнения дает значения показателя λ_1,2 при которых возможны ненулевые для А и В решения системы (20):

λ_1,2 = ½(a + d) ± √¼(a + d)² + (bc – ad)

Тогда общее решение системы (19) можно представить в виде линейной комбинации экспонент с показателями λ₁ и λ₂:

y = c₁₁e ^λ1t + c₁₂e^λ2t

x = c₂₁e ^λ1t + c₂₂e^λ2t

В случае отсутствия вырождения, т. е. ad – bc ≠ 0 возможно шесть типов состояний равновесия в зависимости от свойств корней характеристического уравнения (Рис. 7, 8):

1) устойчивый узел (λ₁ и λ₂ действительны и отрицательны);

2) неустойчивый узел (λ₁ и λ₂ действительны и положительны);

3) седло (λ₁ и λ₂ действительны и разных знаков);

4) устойчивый фокус (λ₁ и λ₂ комплексны и Reλ<0);

5) неустойчивый фокус (λ₁ и λ₂ комплексны и Reλ>0);

6) центр (λ₁ и λ₂ мнимые).