9

Качественный анализ динамических систем

Важнейшим свойством открытых систем является установление в них стационарных состояний, в отличие от термодинамического равновесия. Интерес вызывают следующие вопросы: а) существуют ли в системе стационарные состояния и сколько их; б) какова их устойчивость и как устойчивость зависит от параметров системы; в) как ведет себя система вблизи стационарных состояний, возможны ли между ними переходы. Изучением этих вопросов занимается качественная теория дифференциальных уравнений. Этот подход наиболее эффективен при наличии системы автономных дифференциальных уравнений вида (7). Состояние такой системы в п-мерном пространстве будет описываться точкой в этом пространстве

М = М(х₁, х₂, … х_п);

в стационарном состоянии –

*М = *М(*х₁, *х₂, … *х_п).

Пространство с координатами х₁, х₂, … х_п называется фазовым, кривая, описываемая точкой М – фазовой траекторией.

Рассмотрим простейшую математическую модель, которой соответствует дифференциальное уравнение 1-го порядка:

dх	= f(х) (17)
dt

Состояние таких систем в каждый момент времени характеризуется одной величиной х в данный момент времени t. Если для уравнения (17) выполнены условия теоремы Коши, то есть f(х) является аналитической на некотором заданном интервале, то имеется единственное решение, удовлетворяющее начальным условиям и через точку х, t, проходит одна единственная кривая х(t).

Пусть уравнение (17) имеет действительные корни *х₁,* х₂,* х₃. На плоскости t, х это прямые, параллельные t и пересекающие ось х в точках *х₁,* х₂,*х₃. Они разбивают плоскость t, х на ряд полос (Рис. 4). Так как интегральные кривые не могут пересекаться (в силу теоремы Коши), то каждая интегральная кривая должна целиком заключаться в одной из таких полос и быть монотонной, так как внутри полосы f(х) не меняет знака. Зная свойства функции f(х) можно выяснить характер кривых на плоскости t, х.

П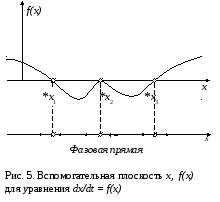оведение исследуемой системы, выраженное уравнением (1) можно охарактеризовать положением изображающей точки на фазовой прямойх (Рис.5) В силу теоремы Коши, задание начального значения х = х₀ в начальный момент времени t = t₀ однозначно определит дальнейшее движение изображающей точки вдоль фазовой прямой во времени.

На фазовой прямой х траектории (направления) движения изображающей точки зависят от знака f(x) = dx/dt. Если f(x)>0, то изображающая точка движется вправо; если f(x)<0, движение направлено влево; точки, где f(x) = 0 соответствуют состояниям равновесия.

Таким образом, поведение интегральных кривых на плоскости t, х можно установить, не решая в явном виде дифференциального уравнения, если известен характер движения изображающей точки на фазовой прямой.

Устойчивость динамических систем

Рассмотрим критерии устойчивости состояний равновесия. Если при достаточно малом начальном отклонении от положения равновесия система никогда не уйдет далеко от особой точки, то особая точка является устойчивым состоянием равновесия и соответствует устойчивому стационарному режиму функционирования системы. Иными словами, состояние равновесия устойчиво, если достаточно малое возмущение всегда остается малым.

Состояние равновесия х =*х устойчиво по Ляпунову если в момент времени t₀ отклонение от состояния равновесия мало

|x(t₀) -*x| < ξ ,

то в любой последующий момент времени t ≥ t₀ отклонение от состояния равновесия будет также мало

|x(t) -*x| < ε.

Пусть наша система отклонилась от точки равновесия*х и перешла в соседнюю с ней точку х. Положим х = *х+ξ, где ξ – малое отклонение от состояния равновесия, такое, что 1/ξ << 1. По нашему предположению f(х) – аналитическая функция. Перейдем от переменной х к переменной ξ в уравнении (17), подставив туда х = *х+ξ. Получим

d(*х+ξ)	=	dξ	= f(*х+ξ)
dt		dt

Стоящую в правой части этого уравнению функцию разложим в ряд Тейлора в точке *х:

dξ/dt = f(*x) + f ^׳(*x)ξ + ½f ^״ξ² + …

Проведем линеаризацию этого выражения, отбросив в этом уравнении нелинейные члены как величины более высокого порядка малости. В результате получим линейное уравнение

dξ	= λξ
dt

где λ = f ^׳(*x). Тогда

ξ(t) = Ce^λt, C = const.

Если λ < 0, то при t → ∞ ξ → 0, а следовательно, первоначальное отклонение ξ от равновесия со временем самопроизвольно затухает. Таким образом, стационарное решение х = *х устойчиво по Ляпунову. Наоборот, если λ > 0, то при t → ∞ ξ → ∞ и исходное состояние неустойчиво. Если λ = 0, то ситуация является неопределенной. Таким образом, по знаку производной f ^׳(*x) можно сделать вывод об устойчивости особых точек.

Например, уравнение логистической кривой для численности популяции

dN	= Nr	Nmax – N
dt		Nmax

имеет два корня *х₁ = 0 и *х₂ = N_max . Подставляя эти значения в выражение производной

f ^׳(x)|_{х =*х} = r – 2r*x/N_max,

можно сделать вывод об устойчивости особых точек. Так, при *х₁ = 0 f ^׳(x) = r > 0, следовательно, *х₁ = 0 является неустойчивой особой точкой. Если *х₂ = N_max, то f ^׳(x) = − r < 0, то эта особая точка является устойчивой по Ляпунову.

Для более сложных динамических систем можно применить следующие закономерности, вытекающие из предыдущих рассуждений:

• если вблизи состояния равновесия х = *х функция f(x) меняет свой знак с плюса на минус при возрастании х, то такое состояние является устойчивым;

• если вблизи состояния равновесия х = *х функция f(x) меняет свой знак с минуса на плюс при возрастании х, то такое состояние является неустойчивым;

• если в окрестностях особой точки *х функция f(x) не меняет своего знака при возрастании х, то в этом случае состояние равновесия также является неустойчивым.